Motor Power Factor Correction

Electricity and Magnetism Level 3

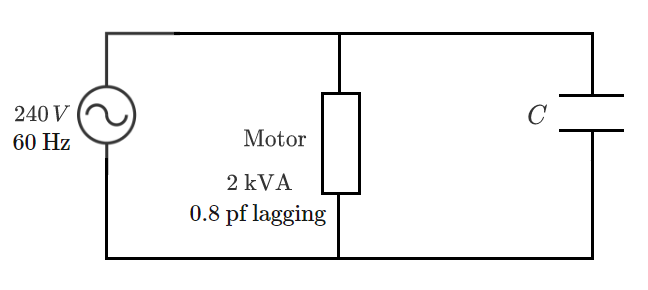
An ideal AC voltage source supplies an induction motor load in a residential application. How many microfarads $(\mu F)$ of capacitance should be connected in parallel with the motor in order to correct the load's overall power factor to unity?

Note: The source voltage magnitude is in RMS. "pf" stands for "power factor". The $2 \, \text{kVA}$ number is the apparent power drawn by the motor.

The answer is 55.26213.

1 solution

Steven Chase
Jan 22, 2018

Apparent, active, and reactive power drawn by motor:

$S = 2000 \\ P = 0.8 \, S = 1600 \\ Q = \sqrt{S^2 - P^2} = 1200$

Required capacitive reactance to offset Q:

$Q = \frac{V^2}{X} \\ X = \frac{V^2}{Q} = \frac{240^2}{1200}$

Capacitance associated with reactance:

$\omega = 2 \pi \, f = 120 \, \pi \\ X = \frac{1}{\omega \, C} \\ C = \frac{1}{\omega \, X} = \frac{1200}{120 \, \pi (240^2)} = 55.26213 \, \mu F$

Here is an alternative solution using complex values, with $j=\sqrt{-1}$ :

Let us represent the motor with an impedance $Z=R+j\omega L$ (a resitor and inductor in series). The nominal power is $S=|U| |I|=|U|^2/|Z|$ , where $|U|$ and $|I|$ are effective values. The real power is $P=|U|^2/|Z| \cos \theta$ , where $\cos \theta= R/|Z|=0.8$ is the power factor. With the numbers in the problem we get $|Z|=\frac{|U|^2}{|S|} = 28.8 \Omega$ and $\omega L=|Z|\sqrt{1-\cos^2\theta}= 17.3\Omega$ .

When the proper capacitor is in parallel with the motor the total impedance is purely ohmic, there is no imaginary part. The total impedance is $(1/Z+j\omega C)^{-1}= (R/|Z|^2-j\omega L/|Z|^2+j\omega C)^{-1}$ . This quantity is real if $-j\omega L/|Z|^2+j\omega C =0$ . Therefore $\omega C =\omega L/|Z|^2=0.0208 \Omega^{-1}$ We get $C= 0.0208/6.28/60= 55.3\mu$ F .

Laszlo Mihaly - 3 years, 4 months ago

I'm thinking it would be fun to post a power factor correction problem for which this type of solution is necessary. In the revised problem, the source would have non-zero impedance, meaning that the addition of the capacitor changes the reactive power consumed by the load (unlike in this simple case). I would also no longer call the load a motor, but simply an RL branch (because motors are commonly considered to be "constant power" devices). Let me know if you would like to post one like that. Otherwise, I will.