Motor Pulley Crate Velocity After Motion

Classical Mechanics Level 3

A motor is mounted to a wall and pulls on a cable as indicated, with $F = 7 t^2 + 400.$ The crate weighs $200 \text{ kg}$ and is at rest at $t_1 = 0.$ Determine the velocity when 8 seconds has elapsed to 2 decimal places.

Take the gravity as $9.81 \text{ m/s}^2$ .

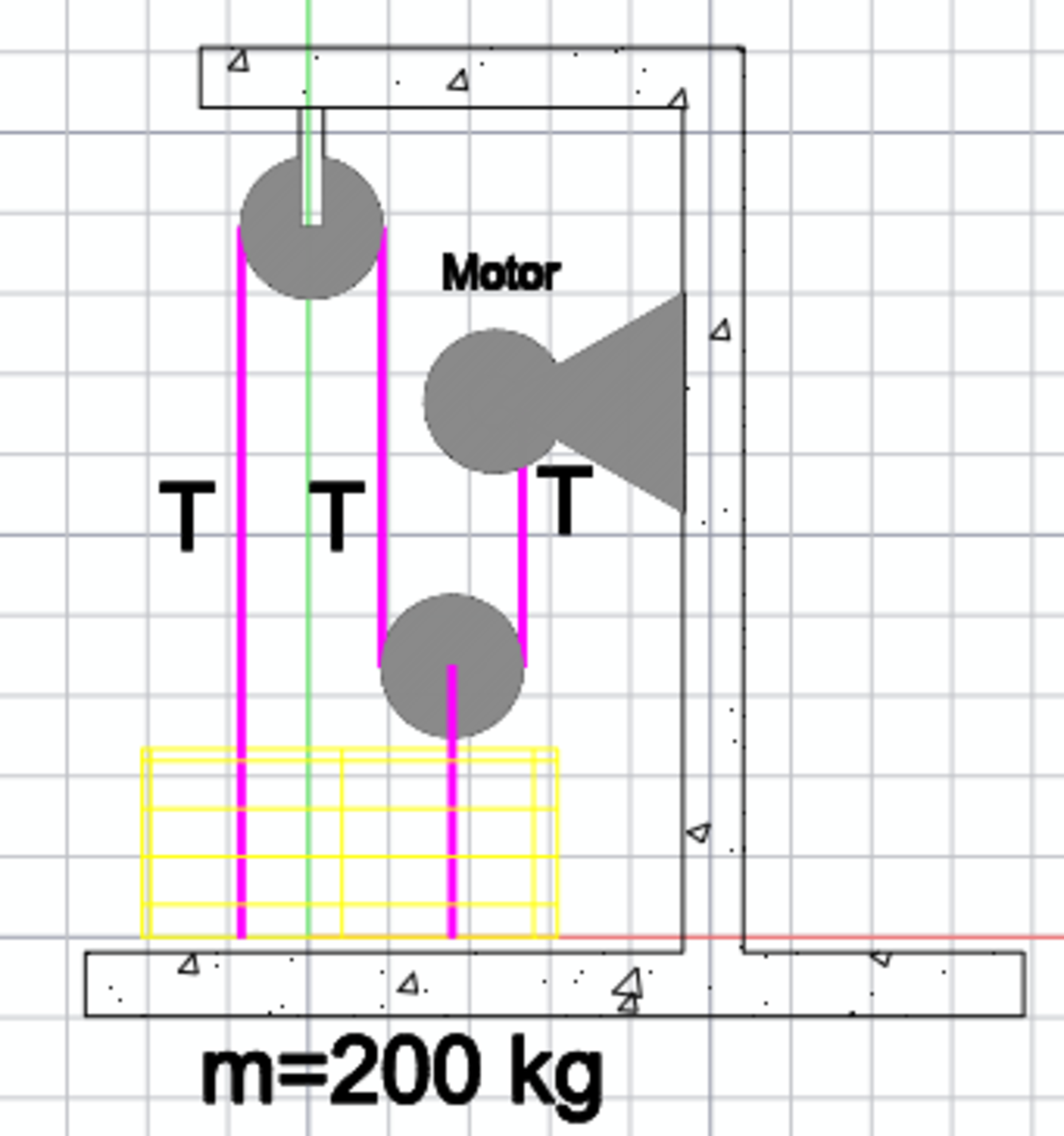
The answer is 2.74.

2 solutions

A Former Brilliant Member
Jan 7, 2021

Steven Chase
Jan 7, 2021

These are always fun. I will post my time domain simulation for the sake of variety. The key here is that the crate only accelerates once the net upward force exceeds the weight. Nice thing about this implementation is that I can use a simple conditional statement to avoid having to pre-calculate the time at which the crate starts to move.

import math

dt = 10.0**(-5.0)  # time step

m = 200.0   # mass
tf = 8.0   # final time
g = 9.81   # grav acc

##############################

t = 0.0       # initialize simulation

x = 0.0     # position
xd = 0.0    # velocity
xdd = 0.0   # acceleration

while t <= tf:           # run until final time

    x = x + xd*dt        # numerical integration

    if xdd > 0.0:           # only apply acc if positive
        xd = xd + xdd*dt 

    T = 7.0*(t**2.0) + 400.0  # cable tension
    F = 3.0*T - m*g           # Force = 3*tension - weight

    xdd = F/m   # acceleration

    t = t + dt

##############################

print dt
print xd

#1e-05
#2.74034212158
#>>>

Thanks for providing your solution, Steven!

A Former Brilliant Member - 5 months ago

Hi Steven, sorry for the mistaken problem the other day. Did you solve it iteratively with a program or use DEQ? I wrote a program and got 4.9 but had to decide how to vary h and took the average of hin and hout and then recalculated a new outflow. Can you post your solution here? Thanks.

A Former Brilliant Member - 3 months, 1 week ago

Hi Joe. No problem, I was actually not sure that I had done it right. I ran a simulation over time, solving differential equations.

import math

dt = 10.0**(-5.0)

H = 10.0
Abase = 16.0

D = 0.5
R = D/2.0
A = math.pi*(R**2.0)

y1 = 1.5
y2 = 5.5

Qin = 5.0
tf = 35.0

g = 9.81
Cd = 0.62

##################################

t = 0.0
y = 0.0           # water level

while t <= tf:

    if y > y1:
        v1 = Cd*math.sqrt(2.0*g*(y - y1))
        Q1 = A*v1
    else:
        Q1 = 0.0

    if y > y2:
        v2 = Cd*math.sqrt(2.0*g*(y - y2))
        Q2 = A*v2
    else:
        Q2 = 0.0

    Qout = Q1 + Q2

    Qnet = Qin - Qout

    # Qnet*dt = Abase*dy

    dy = Qnet*dt/Abase

    y = y + dy

    t = t + dt

####################################

print y
print ""

# y2 = 0.5*g*(t**2.0)

t = math.sqrt(2.0*y2/g)       # time redefined here for a different purpose

xf = v2*t

print xf

#>>> 
#8.44042734559     # water level at t = 35

#4.98664134908     # range of upper stream
#>>>

Steven Chase - 3 months, 1 week ago

@Steven Chase – Thanks a bunch Steven!

A Former Brilliant Member - 3 months, 1 week ago

Well, I solved the integrals and got 8.35m for h and 4.91 for x. Did it in Mathcad but I'm not sure how accurate it is because they use numerical routines to solve when you evaluate integrals. Had to solve for time with different h's. Your incremental time approach seems pretty straight forward, and is much more intuitive. Thanks again for sharing your methodology.

A Former Brilliant Member - 3 months, 1 week ago

Motor Pulley Crate Velocity After Motion

The answer is 2.74.

2 solutions

0 pending reports