Moving Plates Capacitor!
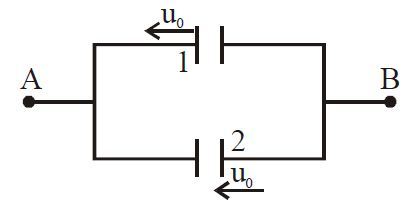 Two identical capacitors having plate separation
1
mm
are connected parallel to each other across points
A
&
B
as shown in figure. Total charge of
4
μ
C
is imparted to the system by connecting a battery across
A
&
B
and battery is removed. Now first plate of first capacitor and second plate of second capacitor starts moving with constant velocity
u
0
=
3
m/s
towards left. Find the magnitude of current (in
mA
) flowing in the loop initially.
Two identical capacitors having plate separation
1
mm
are connected parallel to each other across points
A
&
B
as shown in figure. Total charge of
4
μ
C
is imparted to the system by connecting a battery across
A
&
B
and battery is removed. Now first plate of first capacitor and second plate of second capacitor starts moving with constant velocity
u
0
=
3
m/s
towards left. Find the magnitude of current (in
mA
) flowing in the loop initially.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
correct, did the same way!
( T h a n k y o u f o r y o u r a p p r e c i a t i o n ! )
Log in to reply
Log in to reply
have dropped a year, preparing for JEE Advanced! ⌣ ¨
Log in to reply
@Nishant Rai – Best of luck for advance :) , I 'am too preparing for JEE 2015 Btw , if you don't mind , would you like to tell your mains marks ?
Can be generalised for any time Charge on C2 is QC2/C1+C2 There fore dq/dt = dQ (d1/d1+d2)/dt Whwre d1 and d2 are separation at time t Differentiating using quotient rule we get i at any time t I missed the ans by factor of 2 (calculation mistake)
q = C U so d t d q = U o d t d C we all know that C = ϵ d A that yields i = − ϵ d 2 A U o then i = − ϵ d A d U o then i = − C d U o that yields i = − d Q o because Q o = C U o please note that this is half of the charge in the circuit ,finaly we need the absolute value of the current then ∣ i ∣ = ∣ − 1 0 − 3 3 ∗ 2 μ ∣ ∣ i ∣ = ∣ − 1 0 − 3 6 μ ∣ = 6 m A
Hey bro, gud to see guys r studying in war torn syria
Log in to reply
Syria is a huge country there is War areas and safe areas so Its normal to study in those areas
This came in Allen Online TEst Series, right?
Log in to reply
i think yes. one of my friend showed me this problem.
Initially, each capacitor obtained charge of 2 μ C respectively with connected plates of equal voltage.
C V = Q
ϵ 0 A ( 0 . 0 0 1 V 1 + 0 . 0 0 1 V 2 ) = 4 × 1 0 − 6
As V 1 = V 2 = V ,
ϵ 0 A 0 . 0 0 1 2 V = 4 × 1 0 − 6
ϵ 0 A V = 2 × 1 0 − 9 = Constant {A fact for unchanged total charges.}
It follows that
ϵ 0 A x 1 V 1 = Q 1 and ϵ 0 A x 2 V 2 = Q 2
⟹ Q 1 x 1 = Q 2 x 2 = ϵ 0 A V = 2 × 1 0 − 9
⟹ Q x = 2 × 1 0 − 9
⟹ Q d t d x + d t d Q x = 0
I = d t d Q = − x Q d t d x = - 1 × 1 0 − 3 2 × 1 0 − 6 × 3 = − 6 × 1 0 − 3
| I | = 6 m A
On negative side, electrons flow from separating plates onto closing plates to add up negative strength; on positive side, electrons flow from closing plates onto separating plates to deduct away positive strength. The current is therefore one directional. Voltage onto both capacitors are equal through out the process and total charges are constant. It is d t d V = 0 at least at t = 0 that makes a simpler calculation allowed.
Answer: 6
Nice Problem , however pretty simple as well ! I see you are contunisly posting beautiful physics problems , I appreciate you for this . Keep Posting more !
Let at t = t , x = v t distance is moved by both plates , hence sepration b/w plates is increasing , and other has decresing , But potential diff is same on both capacitor , So charge will flow from higher capcitance plate( 2 - plate ) to lower capicatance plate (1-plate) .
So we just equate pot. diff of both plates :
V 1 = V 2 q 1 / C 1 = \sfrac q 2 C 2 ( 2 Q o − q ) ( d + x ) = ( 2 Q o + q ) ( d − x ) . . . ( : Q o = 1 μ C ) 2 Q o + q 2 Q o − q = d + x d − x A p p l y c o m p . a n d d i v d e n d o : 2 Q o − q = d − x q = ( d 2 Q o ) x I = d t d q = ( d 2 Q o u o ) = 6 m A A n s .