Moving Wedge
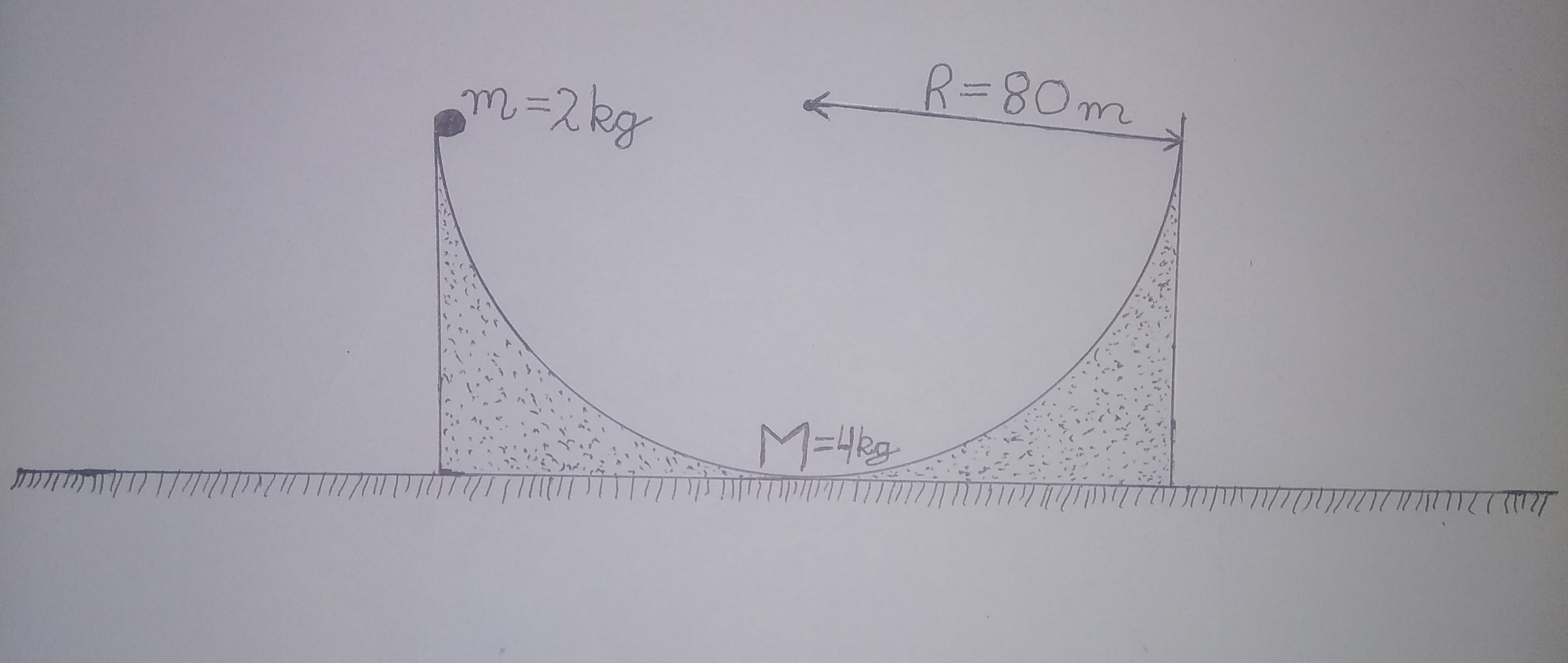
A wedge of mass M = 4 kg and a particle of mass m = 2 kg are arranged as shown in above figure. The wedge is semicircular, has radius R = 8 0 m and is free to move . Find time period = T of above system in seconds .
Enter answer as T .
Details and Assumptions
-
All surfaces are smooth
-
Take acceleration due to gravity g = 1 0 m / s 2 .
-
Wedge is free to move
Inspiration Aniket Sanghi
All of my problems are original
The answer is 19.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Aryan Sanghi
i also solved it same way.
For your extreme hardwork for typing this solution i have upvoted .
@Aryan Sanghi i was just thinking that, can you try to make a problem in which we can vary μ in wedge.
Log in to reply
I am not familiar with friction on curved surfaces, so maybe I wont be able to. But I'll try to make. :)
Log in to reply
Friction on curved surfaces will be the same. However, normal force m g cos ( θ ) will differ. This is why you should use a numerical solution if you are willing to add friction, because normal force will change a lot.
How about this one?
No, normal reaction will do work. Here, body isn't moving perpendicular to normal reaction. It makes a non 90° angle with body
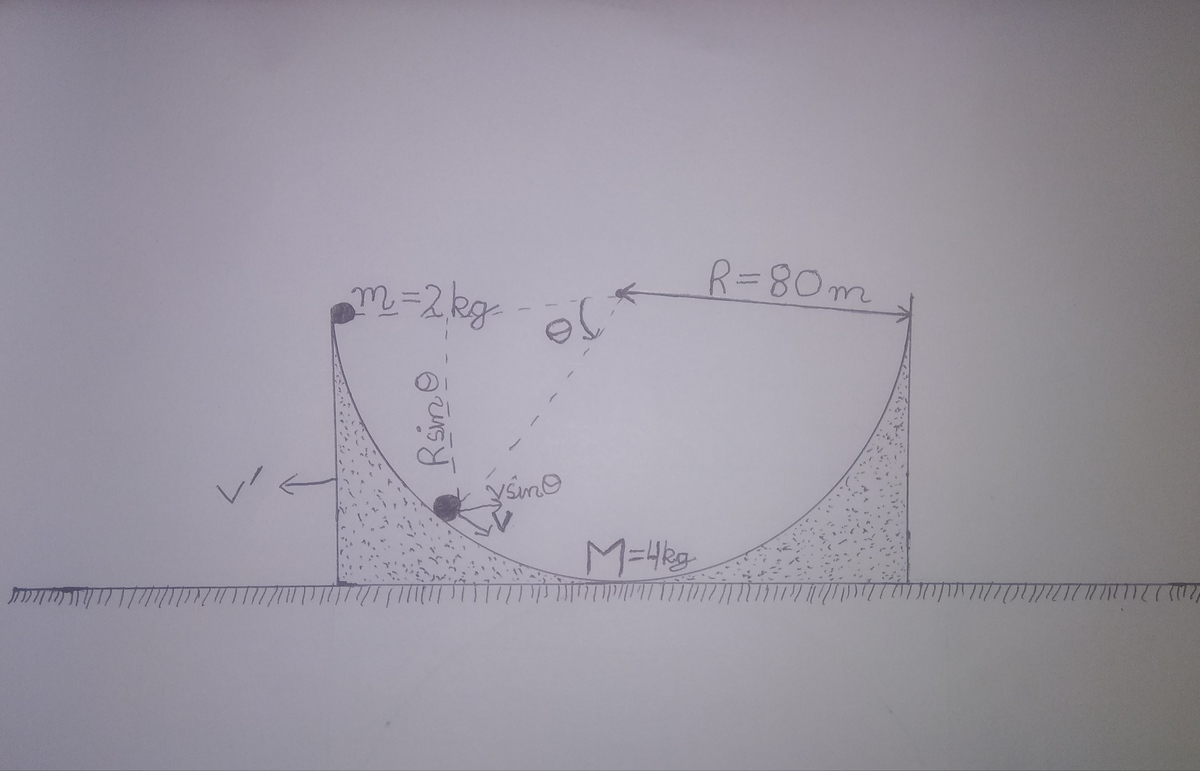
Let the coordinates of the particle be ( x , y ) , and let the center axis of the wedge be at position x 0 . The position and velocity of the particle are:
x = x 0 + R cos θ y = R + R sin θ x ˙ = x ˙ 0 − R sin θ θ ˙ y ˙ = R cos θ θ ˙
Combined kinetic energy of the particle and the wedge:
T = 2 1 m ( x ˙ 2 + y ˙ 2 ) + 2 1 M x ˙ 0 2 = 2 1 m ( x ˙ 0 2 − 2 x ˙ 0 θ ˙ R sin θ + R 2 θ ˙ 2 ) + 2 1 M x ˙ 0 2
Gravitational potential energy of the particle:
V = m g y = m g ( R + R sin θ )
Lagrangian:
L = T − V = 2 1 m ( x ˙ 0 2 − 2 x ˙ 0 θ ˙ R sin θ + R 2 θ ˙ 2 ) + 2 1 M x ˙ 0 2 − m g ( R + R sin θ )
Equations of Motion:
d t d ∂ x ˙ 0 ∂ L = ∂ x 0 ∂ L d t d ∂ θ ˙ ∂ L = ∂ θ ∂ L
Evaluating results in the following system of equations to be solved for the second derivatives:
[ m + M − m R sin θ − m R sin θ m R 2 ] [ x ¨ 0 θ ¨ ] = [ m R cos θ θ ˙ 2 − m g R cos θ ]
Initialize a numerical solution as follows:
x 0 ( 0 ) = 0 θ ( 0 ) = 0 x ˙ 0 ( 0 ) = 0 θ ˙ ( 0 ) = 0
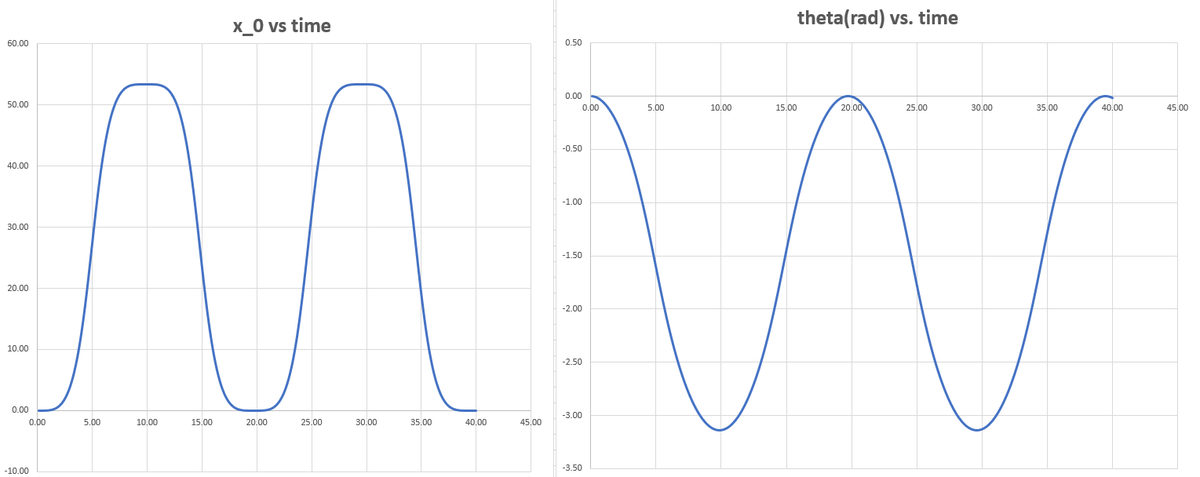
On each time step, solve the linear system for the double-dot terms, and numerically integrate. Plots of x 0 and θ are given below. The period of motion is about 1 9 . 7 3 . Simulation code is also attached.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
|
Excellent solution sir. Thanku for sharing it with us. :)
Log in to reply
Thanks. Nice job solving it with conservation principles too. It's tempting to ask why the vertical momentum doesn't have to be conserved.
Log in to reply
It's because there is gravity in vertical direction, so momentum isn't conserved, isn't it?
Log in to reply
@Aryan Sanghi – I suppose in the real case of a ball falling toward the Earth, the Earth actually moves upwards very very slightly to conserve momentum (and because of equal and opposite forces). But the effect is so small that it can't even be measured.
Log in to reply
@Steven Chase
–
@Steven Chase
instead of saying can't even be measured you should say, right now we don't have such advanced equipments to measure that effect.
But don't worry ,I will definitely try to make that equipment.
I initially attempted solving it this way. With a time step of 1 0 − 4 s , I obtained a result of T ≈ 1 9 . 1 2 5 7 . I noticed that the solution took a significantly long time while using a time step of 1 0 − 5 s . I was wondering if you observed the same?
Log in to reply
There was a bug in my code. I have resolved it and it is now okay
Log in to reply
It takes some seconds to run, but I don't consider that to be a long time
Log in to reply
@Steven Chase – It was taking me more than a minute. The condition based on which I ran my loop was flawed.
Log in to reply
@Karan Chatrath – Yeah, my strategy was to make a plot to get an idea of the behavior. Then I looked for a local maximum corresponding to one elapsed period, and stored the associated time.
Log in to reply
@Steven Chase – Yes, I modified my code based on your solution. Mine relied on numerical tolerances which were not giving a good estimate.
Log in to reply
@Karan Chatrath – Numerical techniques are a bit of a black art
Log in to reply
@Steven Chase – @Steven Chase what does Black Art mean?
Log in to reply
@Talulah Riley – It means that there is no pre-defined recipe that will guarantee success. One has to rely on judgement and experience.
Log in to reply
@Steven Chase
–
@Steven Chase
Oh yeah.
Searching on internet, it shows me skull. Lol.
Log in to reply
@Talulah Riley – @Lil Doug XD
He means it's like a dark art.
I would just like to ask: Is this a coupled system of equations? If so, would you have to use Linear Algebra to solve a coupled system?
Log in to reply
Using linear algebra is not necessary, but is quite convenient. It saves one the effort of manually solving for the acceleration expressions.