Multiple of 3's digits and 0's digits

Relevant wiki: Pigeonhole Principle - Problem Solving

Take the infinite set of the numbers ${3, 33, 333, 3333, ...}$ there exist two numbers have the same remainder when divided by 2018. Take those numbers and the difference would be a number of the form $333...33300..00$ which is divisible by 2018.

Relevant wiki: Fermat's Little Theorem

Since $1009$ is prime, by Fermat's little theorem $10^{1008} - 1$ is divisible by $1009$ . Written out, this number would consist of $1008$ $9$ s, which means it is divisible by $3$ , and dividing this number by $3$ would give a number that consists of $1008$ $3$ s that is still divisible by $1009$ .

Now multiplying this number ( $\frac{10^{1008} - 1}{3}$ ) by $10$ would give a number that consists of $1008$ $3$ s followed by one $0$ .

This new number ( $\frac{10^{1008} - 1}{3} \cdot 10$ ) consists only of the digits $3$ and $0$ , and is divisible by $2$ and $1009$ , which means it is also divisible by $2018$ .

Relevant wiki: Modular Arithmetic - Problem Solving - Intermediate

Since $1009$ is prime, $10^{1008} \equiv 1 \pmod{1009}$ . In fact we can show that $10^{252} \equiv 1 \pmod{1009}$ , and that $10^{126} \equiv -1 \pmod{1009}$ . Thus $10^{126} + 1 \equiv 0 \pmod{1009}$ , so that $10^{127} + 10 \equiv 0 \pmod{2018}$ , and hence $3(10^{127} + 10) \equiv 0 \pmod{2018}$ .

$\begin{array}{cccc} 10^{2} \equiv &100&&mod(1009)\\ 10^{9}\equiv &280&&mod(1009)\\ 10^{14}\equiv&250&&mod(1009)\\ 10^{23}\equiv&379&&mod(1009) \end{array}$ \

100 + 280 + 250 + 379 = 1009 so\ $10^{23}+10^{14}+10^{9}+10^{2}\equiv 0\quad mod(1009)$ \ $10^{23}+10^{14}+10^{9}+10^{2}$ even number so $10^{23}+10^{14}+10^{9}+10^{2}$ divisible by 2018, likewise $3\times(10^{23}+10^{14}+10^{9}+10^{2})$ divisible by 2018. So, for example, 300000000300003000000300 divisible by 2018.

we know a number is divisible by three whenever the sum of its digits is divisible by three. because on the right side there is a sequence of 3 and 0, so the left side should be multiple of 3, which means: $2018*3*Z=30033....330..303$ . so if we simplify both sides of the equation it turns out we are looking for some Z that satisfy equation $2018Z=1 .10011..110..101$ , the right side means a sequence of 0 and 1. So the easiest way to obtain this sequence is to look at the binary representation of 2018 and multiply each bit significant $i$ to $10^i$ . so after got Z, then K can obtain from $3*Z$ .

Just trying and adjusting by hand... and with the little help of a spreadsheet doing the multiplication algorithm:

$150\,298\,975\,720\,185\times 2018=303\,303\,333\,003\,333\,330$

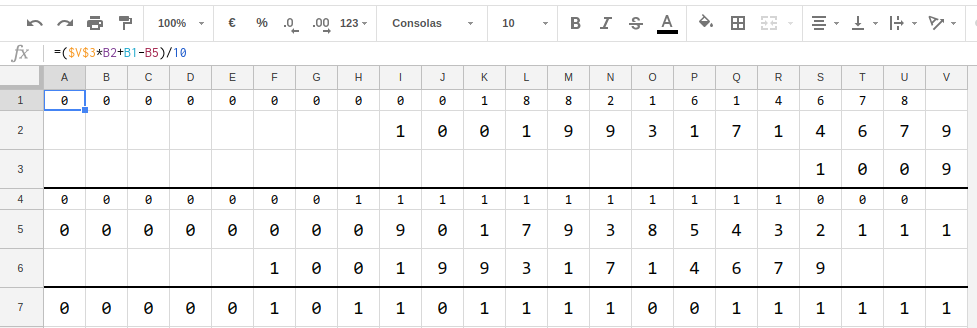As you see in the image, working with 1009 you just need a multiple of it consisting of 1's and 0's, and when you have it, multiply it by 15.

2018 multiplied by 3000 for example

Consider the first 2019 numbers 3, 33, 333, ... , 333...33 (2019 threes in total). By pigeonhole principle, there will be two of them that are congruent mod 2018. These two numbers’ difference is apparently divisible by 2018 and only consists of the figures 0 and 3, i.e. it has the required properties.