Multiply To Win
Alice and Betty are playing a game. Each turn, they choose a positive integer which hasn't been previously chosen. A player wins if, among the numbers that the player has chosen, there are three different numbers a , b , c such that a b = c . (In particular, no player can win by having only chosen one or two numbers.)
Assuming perfect play, if Alice goes first, who has a winning strategy?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
it is interesting if you try to extend the problem to 3 people
Log in to reply
The problem with games of more than 2 players is that there are kingmaker situations. Suppose we're A. Suppose A or B will win on their next turn; C has no hope. But it's C's turn right now, and they can block either A or B (not both). Which one are they going to block? What if it's B that has no hope instead? Do B and C cooperate to try to make A fail and not caring which one of them wins? This is why most combinatorial games like this involve only 2 players (or 2 sides, or whatever).
So let's throw a mix. Two teams of two, A1 and A2 versus B1 and B2. The turn order is A1, B1, A2, B2. All numbers that make the multiplication must be chosen by a single player (otherwise it's the same thing), but whoever gets the multiplication brings the win to their team (so if A2 can help A1 to win, they do so, because that means A2 wins as well as a team). Who wins; what's the first move?
Log in to reply
i don't think kingmaker situations will arise if you follow the rules set by Calvin ,As for A and B both with winning moves on next turn, C can block A and A can block B.
but you're right its too complicated to check all the cases, your idea of teams sound cool. will surely think about a strategy for teams :)
Log in to reply
@Anirudh Sreekumar – That's precisely the problem; you must stipulate the rules set by Calvin into the problem as well, because without that you can imagine all other sorts of possibilities of what the priorities of each person are.
(Also, ah, my mistake. B can win in two different ways, so if C blocks A, A cannot block B. Thus either C blocks A and lets B to win, or C doesn't block A and hence A wins. That's the kingmaker situation. If there's only one way B can win, then C wins by blocking A, forcing A to block B and thus continuing the game and allowing C another chance.)
Can you post that problem?
Log in to reply
This is under the assumption that each player plays to prevent the next person from winning
the combination i have come up with is
what are your thoughts??
Log in to reply
@Anirudh Sreekumar – I think it's fair to assume that the priority of moves are
- Self to win in this 1st move
- Prevent next player to win in their 1st move
- Prevent next next player in win in their 1st move
- Self to win in 2nd move
- Prevent next player to win in their 2nd move
- Prevent next next player to win in their 2nd move
- ETC
- (Maybe) Do anything
I do not think it's fair to assume that Bob would play a 2 . That to me doesn't make sense, since it doesn't help Bob to eventally win (there are likely better options to play), and doesn't really prevent Alice from winning,
I think that Alice also will end up winning, but it's not immediately obvious how / why. IE She will have to play a value that opens up 3 winning possibilities, so as not to get blocked by Bob and Charlie.
Though, it's also possible that if Alice plays to block Bob, then Charlie could win. So, I'm not too certain who the real winner would be.
This variant is turning out to be really interseting :)
Really great solution.
Oh nice! @Chung Kevin This shows that we do not need " n = a × b = c × d (all distinct)" for Alice to win on the third move. In fact, any number other than 1 works!
Why could Alice win if she followed Bob strategy and is the second player? Shouldn't Bob win first?
Log in to reply
If the second player has a winning strategy, that must also involve blocking the first player when they are near winning; that's part of the strategy. If they don't block it, then it's not a "winning" strategy.
If Alice chooses 36, she is guaranteed a win. This is how:-
If Betty does not choose 18, alice chooses 18 creating a fork threatening 2 and 36*18.
If Betty chooses 18, Alice chooses 12 creating a fork threatening 3 and 12*36.
This strategy finishes the game before Betty can choose her 3rd integer meaning that it is impossible for Betty to win against this strategy.
Another similar strategy is possible beginning with 16 which is probably the smallest number for win in 3 but we need to tackle 3 cases.
Alice has wants a number with a lot of factors to win. Once you realize that, the rest is straightforward.
In fact, as long as n = a × b = c × d (all distinct), then Alice can win on her third move.
The smallest first move which guarantees Alice the win is 2.
Alice wins by literally playing any positive integer a except 1.
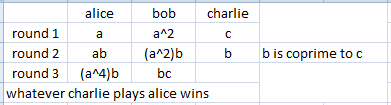
Whatever Bob chooses, Alice can find a b such that none of b , a b , a 2 b were chosen by Bob. (For example, just pick b to be larger than Bob's move.) Alice chooses a b . Next turn, Alice chooses either b (winning by a × b = a b ) or a 2 b (winning by a × a b = a 2 b ); at least one of them is not blocked because neither were blocked before Alice's turn, and Bob can only block one. Since by this time Bob has chosen only two integers, Bob couldn't have won, so Alice wins.
Extra: We can prove that Bob cannot win by strategy-stealing argument. Suppose Bob can win. Then Alice plays any number and follows Bob's strategy. An extra number is never detrimental for Alice; if Alice ever needs to select a number that she already played before, just play some other random number. This way, Alice is effectively playing second, and thus should win because we assumed there's a winning strategy for Bob (second player), contradiction. Thus Bob cannot win. This doesn't prove that Alice will win, though, since the game can last forever (and thus there's no winner).