Multitalented Multi - Conductors!
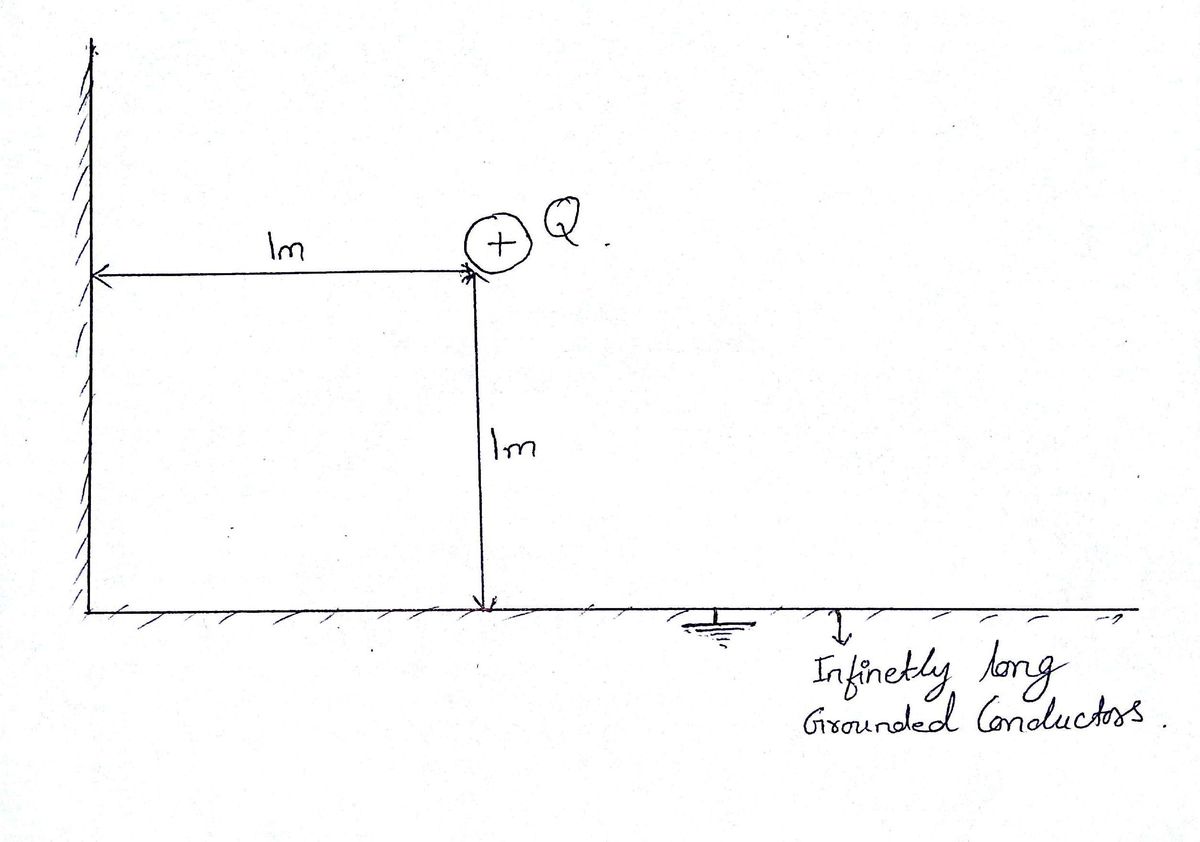
A Charge Q ( of mass m ) is placed symmetrically as shown between two infinitely long grounded conducting sheets . Now the charge is left free when it is at a distance of 1m from each of the sheets .
Find the time taken by it to collide with the conductors.
If your answer can be represented as
e Q 2 a b π 3 m ϵ ° ( c d + 1 )
Where a and e are co-prime integers and b and d are square free integer and c is also an integer.
Enter Your Answer as a × b × c × d × e
Original
This is a part of my set Aniket's Electrostats Challenges
The answer is 224.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Congrats... Nice sol.....+1:)
Log in to reply
I have recently started learning EM stuffs and they are pretty awesome+intresting!
Can you refer some resources from where you studied 'em?
Log in to reply
Griffith's,Edward Purcell and David.J.Morin,Feynman's etc.I first completed HCV,and Irodov EM and then studied these for Olympiads.
Yes I particularly like the Maths involved here...Curl,Divergence,Laplace eq,Poisson's eq.,Greens Theorem etc are really some very interesting things in EM.
Could u please elaborate .I am not quite able to get it
Log in to reply
Its better of you refer to the image charge theory from say(Feynman's Lectures in Physics,Vol-2 or Edward M Purcell,David J.Morin's book,or any other book coz this is quite a standard prob which you can easily solve once you read it.
Log in to reply
ok thanks :)
Log in to reply
@Zerocool 141 – i asked for a proper solution as i have read image theory but am confused and am not able to approach this problem
Does the fact that the charge and its mirror image are moving have no effect whatsoever on the credibility of the method of mirror images? The moving charge would also produce a magnetic field, which will definitely affect the behaviour of the image charge etc. Could someone please elaborate on why this method is still applicable, or maybe explain how to make the necessary corrections? Thanks in advance!
Log in to reply
We don't have the physical existence of an image charge.Treat the system as 2 conductor s and the given charge.So even if you were to take the magnetic field of the point charge it won't effect the statics of the problem.And secondly considering the speeds are negligible compared to speed of light the ratio F ( m a g ) / F ( e l e c t r i c ) = ( v / c ) 2 is quite negligible. So anyways Magnetic field doesn't affect the motion and neither the statics of the problem.
I used the method of image charges ( may be the standard approach ).
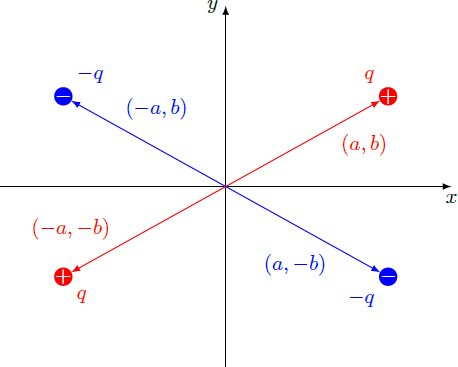
In the picture above the red dots represent positive charge and the blue dots represent the negative charge.
Now from the Coulomb's law we have(as shown in the above picture):
F 1 = 4 π ϵ 0 ( 2 a ) 2 − q 2 a y
F 2 = 4 π ϵ 0 ( 2 b ) 2 − q 2 a x
F 2 = 4 π ϵ 0 ( ( 2 a ) 2 + ( 2 b ) 2 ) 2 3 − q 2 ( a x 2 b + a y 2 a )
So now we have F = F 1 + F 2 + F 3
⇒ F = 1 6 π ϵ 0 q 2 [ a x ( ( a 2 + b 2 ) 2 3 b − b 2 1 ) + a y ( ( a 2 + b 2 ) 2 3 a − a 2 1 ) ]
⇒ ∣ F ∣ = 1 6 π ϵ 0 q 2 [ ( ( a 2 + b 2 ) 2 3 b − b 2 1 ) ] 2 + [ ( ( a 2 + b 2 ) 2 3 a − a 2 1 ) ] 2
⇒ − m a = 1 6 π ϵ 0 q 2 [ ( ( a 2 + b 2 ) 2 3 b − b 2 1 ) ] 2 + [ ( ( a 2 + b 2 ) 2 3 a − a 2 1 ) ] 2
where a is the acceleration and is given by:
⇒ a = − 1 6 π ϵ 0 ⋅ m q 2 [ ( ( a 2 + b 2 ) 2 3 b − b 2 1 ) ] 2 + [ ( ( a 2 + b 2 ) 2 3 a − a 2 1 ) ] 2
Also observe that the positive charge is symmetrically distant from both the infinite conductors so its path will be a straight line joining the point at which both the conductors meet. Hence we can take a=b=x(as given in the image). Putting this in the above equation we get
⇒ a = − 1 6 π ϵ 0 ⋅ m q 2 x 2 ( 2 2 − 1 )
Now let k = 1 6 π ϵ 0 ⋅ m q 2 ( 2 2 − 1 )
We know a = v ⋅ d x d v .
⇒ v ⋅ d x d v = − x 2 k
⇒ v ⋅ d v = − x 2 k ⋅ d x
⇒ ∫ v ⋅ d v = − ∫ x 2 k ⋅ d x
Now integrating and applying the initial condition that at x = 1 , v = 0
⇒ 2 v 2 = k ( x 1 − 1 )
⇒ v = − 2 k ( x 1 − 1 )
⇒ d t d x = − 2 k ( x 1 − 1 )
⇒ t f = ∫ 1 0 2 k ( x 1 − 1 ) − 1 ⋅ d x
⇒ t f = ∫ 0 1 2 k ( x 1 − 1 ) 1 ⋅ d x
Computing the integral we have:
⇒ t f = 2 2 3 ⋅ k π
⇒ t f = 7 q 2 4 2 π 3 m ϵ ° ( 2 2 + 1 )
Therefore a = 4 , b = c = d = 2 , e = 7 .
⇒ a × b × c × d × e = 2 2 4
My 1st LEVEL 5 EM 400 points problem.
Congrats! :)
Log in to reply
Thank you. @Aniket Sanghi , did you give nsep. I don't think of being selected in class 10 but want to give being prepared. Can you suggest some topics that I can skip as I will give in November.
Method of images kills this problem.
Just we want a configuration where net potential on the conductors is zero.Clearly a configuration of charges placed placed on the vertices of square ABCD where adjacent vertices charges have equal magnitude and opposite nature.The equipotential lines here pass through the perpendicular bisectors of the sides of squares.Now just do the basic computations and our answer comes.
a=4
b=c=d=2
e=7
abcde = 224
My first lvl5 EM problem i solved on brilliant :P