Ninja Turtle!

Without considering the eyes of the ninja turtle (two circles), the area of the blue region is composed of two circular sectors with central angle of $60^\circ$ and two isosceles triangles (it has two equal sides of length $2$ and an included angle of $120^\circ$ ). So the area of the visible blue region is equal to the area of the blue region minus the area of the two circles. We have

$A=2\left(\dfrac{30}{360}\right)(\pi)(2^2)+2\left(\dfrac{1}{2}\right)(2)(2)(\sin 120)-\dfrac{\pi}{4}(1^2)=\dfrac{4}{3}\pi+4\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\pi}{2}=\dfrac{4}{3}\pi + 2\sqrt{3}-\dfrac{\pi}{2}=\boxed{\dfrac{5}{6}\pi +2\sqrt{3}}$

Notes:

1. $\text{area of a circular sector =}\dfrac{\theta}{360}\pi r^2$ where $\theta$ is the central angle and $r$ is the radius

2. $\text{area of a triangle =} \dfrac{1}{2}ab \sin C$ where $a$ and $b$ are two adjacent sides and $C$ is the included angle

3. $\text{area of a circle given diameter}=\dfrac{\pi}{4} d^2$ where $d$ is the diameter.

4. $\sin 120 = \dfrac{\sqrt{3}}{2}$

We can divide the blue band into two congruent sectors and two congruent triangles by drawing two diameters as shown above.

Area of sector = $\frac{60}{360} \times π(2)^{2}$ = $\frac{2}{3}π$

There are two of these so the area of both the sectors combined is $\frac{4}{3}π$

Area of triangle = $\frac{1}{2} \times 2 \times 2 \times \sin 120°$ = $\sqrt{3}$

There are two of these so the area of both the triangles combined is $2\sqrt{3}$

So the area of the blue band is $\frac{4}{3}π + 2\sqrt{3}$

Now we have to subtract the areas of the two smaller circles.

Area of smaller circle = $π (\frac{1}{2})^{2}$ = $\frac{1}{4}π$

There are two of these so the area of both the smaller circles combined is $\frac{1}{2}π$

So the area of the visible blue band is $\frac{4}{3}π + 2\sqrt{3} - \frac{1}{2}π$ = $\boxed {\frac{5}{6}π + 2\sqrt{3}}$

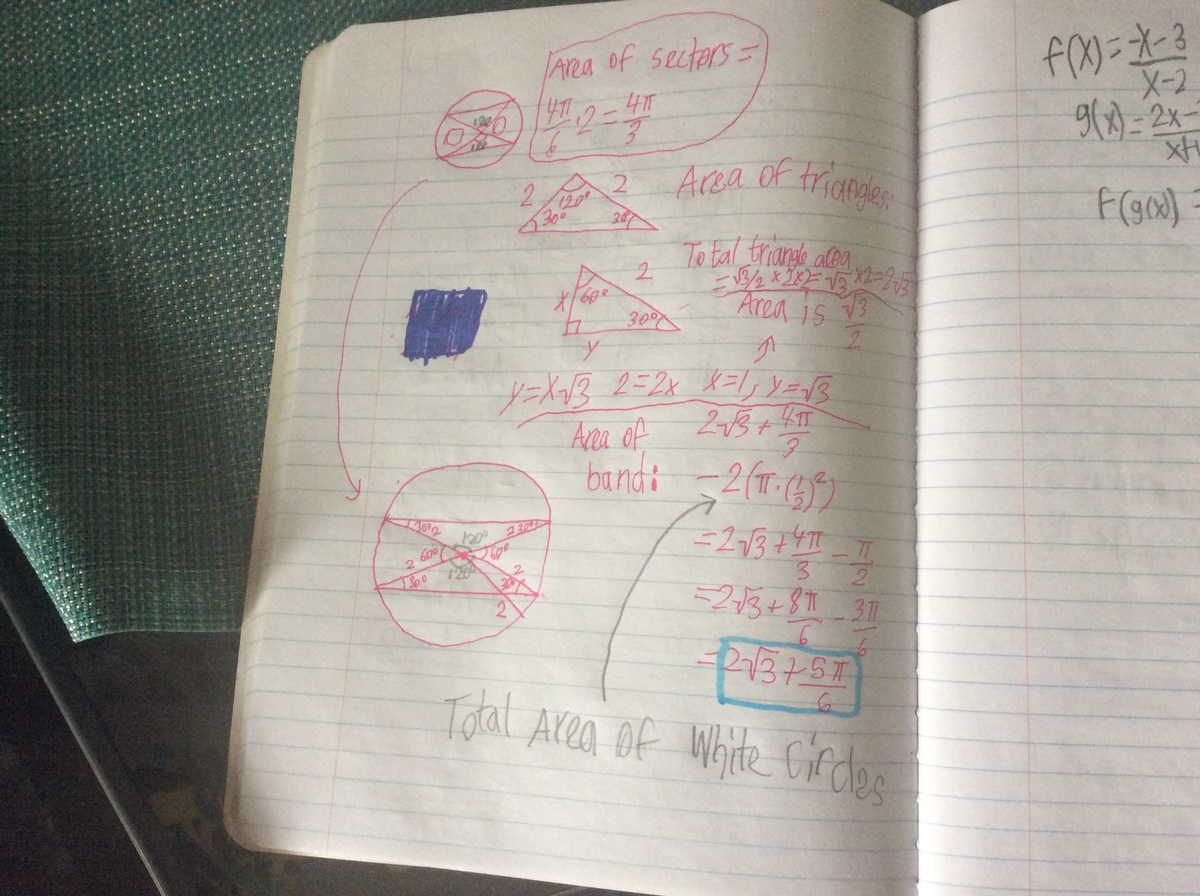
I solved without using trigonometry.

Blue area = Large circle - 2 green segments - 2 white circles

= 4π - 2(4π/3 - √3) -π/2

= 5π/6 + 2√3

Area of 2 sectors = (πr^2)/3 since 60 degrees sector. Area of small circles (eyes) = 2 x π x (1/2)^2 = 1/2π Area of 2 triangles = 2*sqrt(3). Use trigonometry. Visible Blue Area = 4/3π-1/2π +2/3 = 5/6π + 2/3