Acceleration of a cotton reel
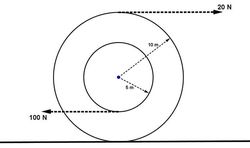Two forces of
1
0
0
N
and
2
0
N
act on a cotton reel of inner radius
5
m
and outer radius
1
0
m
as shown in the figure above. The reel is performing pure rolling motion. The surface produces sufficient necessary friction for pure rolling of the reel. Find the linear acceleration of the reel (in
m/s
2
).
Details and Assumptions
-
The mass of the cotton reel is 1 0 kg .
-
The moment of inertia of the reel about central axis is 1 0 0 0 kg m 2 .
The problem is original.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sir if u take right positive then disc obviously rotates in clockwise direction. Then how u can take this positive in counterclockwise. Please state where am I wrong.
Log in to reply
Correction made. Thank!
Log in to reply
OK . actually I got myself confused but ur solution helped to understand.thanks.
The sense of rotation of the reel would be clockwise. Let
f
be the frictional force,
a
be the linear acceleration and
α
be the angular acceleration of the reel.
Equation of translational equilibrium :
2
0
+
f
−
1
0
0
=
1
0
a
.
Since the body is in pure rolling motion,
a
=
1
0
α
f
−
8
0
=
1
0
0
α
Equation of rotational equilibrium :
2
0
0
−
1
0
f
+
5
0
0
=
1
0
0
0
α
.
f
=
7
5
N
.
Substituting this value in the first equstion, we get acceleration as.
a
=
−
0
.
5
m
/
s
2
.
which implies the actual sense of rotation would be counterclockwise.
rotation is counter clockwise and not clockwise.
Log in to reply
yes he has written wrong and that is what i was pointing to.
Yeah it was a typo, thank you for mentioning.
One can use the fixed point approach too. I mean by just shifting the center of rotation from cm to touching point.
Log in to reply
I always prefer taking moment about the point where the inertia is given.
Log in to reply
Fixed point approach make this problem much easier.
Log in to reply
@Surya Prakash – I don't think this problem deserves a level 5. I mean, it's good, but maybe a level 4?
Log in to reply
@A Former Brilliant Member – Yes you are right.
Log in to reply
@Surya Prakash – The main part is framing the translational, rotational equations, and pure rolling condition. And then it's just solving them linearly. :D.
But, still, nice job with the problem
@Kartik Sharma Yes you are right, in fact i used that also.:D
the sense of rotation will be anticlockwise ....and it will move to its left.
I think there is something wrong .Rohit If the sense of rotation is clockwise(in ur solution) that means reel would go to right. Now for equation 1 u have assumed right as positive direction.But putting f = 7 5 N in equation 1 we get a = − 0 . 5 so it will go to left.
Also for that τ = I α u assumed clockwise as positive but putting f = 7 5 N α comes out to be negative so anticlockwise.
I think right equations should be :
Assuming left to be positive -
1 0 0 − 2 0 − f = 1 0 a = 1 0 0 α
8 0 − f = 1 0 0 α
5 0 0 + 2 0 0 − 1 0 f = 1 0 0 0 α
7 0 − f = 1 0 0 α
which gives no solution!!!. What do u say?
Edit:I forgot a minus sign.Sorry
Log in to reply
your first equation should be 20-100+f=10a
and it will rotate anticlockwise. and it will move to its left.
Log in to reply
my first equation is correct bcoz i assumed left to be positive and also i was pointing out mistake in rohit's solution that it will rotate clockwise.Also rohit's statement and equation do not satisfy.
Log in to reply
@Sandeep Sharma – then your 2nd equation is incorrect. if u have taken left to be positive then 2nd eqn would be 10f-200-500=1000(alpha).
The rotation is anticlockwise. It can't be clockwise.
Log in to reply
yes i m saying same but see rohit's solution he has said the rotation would be clockwise. @Surya Prakash
why are my equations incorrect. The paragraph is for rohit's solution and after that the equations below are mine. @Surya Prakash . edit:I forgot the negative sign.sorry but rohit's solution is incorrect.
You could assume any sense of rotation as per your choice. If your assumption was wrong, your answer would simply come out to be negative.
Basic equations: F f + F 1 − F 2 = m a , R F f − R F 1 − r F 2 = I α . (I choose to the right = positive, clockwise = positive.)
Divide last equation by R , subtract from first, and use that for rolling, α = − a / R : 2 F 1 − R R − r F 2 = m a − R I α = ( m + R 2 I ) a ; substitute known values, a = m + I / R 2 2 F 1 − ( R − r ) / R F 2 = 1 0 + 1 0 0 0 / 1 0 2 2 ⋅ 2 0 − 0 . 5 ⋅ 1 0 0 = 2 0 − 1 0 = − 0 . 5 m/s 2 .