My ultimate Sangaku part 1
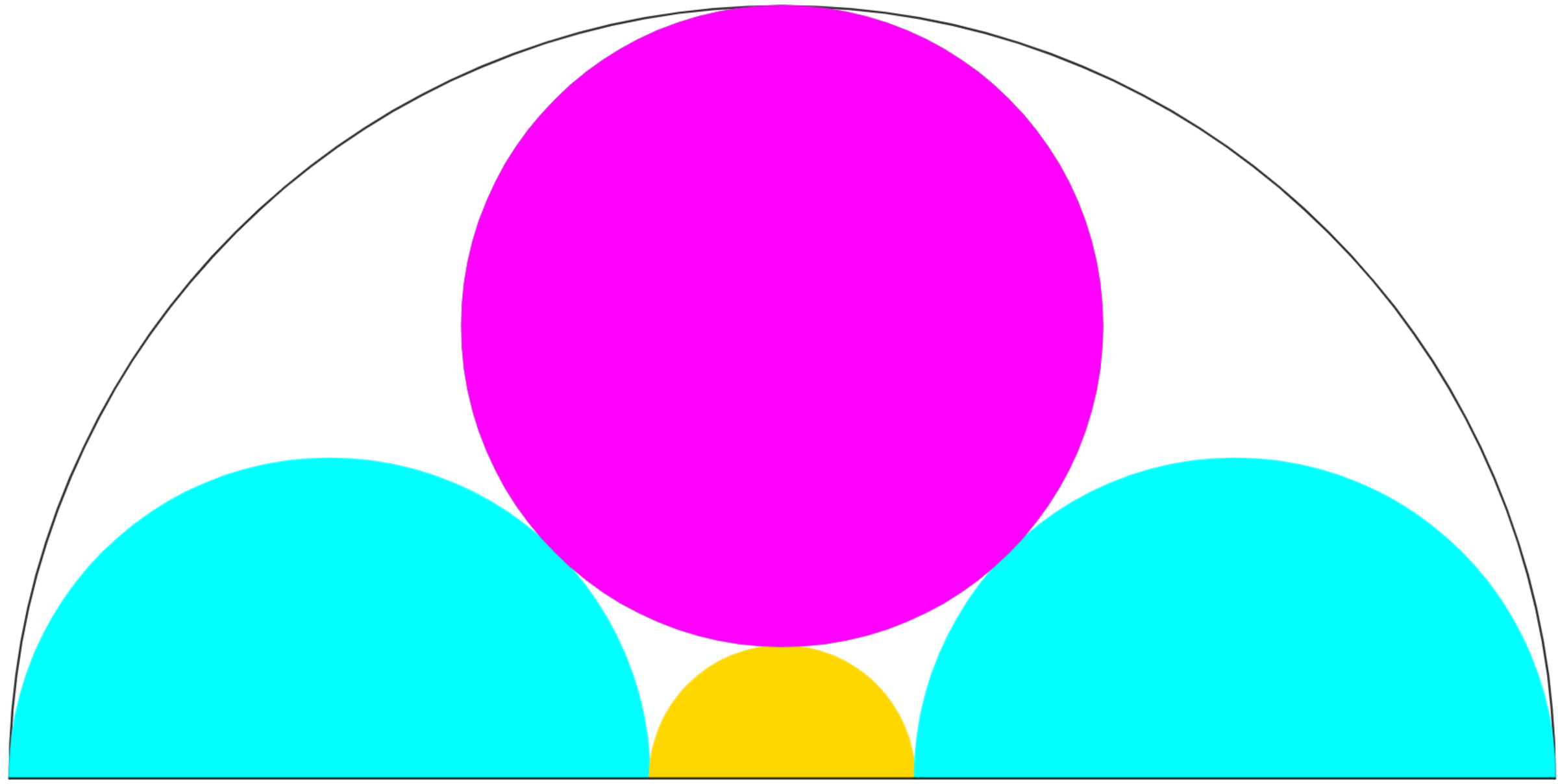
- The diagram shows a black semi-circle with radius 1 .
- The blue semi-circles are equal.
- The blue and yellow semi-circles and the purple circle are tangent to each other. The pink circle and black semi-circle are tangent to each other.
Question : The white area inside the balck semi-circle can be expressed as π ( a b − c ) where a , b and c are positive integers, b is a square free. Evaluate b a ⋅ c + ⌈ π ⌉
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Valentin Duringer , you have to mention b is square-free because 1 0 2 = 5 8 = 2 5 0 = 4 0 0 .
Log in to reply
sure sorry
I would be happy if you could solve my problems that no one wants to solve =)
I got the area π ( 5 2 √ 2 − 7 3 ) I don't know where it went wrong
Log in to reply
That's odd...
Log in to reply
I forgot to reduce the radius from √ 2 + 1 1 to √ 2 − 1 .
I think that matters
Log in to reply
@A Former Brilliant Member – No, this has no effect because 2 + 1 1 = 2 − 1 .
Log in to reply
@Chew-Seong Cheong – Yeah, maybe it's wrong somewhere else..
@Chew-Seong Cheong – I miscalculated, I used the diameter instead of radius for r 2 .
Let the radius of the yellow semicircle be r 1 , blue semicircle be r 2 and pink circle be r 3 . Then
r 1 + 2 r 2 = r 1 + 2 r 3 = 1 ⟹ r 2 = r 3
Also, ( r 2 + r 3 ) 2 = ( r 1 + r 2 ) 2 + ( r 1 + r 3 ) 2 ⟹ 4 r 2 2 = 2 ( r 1 + r 2 ) 2
⟹ r 1 = ( 2 − 1 ) r 2
⟹ r 2 = 2 + 1 1 = 2 − 1 , r 1 = ( 2 − 1 ) 2
Area of all the colored figures is
2 π r 2 2 + 2 π r 1 2 = 2 π ( 2 9 − 2 0 2 )
Hence, area of the required region is
2 π ( 2 0 2 − 2 8 ) = π ( 1 0 2 − 1 4 )
So, a = 1 0 , b = 2 , c = 1 4 , and
b a . c + ⌈ π ⌉ = 1 0 × 1 4 + 4 = 1 2 .
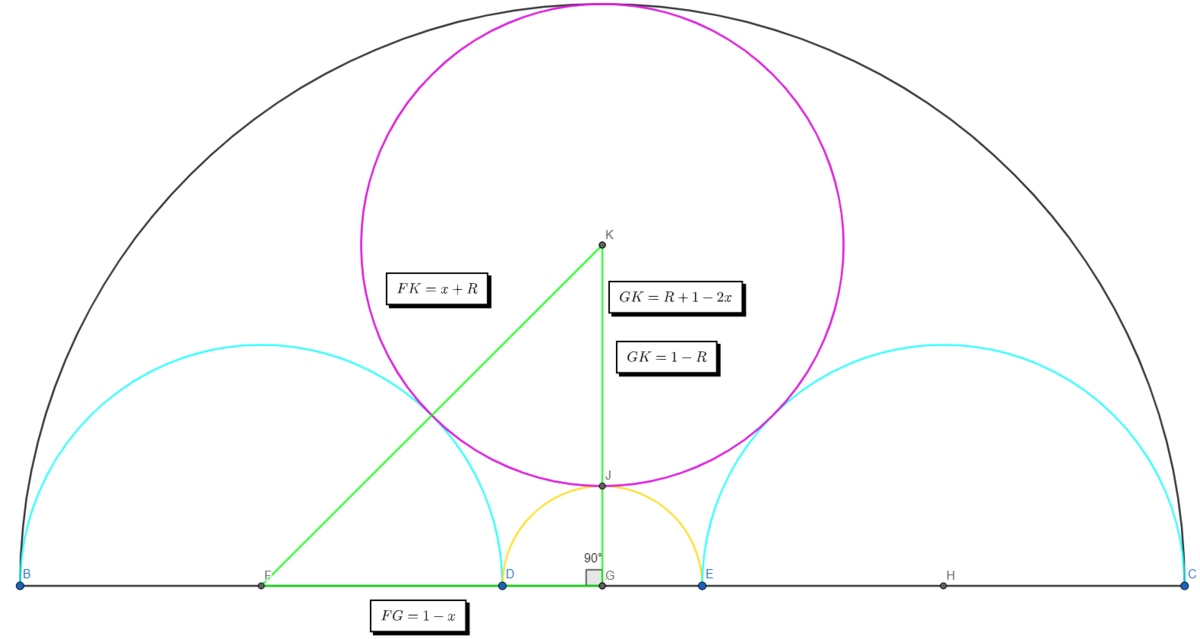
We can easily solve this problem by using the pythagorean theorem :
 -
{
(
x
+
R
)
2
=
(
R
+
1
−
2
x
)
2
+
(
x
+
1
−
2
x
)
2
R
+
1
−
2
x
=
1
−
R
-
{
(
x
+
R
)
2
=
(
R
+
1
−
2
x
)
2
+
(
x
+
1
−
2
x
)
2
R
+
1
−
2
x
=
1
−
R
- We solve this system of equation and get R = 2 − 1 and x = 2 − 1
- Then the white area is : 2 π − π ( 2 ( 2 − 1 ) 2 + 2 ( 1 − 2 2 + 2 ) 2 ) = π ( 1 0 2 − 1 4 )
- 2 1 0 ⋅ 1 4 + ⌈ π ⌉ = 1 2
Let the centers of the purple circle, the yellow semicircle and right blue semicircle be A , B , and C and their radii be r 1 , r 2 , and r 3 respectively. Points P and Q are tangent points of the purple circle and the left blue semicircle with the black semicircle. Then P B = 2 r 1 + r 2 = 1 and Q B = 2 r 3 + r 2 = 1 . This means that r 1 = r 3 . Then we note that △ A B C is an isosceles right triangle with ∠ B = 9 0 ∘ and
C A 2 r 1 2 r 1 ⟹ r 1 ⟹ r 2 = 2 A B = 2 ( 1 − r 1 ) = 1 − r 1 = 2 + 1 1 = 2 − 1 = 1 − 2 r 1 = 3 − 2 2
The area of the white region is given by:
A = 2 π − 2 π r 1 2 − 2 π r 2 2 = π ( 2 1 − 4 ( 2 − 1 ) 2 − ( 3 − 2 2 ) 2 ) = π ( 1 0 2 − 1 4 )
Therefore, b a c + ⌈ π ⌉ = 1 4 0 + 4 = 1 2 .