Mysterious points on an angle bisector
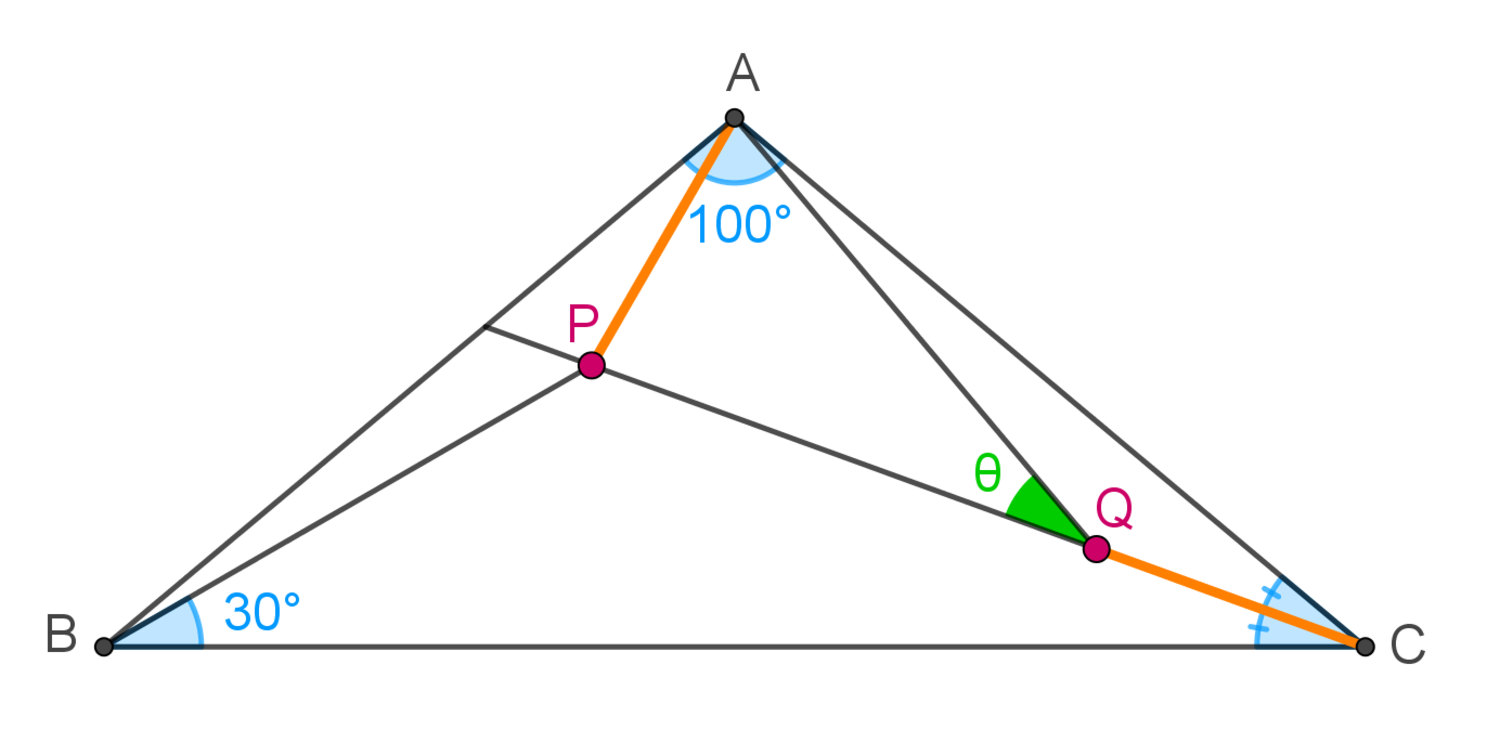 In the figure,
△
A
B
C
is isosceles with
∠
B
A
C
=
1
0
0
∘
. Points
P
and
Q
lie on the angle bisector of
∠
A
C
B
, in such a way that
∠
P
B
C
=
3
0
∘
and
A
P
=
C
Q
. Evaluate
∠
A
Q
P
in degrees.
In the figure,
△
A
B
C
is isosceles with
∠
B
A
C
=
1
0
0
∘
. Points
P
and
Q
lie on the angle bisector of
∠
A
C
B
, in such a way that
∠
P
B
C
=
3
0
∘
and
A
P
=
C
Q
. Evaluate
∠
A
Q
P
in degrees.
C h a l l e n g e : Make no use of trigonometry.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
For where you wrote A C = 2 cos 5 0 ° = 2 sin 1 3 0 ° , did you mean B C = 2 sin 5 0 ° = 2 sin 1 3 0 ° ?
Hi Mark! I cannot quite follow. Can you check any typos in " A C = 2 cos 5 0 ∘ = 2 sin 1 3 0 ∘ "? In which triangle do you use Sine Rule?
Log in to reply
Try triangle B P C , with angles 1 3 0 ∘ , 3 0 ∘ , 2 0 ∘ .
A C already corrected to B C .
Log in to reply
I believe the cos 5 0 ° that's written with B C should be sin 5 0 ° instead.
Log in to reply
@David Vreken – This will teach me to type a solution in two minutes before a lesson...
Consider Triangle BPC and its circumcenter O. Since angle BPC is 130°, its circum-radius will be CP. With BPC = 130°, arc BC should be 50 deg, and will form 100 deg at centre O. Triangle OBC is congruent to triangle ABC. Hence OC=OB=AB=AC=CP. Triangle APC is isosceles, hence angle CAP=80° and Angle PAB= 20°. Triangle BAP and ACQ are congruent. We get angle AQP=30°
Log in to reply
How do you know that if angle BPC is 130°, that its circumradius will be CP?
Log in to reply
You could say that C P subtends an angle of 3 0 ∘ at the circumference of the circumcircle of P B C , so it subtends an angle of 6 0 ∘ at the centre of the circumcircle, which means that O C P will be equilateral, and hence C P = R . This would give @Thanos Petropoulos his trig-free proof.
Log in to reply
@Mark Hennings – Okay, thanks!
@Mark Hennings – After your clarifications, it certainly does. Thanks Mark!
Also, is there a typo in OA = OB = AB = AC = CP? Should OA be OC instead?
Log in to reply
Yes, though all we need is C P = O C = A C . That A B and O B are also the same is true, but unimportant.
Thank you
@Ajit Athle
- This is a purely geometric proof. I add here a diagram which hopefully visualizes your idea. Perhaps, instead of “Since angle BPC is 130°” it should say “”Since angle PBC is 30°, angle POC is 60°” as
@Mark Hennings
has commented.
@David Vreken
is also right, there is a typo in “OA = OB = AB = AC = CP”: instead of OA it should be OC.
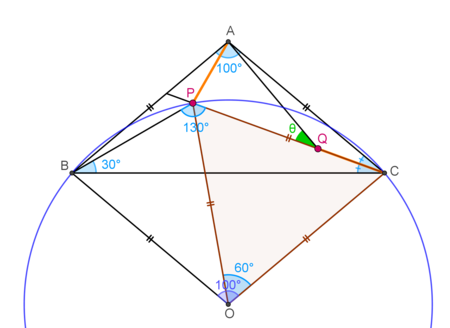
Thanks Thanos
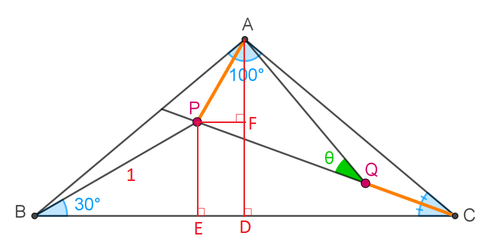
Let A D and P E be perpendicular to B C , P F perpendicular to A D , and B P = 1 . Then P E = B P ⋅ sin 3 0 ∘ = 2 1 and B E = B P ⋅ cos 3 0 ∘ = 2 3 . And
B C ⟹ B D P F A D A F tan ∠ P A F ⟹ ∠ P A F = B E + E C = 2 3 + P E ⋅ cot 2 0 ∘ = 2 3 + 2 1 tan 7 0 ∘ = 2 3 + 2 ( 1 − 3 t ) 3 + t = 1 − 3 t 3 − t = 2 B C = 2 ( 1 − 3 t ) 3 − t = E D = B D − B E = 2 ( 1 − 3 t ) 3 − t − 2 3 = 1 − 3 t t = B D ⋅ tan 4 0 ∘ = B D ⋅ cot 5 0 ∘ = 2 ( 1 − 3 t ) 3 − t ⋅ 3 − t 1 + 3 t = 2 ( 1 − 3 t ) 1 + 3 t = A D − F D = A D − P E = 2 ( 1 − 3 t ) 1 + 3 t − 2 1 = 1 − 3 t 3 t = A F P F = 3 t t = 3 1 = 3 0 ∘ Let t = tan 1 0 ∘
This means that ∠ B A P = ∠ B A D − ∠ P A F = 5 0 ∘ − 3 0 ∘ = 2 0 ∘ . Then △ A B P and △ A C Q are congruent and ∠ C A Q = ∠ A B P = 1 0 ∘ . And ∠ A Q P = ∠ C A Q + ∠ A C Q = 1 0 ∘ + 2 0 ∘ = 3 0 ∘ .
Another ingenious solution! Yet, I challenge you to a solution without trigonometry.
This is more so a solution sketch rather than a solution, but I tried to solve it without the use of trigonometry.
The crucial claim is that △ A Q C ≅ △ B P A . We have information that A C = A B and A P = Q C . If we determine that ∠ B A P = ∠ A C Q or B P = A Q , then we determine that the triangles are congruent.
If we can prove that these triangles are congruent, we can deduce that ∠ B A Q = 9 0 ∘ . Combined with the fact that ∠ A P Q = 6 0 ∘ , then we can show that θ = 3 0 ∘ .
How do you know that ∠ A B P = ∠ C A Q ?
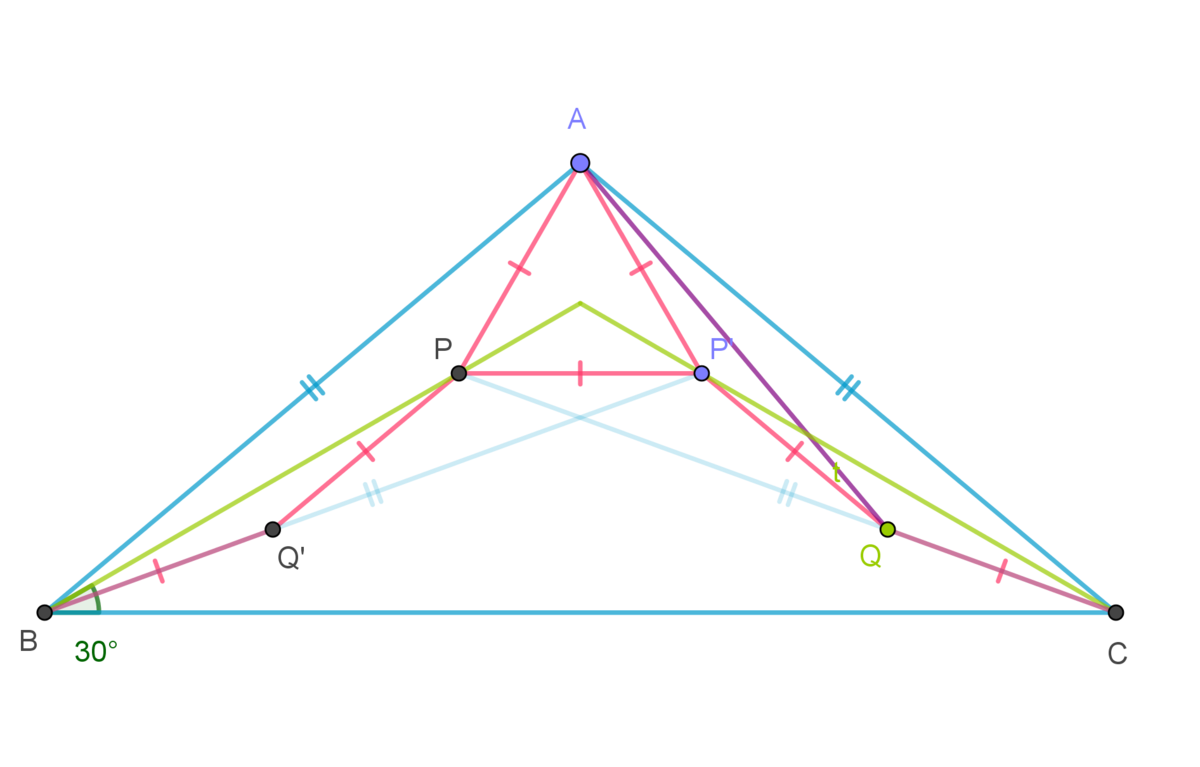

Suppose that A B = A C = 1 . Then B C = 2 sin 5 0 ∘ = 2 sin 1 3 0 ∘ and so, using the Sine Rule, P C = 2 sin 3 0 ∘ = 1 . Thus A P C is isosceles, and hence ∠ A P C = 8 0 ∘ , ∠ A P B = 1 5 0 ∘ . and hence ∠ P A B = 2 0 ∘ . Thus we deduce that triangles P A B and Q C A are congruent, and hence ∠ A Q C = 1 5 0 ∘ , so that θ = 3 0 ∘ .