N-gonal Truncated Pyramids.
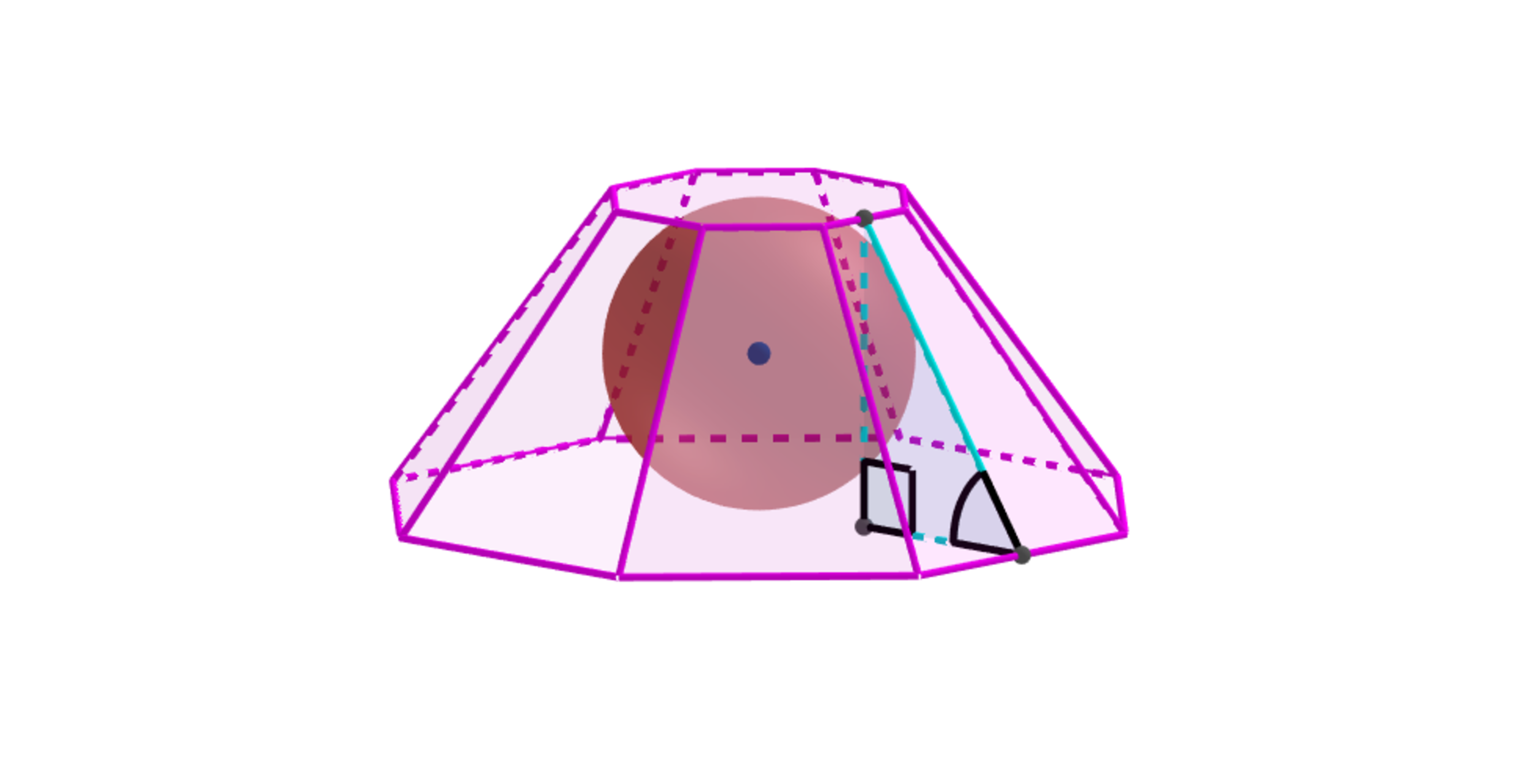
In the diagram above, a sphere is inscribed in a n -gonal truncated pyramid such that the volume of the n -gonal truncated pyramid is twice the volume of the sphere.
Let θ ( n ) be the slant height angle of the n -gonal truncated pyramid.
Find lim n → ∞ θ ( n ) in degrees.
Note: My intention is to use the n -gonal truncated pyramid not a truncated cone.
The answer is 63.43494882.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
For a truncated cone, this angle is 5 7 . 4 6 5 7 7 ° . Why is the difference?
Log in to reply

I recently did a problem where a sphere is inscribed in a truncated cone such that the volume of the truncated cone is twice the volume of the sphere.
You were asked to find the measure of the slant height angle(in degrees) and the measure of the angle is the same, I.E; 6 3 . 4 3 4 9 4 8 8 2 ∘ .
My solution is below:
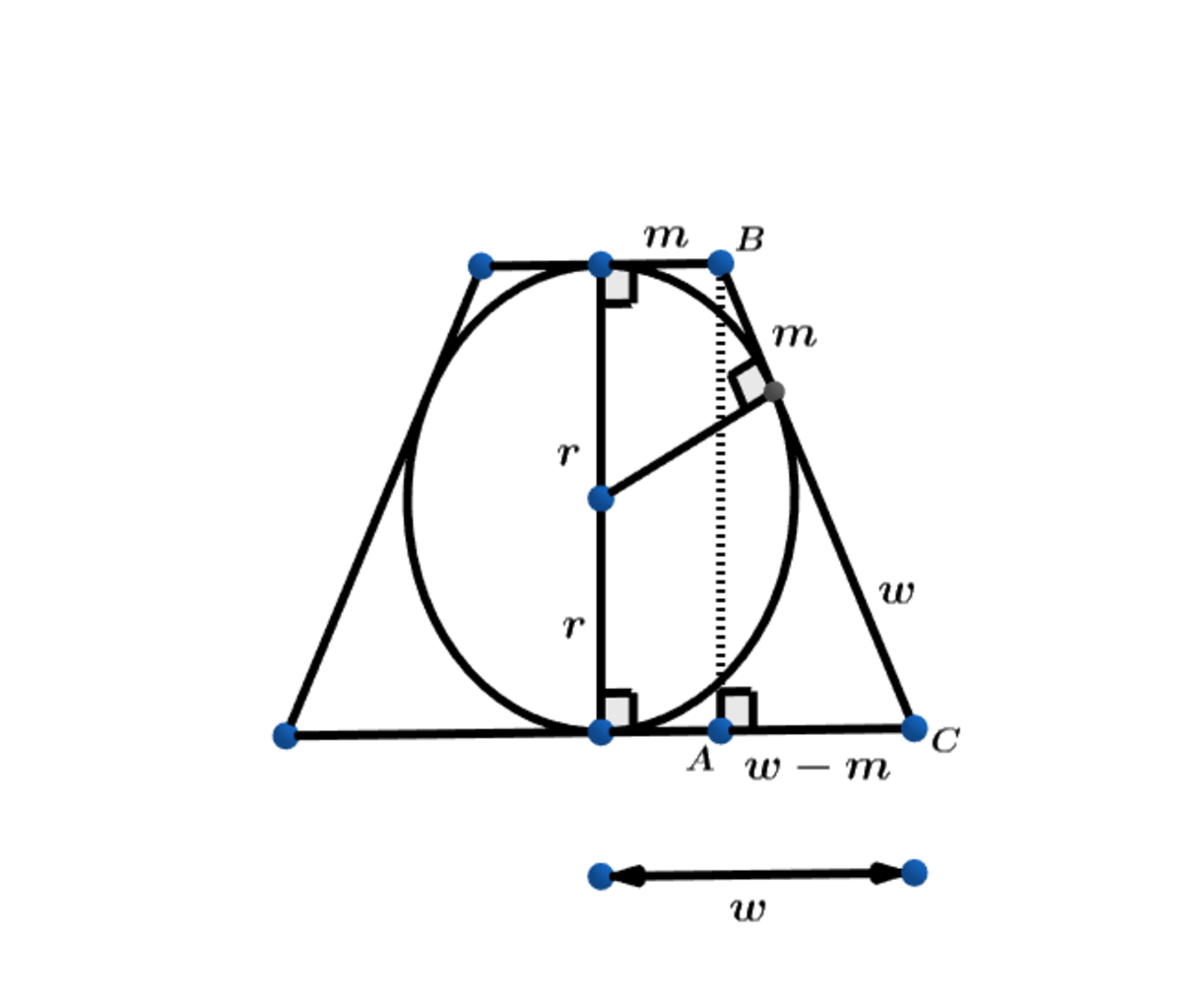
Using the fact that tangents to a circle from an outside point are congruent we obtain the diagram above.
The height h of the truncated cone is h = 2 r
Using right △ A B C we have:
( w + m ) 2 = ( w − m ) 2 + 4 r 2 ⟹ w 2 + 2 w m + m 2 = w 2 − 2 w m + m 2 + 4 r 2 ⟹ 4 w m = 4 r 2 ⟹ r 2 = w m ⟹
r = w m .
The volume of the inscribed sphere V s = 3 4 π ( w m ) 2 3
and
The volume of the truncated cone is V T = 3 2 π ( w 2 + w m + m 2 ) ( w m ) 2 1
V T = 2 V s ⟹ w 2 + w m + m 2 = 4 w m ⟹ w 2 − 3 w m + m 2 = 0 ⟹ w = ( 2 3 ± 5 ) m
Since m w > 1 we choose w = ( 2 3 + 5 ) m ⟹ cos ( θ ) = w + m w − m = 5 + 5 1 + 5 = 5 1
⟹ θ ≈ 6 3 . 4 3 4 9 4 8 8 2 ∘ .
Log in to reply
OK, thanks.
Log in to reply
@A Former Brilliant Member – No problem.
Log in to reply
@Rocco Dalto – Keep continuing the series. It's interesting. :)
△ A B C ∼ △ D B E ⟹ H ∗ x = H ∗ − H y ⟹ ( x − y ) H ∗ = x H ⟹ H ∗ = x − y x H
⟹
Volume of truncated pyramid V T ( n ) = 1 2 n cot ( n π ) ( x 2 ( x − y x H ) − y 2 ( x − y x H − H ) ) =
1 2 n cot ( n π ) ( x − y x 3 − x y 2 + x y 2 − y 3 ) H = 1 2 n cot ( n π ) ( x 2 + x y + y 2 ) H .
Using the fact that tangents to a circle from an outside point are congruent we obtain the diagram above.
The height H of the truncated cone is H = 2 r
Using right △ A B C we have:
( w + m ) 2 = ( w − m ) 2 + 4 r 2 ⟹ w 2 + 2 w m + m 2 = w 2 − 2 w m + m 2 + 4 r 2 ⟹ 4 w m = 4 r 2 ⟹ r 2 = w m ⟹
r = w m .
The volume of the inscribed sphere V s ( n ) = 3 4 π ( w m ) 2 3 .
The volume of the truncated n - gonal pyramid is:
V T ( n ) = 3 2 n tan ( n π ) ( w 2 + w m + m 2 ) ( w m ) 2 1
V T ( n ) = 2 V s ( n ) ⟹ w 2 + w m + m 2 = n 4 π cot ( n π ) w m ⟹
w 2 − ( n 4 π cot ( n π ) − 1 ) w m + m 2 = 0
For n ≥ 3 :
Let s ( n ) = n 4 π cot ( n π ) − 1
( 0 < s ( n ) < 3 ) and s ( n ) is monotonic increasing for n ≥ 3 and lim n → ∞ s ( n ) = 3
To show: lim n → ∞ s ( n ) = 3
To show: lim n → ∞ n sin ( n π ) = π
Using the inequality: cos ( u ) < u sin ( u ) < 1 ⟹ cos ( n π ) < n π sin ( n π ) < 1 ⟹
π cos ( n π ) < n sin ( n π ) < π and π lim n → ∞ cos ( n π ) = π ⟹ lim n → ∞ n sin ( n π ) = π
⟹
4 π lim n → ∞ n cot ( n π ) = 4 π 2 lim n → ∞ n 2 csc 2 ( n π ) =
4 π 2 lim n → ∞ ( n sin ( n π ) ) 2 1 = 4 π 2 ( π 2 1 ) = 4
⟹ lim n → ∞ s ( n ) = 3 .
w 2 − ( n 4 π cot ( n π ) − 1 ) w m + m 2 = 0 ⟹
w ( n ) = ( 2 n 4 π cot ( n π ) − 1 ± ( n 4 π cot ( n π ) − 1 ) 2 − 4 ) m = ( 2 s ( n ) ± s ( n ) 2 − 4 ) m
m w 1 ( n ) = 2 s ( n ) − s ( n ) 2 − 4 < 2 3 − 5 < 1
and
m w 2 ( n ) = 2 s ( n ) + s ( n ) 2 − 4 > 2 3 + 5 > 1
Since m w > 1 we choose w ( n ) = w 2 ( n ) = ( 2 s ( n ) + s ( n ) 2 − 4 ) m
⟹ lim n → ∞ w ( n ) = 2 3 + 5 m
Let cos ( θ ( n ) ) = w ( n ) + 1 w ( n ) − 1
⟹ lim n → ∞ w ( n ) + m w ( n ) − m = 5 + 5 1 + 5 = 5 1 = cos ( θ )
⟹ θ = 6 3 . 4 3 4 9 4 8 8 2 .