Nātīvitās Geoculus
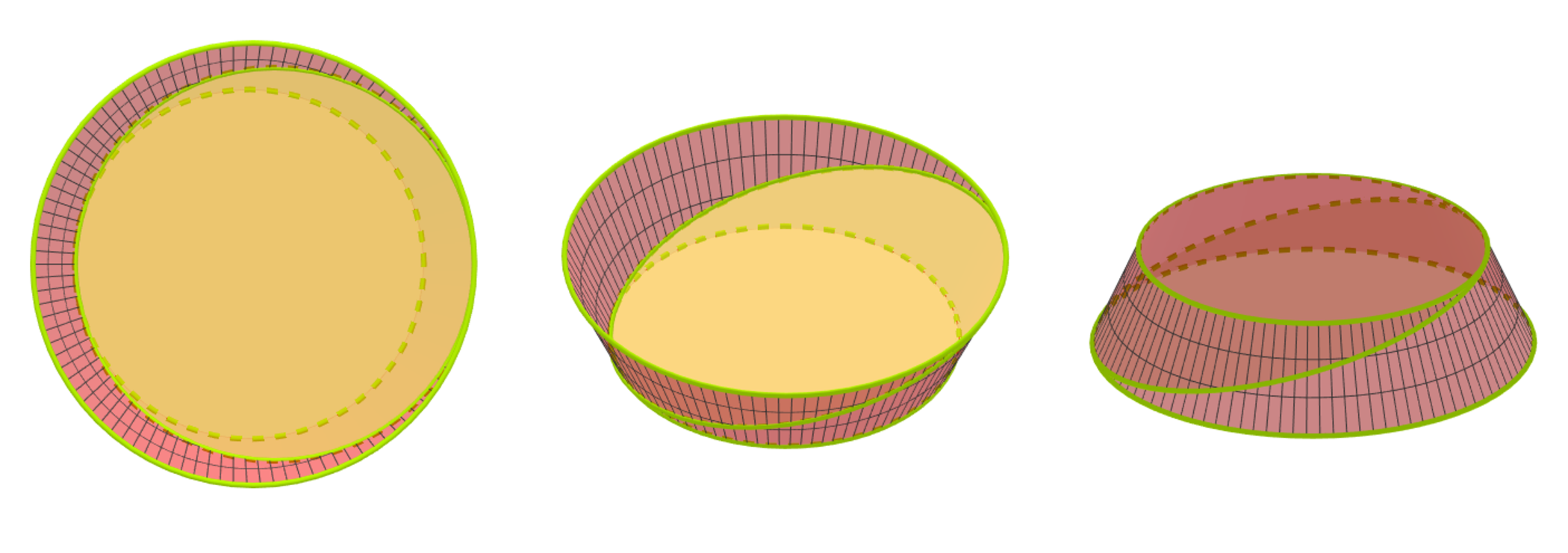
Inside the warm mansion, while delivering tons of presents to the children, Santa Claus became thirsty and hungry, so he took some break to help himself some delicious snack. After some minutes of searching, he found a very large caramel cookie in the shape of an ellipse whose semi-major and semi-minor are respectively 2 5 cm and 2 4 cm . He also found a series of bowls and a very large container of milk. Since Santa enjoys drinking and dipping, he poured a milk into a bowl in the form of a right-angle conical, circular frustum, satisfying the following conditions:
- As shown above, when the cookie is dipped, its circumference is tangent to the inner surface, including two opposite ends of the circular bases.
- The volume of the milk is the maximum.
If that volume is V π cm 3 , input ⌊ V ⌋ as your answer.
Assumption: Neglect the thickness of the cookie.
The answer is 8064.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
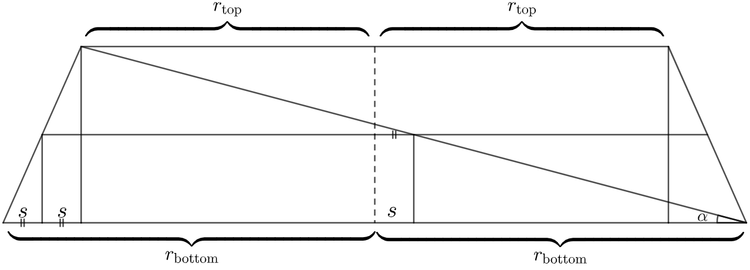
Let a denote the semi-major and b the semi-minor. Consider the isosceles trapezoid, the cross-section orthogonal to the circular bases r top and r bottom , and the angle α formed by the diagonal and one of the circular bases. Since b = r top r bottom for the cross section to exist within the right-angle frustum (left that as the Sangaku exercise), condition r top ≤ r bottom . Then, since the minor axis of the ellipse exists as the chord of the circular cross section of the radius 2 1 ( r top + r bottom ) , by the Pythagorean Theorem ,
s = ( 2 1 ( r bottom + r top ) ) 2 − ( r top r bottom ) 2 = 4 1 ( r top ) 2 + 4 1 ( r bottom ) 2 − 2 1 r top r bottom
which shows that
Diameter of the bottom base Diameter of the top base = 2 r bottom = 2 r top = 2 a cos α + 2 4 1 ( r top ) 2 + 4 1 ( r bottom ) 2 − 2 1 r top r bottom = 2 a cos α − 2 4 1 ( r top ) 2 + 4 1 ( r bottom ) 2 − 2 1 r top r bottom
Using the following volume formula of a frustum,
Volume = 3 1 h ( A 1 + A 2 + A 1 A 2 )
where
- h = 2 a sin α denotes the height of the trapezoid
- A 1 = π ( r top ) 2 denotes the area of the top circular base
- A 2 = π ( r bottom ) 2 denotes the area of the bottom circular base
using what we already know about the frustum and the given cross section, we obtain
Volume = 3 2 π a sin α ( 3 a 2 cos 2 α + 4 1 ( r top ) 2 + 4 1 ( r bottom ) 2 − 2 1 r top r bottom ) = 3 2 π a sin α ( 3 a 2 cos 2 α + 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ) = 3 2 π a 2 − ( r bottom − 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ) 2 ⎝ ⎛ 3 ( r bottom − 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ) 2 + 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ⎠ ⎞
where a 2 ≥ ( 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ) 2 . But that suggests the frustum "vanishes" at the positive upper bound r bottom = a + a 2 − b 2 , following b = r bottom ( 2 a − r bottom ) (illustrating the ellipse of the fixed axes overlaps both circular bases).
As a 2 − ( r bottom − 4 ( r bottom ) 2 b 4 + 4 1 ( r bottom ) 2 − 2 b 2 ) 2 = 0
for r bottom = a + a 2 − b 2 , the height is decreasing and continuous at b ≤ r bottom ≤ a + a 2 − b 2 , involving AM-GM Inequality . With some algebraic and calculus calculation (as the derivative of V is nonpositive at that interval), it achieves its maximum at r bottom = b , yielding a cylinder of the volume V max = 2 π b 2 a 2 − b 2 for a = 2 5 and b = 2 4 .
In this case, V max = 8 0 6 4 π , where ⌊ V ⌋ = 8 0 6 4 .
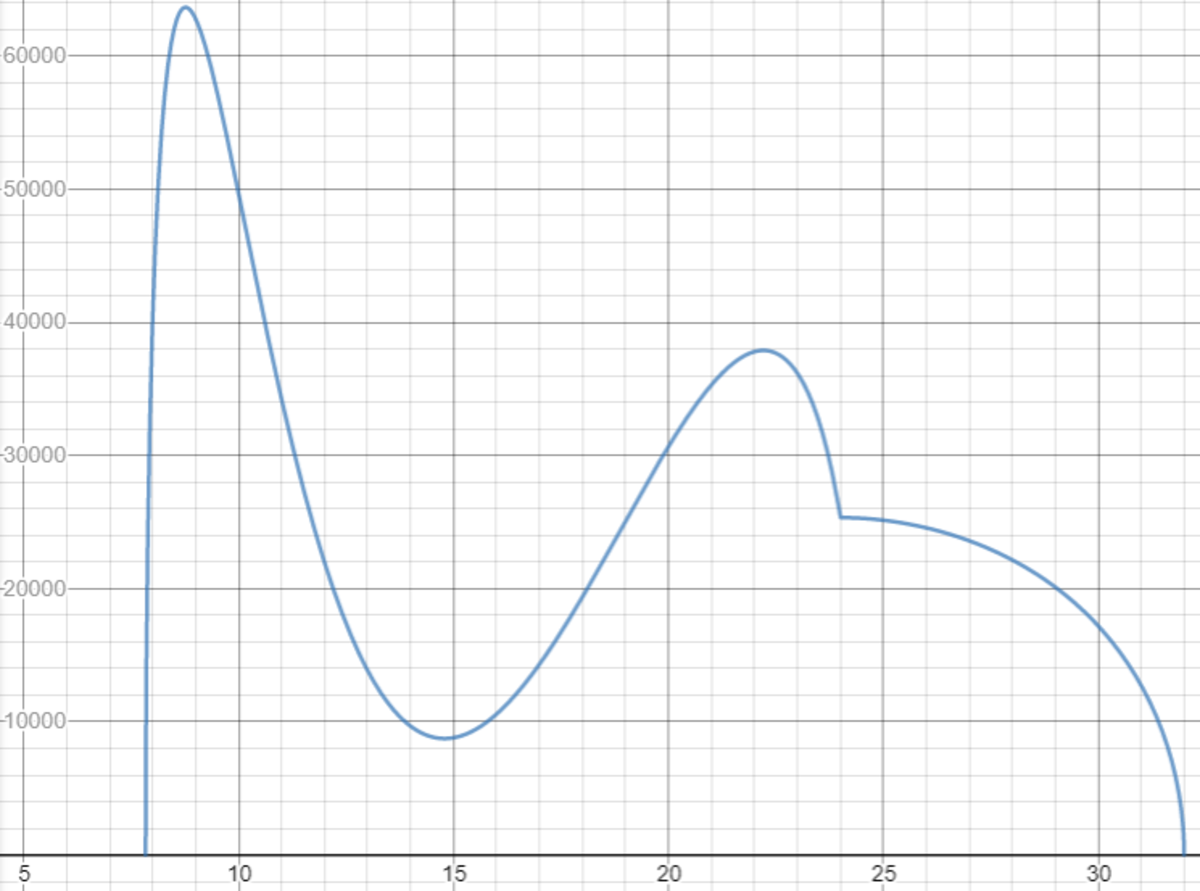
The graph above illustrates the idea of the volume equation in the Cartesian plane. While it has maxima at r bottom < b , they do not satisfy the condition b = r top r bottom needed to solve the problem.
Last, but not least, Merry Christmas!
Hi
Due to brilliant's awesome support for direct messaging I'm here.
I'm no longer active on brilliant and feel kinda sad at the loss of the community it was before.
Do you have other social media that you are comfy with sharing?
Log in to reply
Hello, Julian! Long time no see! It has been a long while since I was out from Brilliant! I have some social media, including Discord. Let me know which one you are using.
Log in to reply
Hello! I open brilliant only when Miss Chrome™ reminds me of it's existence., hence replying so late. My discord is
Free food#9020
Log in to reply
@Julian Poon – Done. I have sent the friend invitation message to you. Please check when you can.
Extend the sides of the bowl to make a cone, and label the diagram as follows (where the cookie is D F ):
By alternate interior angles, α = ∠ B F G = ∠ F E G , and by corresponding angles, β = ∠ A F B = ∠ F I C .
By properties of a conic section , the eccentricity is e = cos β cos α = 1 − a 2 b 2 = 1 − 2 5 2 2 4 2 = 2 5 7 . Therefore, cos α = 2 5 7 cos β .
From △ B F D , the height of the frustum is C G = 5 0 cos α = 1 4 cos β .
From △ C D I , one radius of the frustum is C D = I D sin β and the height of the cone is C I = I D cos β .
Since G B = C B − C G = I D cos β − 1 4 cos β , from △ G H I , the other radius of the frustum is G H = ( I D − 1 4 ) cos β .
By the law of sines on △ F D I , I D = sin 2 β 5 0 sin ( 1 8 0 − α − β ) = sin β 2 5 sin α + cos β 2 5 cos α . Substituting cos β cos α = 2 5 7 from above gives I D = sin β 2 5 sin α + 7 .
The volume of the frustum is V = 3 1 ⋅ π ⋅ C G ( C D 2 + G H 2 + C D ⋅ G H ) . Substituting the above values and simplifying gives V f = 3 5 6 π ( 4 8 1 cos β − 4 9 cos 3 β ) .
Since the derivative of 4 8 1 cos β − 4 9 cos 3 β with respect to cos β is 4 8 1 − 1 4 7 cos 2 β , and 4 8 1 − 1 4 7 cos 2 β > 0 for all possible values of cos β , the volume increases as cos β increases, and the maximum volume is when cos β is a maximum at cos β = 1 . (In other words, when the frustum is a cylinder.)
The maximum volume is then V f = 3 5 6 π ( 4 8 1 ⋅ 1 − 4 9 ⋅ 1 3 ) = 8 0 6 4 π , so ⌊ V ⌋ = 8 0 6 4 .