NBA Championships or the Stanley Cup?
Professional sports leagues usually do their best to even the playing field by distributing skilled players throughout the league. This way, teams are always competitive and the games are more fun to watch.
Still, teams are always a bit uneven in terms of skill level, or scoring potential. Throughout the 2018 NBA season, the Cleveland Cavaliers and the Golden State Warriors have scored an average of 101 and 109 points per game, respectively and are facing each-other in the NBA Championship. In the NHL, the Washington Capitals and the Las Vegas Knights scored an average of 3.12 and 3.26 goals per game, respectively and are facing each-other in the Stanley Cup.
An example basketball scoreboard.
Which underdog team is more likely to win their respective championship?
Details: Assume the teams' defensive performance is comparable and use only the provided points-per-game statistics. In hockey, a goal counts as one point; in basketball, goals count as either one, two, or three points depending on how it was made.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Agree with you about coins analogy and sample size importance, but I would argue that points in basketball and goals in hockey are somewhat hard to compare. This comes from the fact that in hockey every goal is worth 1 point, while that's not the case in basketball. According to this logic, we should take into account baskets-per-game rather points-per-game and thus our approximation shouldn't be flipping coin 200 times (approximate total number of points) but instead only, say, 100 times (approximate total number of shots) as you've done but didn't explicitly mention. However, the problem arises when one team has a higher points-per-basket ratio. For example, Warriors are generally better three-point shooters than Cavaliers as they have players like Steph Curry, Klay Thompson and Kevin Durrant. This drives their points-per-basket up which helps them win a game even though they scored less baskets.
Anyway, the final conclusion that Washington Capitals are more likely to win the championship still remains.
Apologize if this is a silly question, but was there a quick way you deduced P(heads) = 0.48 and P(tails) = 0.52 ? After staring at the wall for a few minutes, I had to set up a system of equations and solve: H + T = 1 and T - H = 0.08 H, where H = P(heads) and T = P(tails).
Log in to reply
You probably got a bit more accurate answer than me! I knew the probabilities would be split roughly 50:50, and that the difference between the two probabilities would be 8 % . And since 8 per 100 is 4 per 50, I figured the split would be pretty damned close to 0.04, and so came up with 0.48 and 0.52.
The real answer is a bit different: 0 . 4 8 0 7 and 0 . 5 1 9 3 .
Your problem requires at places more inside American knowledge, than it does mathematics. The runnings Basketball is not self-understood for the rest of the planet. So it would be nice if these were explained.
- Does the problem refer to the image or is that just cosmetic?
- What does B mean?
- Is 13:37 just the time, or how many minutes have elapsed?
- What is Quarter 2? Does it mean they’re currently in the 2nd quarter and the scores represent the state of things at the end of the 1st? Or does it mean they’ve just ended the 2nd quarter? Or does it mean the quarter finals?
Given that background understanding has been cleared up, how does average performance weigh in on the remainder of the game? Does it hold that E [ Score ∣ Score 1st quarter = x ] = x + 4 3 ⋅ E [ Score ] ?
Log in to reply
Hi there-
The image is just a basketball scoreboard serving as an illustration. Purely cosmetic. The problem states that it should be answered using only the provided points per game statistics. I'm happy to try to answer your questions about the scoreboard, but this is little more than a stock image that's on topic and has nothing to do the the question. We're concerned only with the statistics of small numbers, and observing that the number of scoring events is far fewer in hockey than basketball (based on the points per game statistics).
Re: the scoreboard: I am not American, and not much of a basketball fan, but I believe B is some bonus related to number of free throws a team gets for a foul.
13:37 is a randomly chosen number, I believe it is the remaining time in a basketball scoreboard (15 min per quarter).
I believe quarter 2 indicates that the game is currently in the 2nd quarter, with the indicated time remaining in that quarter. The score is generally updated in real time as points are scored.
The answer to your expectation value question depends on how we model the game. But for this question we're just concerned with the final score (which team wins) and the only prior knowledge to be used is the historical points per game performance of the teams.
Of course, this is a simple model, and I'd love to hear your thoughts on how you'd model the expected score in real time as the game evolves.
Cheers.
Log in to reply
Thanks for you reply. It really was for me a bit confusing. As you can see from my questioning it’s not clear whether or not the data in the image falls under the game statistics —I’m no sports fan, but don’t the data during a match count as statistic (albeit not summarising statistics)? Perhaps you should post with a caption to make this clear, eg
 Fig 1. An example of points during a game.
Fig 1. An example of points during a game.
Or place this at the start?
If the averages are 1 0 1 vs 1 0 9 , there’s not really much to think about (beyond that the defences are comparable) to conclude that the team with the higher average is ‘expected’ to win. The only part to think about is how strongly justified the conclusion is (hypothesis testing, etc.).
It would make for a future basic problem if you gave a statistic about average points scored per minute, say, and then really to use live data in the middle of a match to then ask what the expected outcome would be, as the live data could swap things around. Otherwise it’s just 1 0 1 < 1 0 9 therefore the team with the larger average wins.
Okay, now I finally (sort of?) get the problem. I’m seriously confused by the text. The data are:
- There are 4 Teams: CC, GSW, WC, LK
- CC vs. GSW in one sport (NBA) rack up an average of 101 : 109 points per game (against each other?)
- WC vs. LK in another sport (NHL) rack up an average of 3.12 : 3.16 points per game (against each other?)
- Now CC plays against WC … even though NHL ≠ NBA are completely different sports
- Task: who will win on average?
You can see that this makes no sense. I’m relaying what the brain does with a lack of further clarification .
Clearly, going on the solutions posted here, the last two points above are wrong. I should interpret the problem as saying something like:
- You have the chance place bets on the underdog in at exactly 1 of the sporting championships.
- On which sporting event should you bet on the underdog, to have the highest changes of winning? Ie Which underdog team is more likely to win their respective championships?
And then you do the whole percentage leads comparison. Without those words (and because of the image), I thought at first, you’re just talking about the NBA teams … then my second take, triple reading the names of teams, two of which are easy to confuse… I got to the above interpretation. I know obviously there cannot be two underdogs in one sport, but coupled with the other confusions, this contradiction was not enough to get at the right interpretation. Maybe it’s just me, but you can clearly see, that it took a number of attempts to get at the right interpretation (second list of points). The problem is not difficult to understand, but framing is (at least for me).
Log in to reply
I've reworded the problem a bit to address some of the confusion you mentioned. I'll also try to make less ambiguously framed problems in the future. Cheers!
Surely these chances to win the league reflect the probability at the start of each season but the statistics provided require that we must be partway through the season. The chance to win the league will also depend on how far into each season we are thus indicating the current league scores. It will also depend on the length of each season to determine the number of remaining games. It will further depend on the number of league points gained or lost for wins, losses and draws. Ultimately if one season has a single game remaining and a deficit greater than the points available there is a zero chance to win the league whilst the other league may only just have started and so there would be a finite probability of winning. We also are not given the statistics for all the other teams so whilst we may be able to predict the probability of the the orderings of the two pairs of teams I can't see how this would determine whether any of them would win their respective league championship.
Log in to reply
hey Craig-
The pairs of teams in each sport were selected because they are facing each-other in the Championships this week. So they've already made it through the season and these statistics reflect the season average.
Sorry I realize that wasn't entirely clear, I've updated the problem.
This is a nice explanation, Blake, and I totally agree, given the question. However, there is a problem with the original question which your example assumes the answer: variance. In your example of the biased coin, you are also defining its variance and standard deviation, because we all know how coins (even biased coins) work.
Given only this statement, "the Cleveland Cavaliers and the Golden State Warriors have scored an average of 101 and 109 points per game, respectively," it is mathematically possible that the Warriors score exactly 109 points every single game, but the Cavs score 110 points in nine out of every 10 games, but only 20 points in one out of every 10. Therefore, the mostly hot but occasionally ice cold Cavs have a 90% chance of beating the ploddingly consistent Warriors.
1 0 1 1 0 9 ≈ 1 . 0 7 9 2 so the Cavaliers get outscored by about 8%. 3 . 1 2 3 . 2 6 ≈ 1 . 0 4 4 9 so the Capitals only get outscored by about 4.5%. Knowing nothing about the distributions of scores (and how ties are broken in hockey), I figure the Capitals have a better chance.
Would you expect the answer to change if for example, the Knights averaged 3.43 points per game? That would make the Capitals outscored by about 1 0 % compared to the 8 % that the Cavaliers get outscored by based on your calculations.
Michael's analogy to biased coins works perfectly here. You have two unfair coins; one that has a 1 0 % higher chance of coming up tails than heads, and one that has an 8 % higher chance of coming up tails than heads.
In which scenario would you rather bet on the underdog result? Getting more heads than tails on 5 rolls of the 1 0 % coin, or getting more heads than tails on 200 rolls of the 8 % coin?
Log in to reply
Is a coin flip analogy relevant here? We have no information about the distribution of scores. In a sense don't know what 3.26 goals even means. Do they take 4 shots in a game or 100? If they take roughly the same in basketball, my reasoning seems reasonable to me.
Log in to reply
The biased coin flip analogy is relevant here, and would give the same result as your reasoning if there were the same number of scoring events in hockey and basketball .
If this were the case, then indeed your answer would make perfect sense. For example, in basketball a field goal is 2 points, and a three-pointer is 3 points. If scores in hockey were some small fraction of a point (~0.1), we could assume similar distributions of scores between the games even though the average points per game for hockey are ~3 and the average points per game for hockey are ~100. With the same number of "coin flips"/events, you'd definitely bet on a biased coin with a more favourable bias.
But really there are rarely any more than a handful of goals in a hockey game, while there are on the order of 100 in most basketball games. The "points per game" statistics were intended to hint towards this much lower number of "scoring events" for hockey. When a team can only score in increments of 1, and the average per game is ~3, there are some pretty serious inferences you can make about the distribution of scores. In this case you'd probably choose the coin more biased against you that you only had to win best of 5 events/flips, rather than the slightly less biased coin that you had to win best of 100 events/flips.
We are provided no information at all about the variance of the statistics. We are not told that they are distributed like binomial variables. They could all be normally distributed and the answer would still depend on the variances.
Given the nature of the games, it's likely that the variances in basketball scores are much lower as a percentage of the mean than is true for hockey.
It's useful that the means are relatively closer in hockey than basketball. l would hate to have to figure out the break-even point on the fly.
Interesting. I put the smaller number on top like 101/109. Doing so I got 92% and 95%, thus obtaining the correct answer
I chose Capitals using same approach.
I did essentially the same thing: multiplied the 1st fraction by 3 and the 2nd fraction by 100 to get 327/303 vs. 326/312. Since 327 is very close to 326 (comparing numerators) but 312 is comparatively greater than 303 (comparing denominators) I “guesstimated” that the Capitols had the better chance.
Log in to reply
This was also my analysis, however, it is at best a guess. Further information needed is a "standard deviation." But, given the information at hand this is the best we can do.
Log in to reply
A lot of people seem to be comparing the percent "out-scored" each underdog team is. How would you approach the problem if both teams were outscored by the same percent? ie. if the basketball team records were 101-109 and the hockey were 3.36 - 3.12? If this is the only information you have, which sport's underdog would you bet on?
The goal of this problem isn't to compare percents, but to consider the differences between the statistics of small and large numbers. I really wanted to use real-world numbers for each team's scoring record, but now I'm sure I should have just made up numbers that didn't lend themselves to comparing percent outscored.
It's like you have a coin that's biased against heads, say, only 40% chance of coming up heads. Your friend wants to bet even money that you'll get tails. You know you have to play your friend at least once. How many times do you want to keep flipping? If you play it just a few times, you've got a decent chance of coming out ahead, even though it's less than 50% of that happening. If you play a hundred times, you're a sure bet to lose your money. That's how casinos reliably make their money.
I think you slightly misunderstood the premise of the answer. You should have compared relative size, not literal magnitude.
Log in to reply
We can fix that by changing the rules of the coin game slightly....after so many flips, whoever is ahead wins, so that either one or the other is the winner. So... how many times should the guy with the bad coin flip? How many times would YOU flip---a few times or a hundred times?
Log in to reply
Fine, then answer this question: Sport A average scores: 101; 109. Sport B average scores: 1111; 1112 Which underdog has a higher chance of winning?
Log in to reply
@Marc Moncada – If we stick to biased coins, your question can be modelled with the Binomial distribution.
For a biased coin with heads probability 1 0 1 + 1 0 9 1 0 1 :

The probability of heads winning out of 100 flips is about 0 . 3 1 .
For a biased coin with heads probability 1 1 1 1 + 1 1 1 2 1 1 1 1 :

The probability of heads winning out of 1000 flips is about 0 . 4 8 1 7 .
So in this case the coins (or scoring records) being so close overcame the more narrow distribution of more flips/scoring events. In my solution I show that the percent scoring advantage that a hockey team would need to overcome the low number statistics would be about 6 0 % rather than the 5 − 1 0 % that we see in the problem.
The ratio 3.12/3.26 is closer to 1 than 101/109. Therefore the Capitals is more competitive against its rival than Cleveland is to the Warriors. LET`S GO WARRIORS! 😁
Just think about this critically. The point differential between WSH and LVK is much closer than that of GSW and LeBron's Cavalier's. The chance of Washington winning is hugher considering how even both NHL teams are point wise.
This method of course looks at the numbers and doesn't consider factors such as LeBron James's immense skill and the simple fact that Ovechkin will never win a Stanley Cup.
I cheated; as a hockey fan, I already knew the answer. Mauboussin’s Skill-Luck Continuum, based on statistics, explains that hockey introduces more randomness into game results. In hockey language, it’s called “Puck Luck”. Basketball has far less randomness. Read & watch this article & video for the explanation: https://www.vox.com/videos/2017/6/5/15740632/luck-skill-sports
😁👍
Assume all the teams score follow a normal dist N(u, s i g m a ) ; NBA team always scores above 60 points per game
- by normal dist properties
3s is about equal to 101 - 60 for cavaliers; and 3s is about equal to 3.12 for capitals
s = 13.67 for cavaliers; s = 1.04 for capitals
Then Pr[ Z > (109-101)/13.67 = 0.585] < Pr[ Z > (3.26-3.12)/1.04 = 0.1346]
So Capitals has higher chance than Cavaliers
I went strictly by the percentage difference in scoring...
I find (most of?) the solutions offered here unsatifactory, mainly because they bring in assumptions that were not stated in the problem description (such as assumptions about distributions). Maybe it was not a good problem.
My reasoning was as follows. Considering an average of 3.12 and the fact that all scores are natural numbers, it is clear that this team must have played games with final scores of 4 or more. Similarly, a team with an average of 3.26 must have played games with final scores of 3 or less. Thus, the undrdog here has a fair opportunity to win. For a team with an avrage of 101, for all we know, all their games could end with 101 points. Similarly for an average of 109. Hence, the underdog would have no chance to win.
On the other hand, if the average ot 109 was achieved by 99% of their games ending with 100 points and 1% of them with 1000 points (I know little about basketball :-), then the underdog has a 99% chance of winning. So, without further assumptions, the problem does not seem solvable.
Hochey team have to go throughout shoter adversity, 109/101 = 1.079 = 8% Cavs outscored range. 3.26/3.12= 1.045= 4% Capitals outscored range. This mean they have a better chance to win.
Warriors score 8% more (on average) than Cavs, even when in basketball there are 3 point goals, Cavs would need 3 more triples on average to win over Warrios. On the other hand, Knights score 4% more (on average) than Capitals and provided the fact that both score about 3 goals per game, the Capitals just need 1 goal on average to win over the Knights. Even if we assume that it is "more difficult" to score on hockey, for the overall result of the match, one goal weights more on a hockey game than a goal on a basketball game.
☢️ Too silly solution for the philosophical minds... ☢️ My solution is a really very simple.
As we know the Las Vegas nights and the Golden state Warriors have the better odds to win the Championship in their respective sport.
We can use simply the unitary method Basketball----corresponds to-----Hockey 109-----corresponds to------3.26 101-----corresponds to------3.021
Hence we can see 3.021 is less than 3.12
Hence the probability of winning of Washington capitals is more than the Cleveland Cavaliers.
So Washington capitals are more likely to win their respective Championship.
#
🤐🤐
The statistics of small numbers and the very limited number of goals in a hockey game lead to NHL games being very random. All it takes is one more chance goal to put the Capitals way ahead of the Knights' average. More mathematically speaking, since the sample size of scoring events per game is so low (~4 for hockey and ~100 for basketball), the spread of scores is much broader in hockey games, and it's harder for real differences in ability to manifest above the randomly expected noise. So the underdog Capitals have a much greater chance of winning based only on the points/goals statistics than the underdog Cavaliers.
Biased coins
I loved Michael's analogy of the biased coins, so I'll expand on it a bit to show that the answer doesn't really depend as much as you'd think on how behind each underdog is in points per game. Note in this model we're assuming there are a limited number of scoring opportunities in a game, and the chance either team scores is represented by their relative "point per game" statistic.
As it stands, the Capitals are outscored by about 4 . 5 % while Cavaliers are outscored by 8 % . Let's make life even harder for the Capitals and say the Knights averaged 3.37 points per game. That would make the Capitals outscored by the exact same 8 % that the Cavaliers get outscored by.
Bringing in the biased coin: You have an unfair coin that has an 8 % higher chance of coming up tails than heads. So P ( heads ) = 0 . 4 8 and P ( tails ) = 0 . 5 2 . In which scenario would you rather bet on heads, the underdog result? Best of 5 flips of the coin, or best of 100 flips?
Of course you'd rather bet on best of 5 flips. Intuitively we could expect to beat the odds a couple times, but not over many many events.
Distributions
Here's the expected distribution for the number of heads flipped out of 5 for our biased coin (it's the Binomial Distribution ):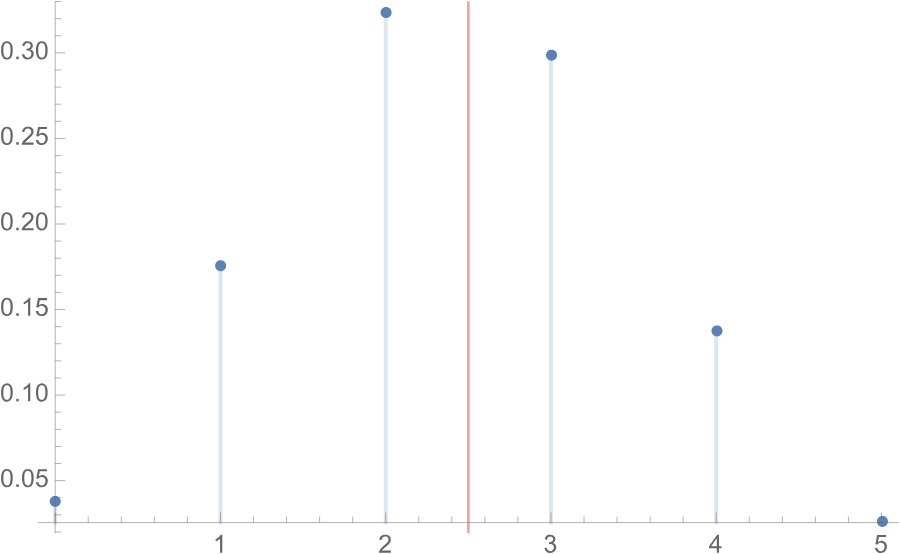 The odds of heads winning here is about
4
6
%
.
The odds of heads winning here is about
4
6
%
.
Now the distribution of expected heads out of 100 flips: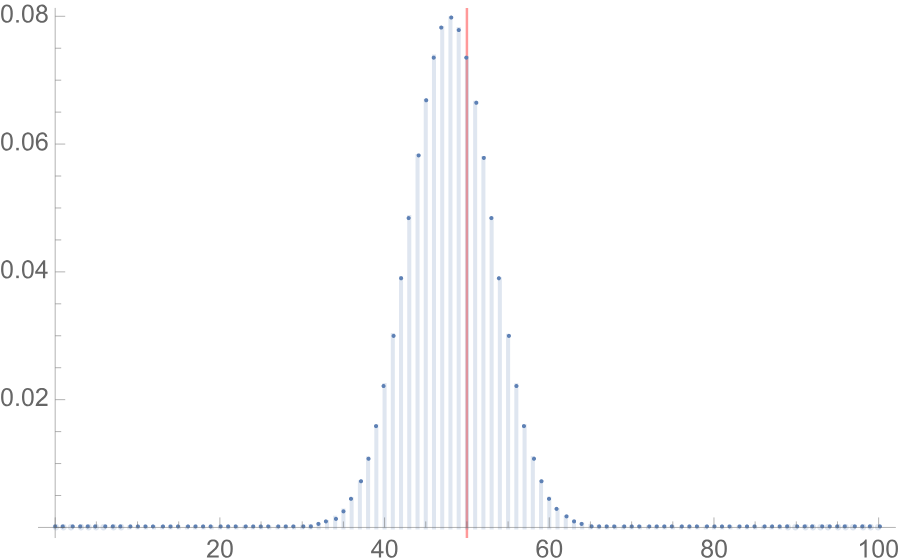 The odds of heads winning here is about
3
0
%
.
The odds of heads winning here is about
3
0
%
.
For 1000 flips, the chance of heads coming up ahead is less than 1 0 % .
When would the Stanley Cup be a sure thing?
Because of the low number of scoring events per game, hockey games are determined a lot more by randomness than by skill differences. Vox had a fun Youtube video about this last year ( Vox video ).
How much higher performing would a hockey team need to be (in this one metric, points per game) to make a hockey game as predictable as the Cavaliers Warriors game? Well, if we use the biased coin model above with an 8 % advantage to model a basketball game, 100 scoring events means the underdog will only win about 3 0 % of the time. With only 5 scoring events, the advantage would need to be 5 6 % to have the same underdog win rate, like if the Knights outscored the Capitals 4.5 points per game to 3.1.
Of course, this is a super simplistic view of both games. There is a lot more to it than points per games, including most notably each team's defensive performance. But the point that the low sample size of scoring events in hockey makes the game a bit less predictable based on prior performance remains.