A Golden Question

Algebra Level 2

$\large 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ldots}}}$ Find value of the expression above.

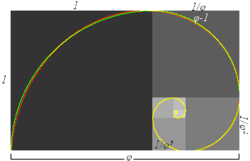
Image Credit: Wikimedia Golden Ratio by FakeRealLogSpiral

\frac{1+\sqrt{7}}{2}

\frac{1-\sqrt{5}}{2}

\frac{1-\sqrt{7}}{2}

\frac{1+\sqrt{5}}{2}

8 solutions

Shubhendra Singh
Feb 26, 2015

If $1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+ \ldots}}}=a$

Then $a = 1 + \dfrac{1}{a}$

$\Rightarrow a^{2}=a+1$

$\Rightarrow a^{2}-a-1=0$

$a=\dfrac{1+\sqrt{1^{2}-4(-1)(1)}}{2}$

So $\large \large a=\dfrac{1+\sqrt{5}}{2}$

Note:- $a\neq \dfrac{1-\sqrt{5}}{2}$ because $a$ can't be negative

Golden Ratio

Ñ Prâvéëñ Çhãñdhär - 6 years, 3 months ago

You might also want to clarify that we take the positive solution for the root because the original question clearly shows something greater than 0,

Daniel Ellesar - 6 years, 3 months ago

Consider the following function:

$f(n)=n+\frac{n}{f(n)}$

This represents the continued fraction function and for $n=1$ , we have the given problem. If you find the following limit: $\displaystyle \lim_{n\to 1} f(n)$ , you'll find that it is positive. So, the negative solution obtained is an extraneous solution and is to be rejected. Only the positive solution is the possible solution. This needn't be mentioned in the problem.

Moreover, if you think logically, the value of the expression is clearly $\gt 1$ and hence cannot be negative.

Prasun Biswas - 6 years, 3 months ago

I didn't mean that it should be mentioned in the problem, but it should be mentioned in the solution. The problem is fine, I just thought that this point wasn't immediately obvious from the solution given. Your explanation of it there is absolutely right.

Daniel Ellesar - 6 years, 3 months ago

I don't know that I agree with this being so cut and dry. Plugging in the negative number works consistently (which can be seen simply by plugging to your equation), so to discard it without giving a very, very good reason as to why isn't reasonable.

Also, I'd argue that the value of the expression is not clearly greater than one. That makes the assumption that the rest of the term is also positive. It seems rather circular to me: the expression is positive because its inverse is positive. Substitute in "negative" and the statement still holds. In addition, The only case I know of in which we can neglect the negative value is when it results in something like a division by zero.

You stated that the limit as n approaches 1 is positive. I'd like to see a proof of that, or at least an informal explanation of how you came to that conclusion.

Jacob Luciani - 6 years, 3 months ago

@Jacob Luciani – We can simply calculate the successive convergents of the continued fraction to conclude our answer too. Since I'm too lazy to calculate them manually, I used W|A. This is the link. Check the convergents section. As you can see, the values converge towards $\phi$ . But let's prove that. You can see there that the $k^{\textrm{th}}$ convergent $(a_k)$ is given by,

$a_k=\frac{F_{k+2}}{F_{k+1}} \\ \implies \lim_{k\to \infty} a_k = \lim_{k\to \infty} \frac{F_{k+2}}{F_{k+1}}~,$

where $F_k$ is the $k^{\textrm{th}}$ term of the Fibonacci sequence with $F_0=0,F_1=F_2=1$ . Use the closed form of $F_n$ to expand out the limit. The closed form is given by solving the linear recurrence of the Fibonacci sequence and is,

$F_n=\frac{\phi^n-\phi^{-n}}{\sqrt{5}}$

In the limit, $k\to \infty\implies \phi^{-(k+m)}\to 0~\textrm{for any non-negative integer } m$

The limit turns out as follows,

$\lim_{k\to \infty} a_k = \lim_{k\to \infty} \frac{\phi^{k+2}}{\phi^{k+1}}=\boxed{\phi}$

Since $\phi$ is the positive golden ratio, the continued fraction converges towards $\phi$

Prasun Biswas - 6 years, 3 months ago

yes..you're right

Saaket Sharma - 6 years, 3 months ago

i thought of taking the denominator's continuous part as a...i.e my expression would be like...a=1+(1/(1+a))......then i got my answer as root 2........is my assumption is wrong??

Shravani Mamidala - 6 years, 3 months ago

The substitution you made is wrong because of the following: $a=1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+ \ldots}}}\neq \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+ \ldots}}}$

Why is that? Why aren't the MHS and RHS equal? Because the RHS is $1$ less than the MHS and so the RHS is $(a-1)$ , not $a$ . Try to solve it again by keeping $(a-1)$ instead of $a$ in RHS of the equation you formed. That is to say, solve the following equation:

$a=1+\frac{1}{1+(a-1)}$

The answer comes out the same and it is $\dfrac{1+\sqrt{5}}{2}=\phi$

Prasun Biswas - 6 years, 3 months ago

he is right it is a = 1 + 1/a because the values below are the one that was being substituted..

Ojna Eugitaraba - 6 years, 3 months ago

@Ojna Eugitaraba – because if u will evaluate 1 + (a - 1) you will come up with a 1 + (a - 1) = a

Ojna Eugitaraba - 6 years, 3 months ago

@Ojna Eugitaraba – I know that! I was just explaining @Shravani Mamidala the mistake that he/she made.

Prasun Biswas - 6 years, 3 months ago

@Prasun Biswas – okk...thanks for your reply..it really helped me...thank you all @Ojna Eugitaraba @Prasun Biswas

Shravani Mamidala - 6 years, 2 months ago

Shravani, your assumption is right. But solution of the quadratic eqn is wrong. solution of a=1+(1/1+a) is not 2.

Bakul Majumder - 6 years, 2 months ago

Good solution...... easy way.

Anik Saha - 4 years, 4 months ago

Great awesome method!

Yoogottam Khandelwal - 6 years ago

Manish Bhargao
Mar 4, 2015

This is called as magic number and has value $1.618\quad$

Also named as the Golden ratio..............

A Former Brilliant Member - 6 years, 3 months ago

Er... It's not necessarily magic, although we do seem to like things proportioned by it. What is further, $\frac{1+\sqrt{5}}{2}$ is not equal to $1.618$ in the same way that $2.2$ is not equal to $2$ or that $8000006000 - 8000000000$ is not equal to $8000000000 - 8000000000$ .

WWT Manahan - 6 years, 1 month ago

Savira Utami
Mar 8, 2015

if a = 1 + 1/a so a^2 = a + 1 use a = (-b±√(b^2-4ac))/2a so a = 1 + √5 / 2 we choose positive because a can't be negative

Yoogottam Khandelwal
Jun 14, 2015

first i thought of guessing it..then i used the same method as Shubhendra did

Wwt Manahan
May 15, 2015

If $x = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\cdots}}}}$ , then we can say that $x$ is $1$ plus $1$ divided by all of that all over again--i.e.: $x = 1 + \frac{1}{x}$ Now multiply both sides by $x$ : $x^2 = x + 1$ Now subtract $x + 1$ from both sides: $x^2 - x - 1 = 0$ Now use the quadratic formula: $x = \frac{1\pm\sqrt{(-1)^2 - (4 \cdot 1 \cdot -1)}}{2 \cdot 1}$ Simplify some: $x = \frac{1\pm\sqrt{1 - (-4)}}{2}$ $x = \frac{1\pm\sqrt{1 + 4}}{2}$ $x = \frac{1\pm\sqrt{5}}{2}$ So $x$ is either $\frac{1 + \sqrt{5}}{2}$ or $\frac{1 - \sqrt{5}}{2}$ . Finding which of these is true is tricky. I resorted to just iterating the fraction further and further to see upon which value it converges--but you can't always do that because fractal fractions (as Vi Hart calls them) don't always converge.

Ka Kei Yeung
Mar 8, 2015

This is another way of writing the Golden Ratio.

Anna Anant
Mar 5, 2015

(1+√5)/2 is the answer

suppose x= 1+1/(1+1/(1+1/......)) then x = 1+1/x so x^2-x-1=0 so

x =(1-√5)/2 x =(1+√5)/2 but answer can't be nagative so 1+√5)/2 is the answer

Gamal Sultan
Mar 5, 2015

Let the given expression be denoted by X

Then

X = 1 + 1/X

X^2 - X - 1 = 0

Then

X = (1 + square root of 5)/2

A Golden Question

Image Credit: Wikimedia Golden Ratio by FakeRealLogSpiral

8 solutions

0 pending reports