So Many Nested Roots!
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 2 2 0 2 + 2 2 1 2 + 2 2 2 2 + 2 2 3 2 + 2 2 4 2 ⋯ = x y 1 1 + 1 3 + 2 1 5 + 3 1 7 + 4 1 9 + 5 ⋯ = x + y + a
If the system of equations above holds true for positive real numbers x , y and a , with y being a prime number, find the value of
3 a 3 a 3 a 3 a ⋯ .
Try another problem on my set! Let's Practice
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I was expecting that you could give a practical solution for the first equation.. I can't understand the explanation from the website that you've given there.
Log in to reply
Coz, i'm wondering, is it true that n n 0 n + n n 1 n + n n 2 n + n n 3 n + n n 4 n ⋯ = n
For n is a positive real integer..?
Log in to reply
I don't think so. If it works, I think the Wolfram MathWorld reference would have included it. The reference is quite thorough. It works for n = 1 and n = 2 . But I numerically check for n = 3 it diverges. The n = 2 is a special case of the equation below putting q = 2 1 , n = 2 , x = 1 and k = − 1 . You can try with different q to see.
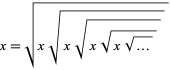
Log in to reply
@Chew-Seong Cheong – I am sorry for bothering you. But for me, I can't see it clearly, becoz it's a bit blur and I have a problem with my eyes.. Can you help me?
Log in to reply
@Fidel Simanjuntak – You mean you can't see the formula I posted? It is very long and complicated. Perhaps you can ask people around to jot it down for you.
Log in to reply
@Chew-Seong Cheong – Yeah, it's very long and complicated. Moreover, it's a bit blur..
@Fidel Simanjuntak
–
Sending you an enlarged image. I hope that it works.

From the reference on nested radical (eqn. 18) , we have:
2 2 0 2 + 2 2 1 2 + 2 2 2 2 + 2 2 3 2 + 2 2 4 2 + ⋯ = 2
⟹ x = 1 and y = 2 .
Using Ramanujan's formula (eqn. 26) below:
x + y + a = y x + ( a + y ) 2 + x y ( x + a ) + ( a + y ) 2 + ( x + a ) y ( x + 2 a ) + ( a + y ) 2 + ( x + 2 a ) ⋯
Putting x = 1 , y = 2 and a = 1 :
1 + 2 + 1 = 2 + ( 1 + 2 ) 2 + 2 ( 1 + 1 ) + ( 1 + 2 ) 2 + ( 1 + 1 ) 2 ( 1 + 2 ) + ( 1 + 2 ) 2 + ( 1 + 2 ) ⋯ = 1 1 + 1 3 + 2 1 5 + 3 1 7 + 4 1 9 + 5 ⋯
⟹ a = 1 . Therefore, 3 a 3 a 3 a 3 a 3 ⋯ = 3 1 3 1 3 1 3 1 3 ⋯ = 1