Remembering Last Year
2 0 = 1 5
Is it possible to make the equation true by inserting the appropriate operations? Any operations and functions can be used.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
274 solutions
This one was mine too :)
Simple and beautiful solution!
what is the exponent sign?
Log in to reply
In computer coding, I usually use the carrot sign "^" for exponents.
Log in to reply
I cant really say you are wrong!
That's what I was thinking!
It said, by adding functions.. Not moving the numbers tho
Can be also be the solution.
same answer
Yep that was my solution
mmm this, to me, is a dodgy solution, because you aren't "inserting" -operations-, as the question asks you to. a technicality, true, but still...
2^0. that is an example of the exponent sign for any who don't know the symbol.
Is ^ considered an operation?
0 0 (20) = ( 15)
"exponent" is NOT a sign.
I got that too
2^2 +0 = -1+5
2+0 = 1x.5
20% = 1/5 Well, not a function, but if you would allow %.
Log in to reply
.20 = 1/5 .....................................
2.0=1/.5 ?
beautiful..........
My answer was this
2 to the power of 0 is 0, 1 to the power of 5 is 1 so that doesn't work cos 0=1 is wrong...
Log in to reply
It is a mathematical certitude that any number 'to the power of' (indicies) 0 equals 1. eg. 3(pow)0=1 , 17(pow)0=1
https://www.google.com.au/url?sa=t&source=web&rct=j&url=https://answers.yahoo.com/question/index%3Fqid%3D20100514234210AANn2op&ved=0ahUKEwiq-8HT35LQAhUCJZQKHfLMDwMQFgheMAY&usg=AFQjCNEoxxK-ts933xn giH7p-v4r a7ug
Dan - ouch. 2^0=1
There is no logical meaning for inserting the exponential sign in between a numbers. The actual solution goes like this:
(2^0)+0=(1^0)*(5^0)
Log in to reply
I'm sure this isn't legal. You've inserted two numbers. You may only use 2 and 0 on the left and 1 and 5 on the right. You may only use any function that incorporate the given numbers (once each).
You negated your own argument IMHO
That makes no sense, if we cannot insert 2^0 or 2 (x^y) 0 then we also cannot insert +, - , / or * . We were allowed to use operation and functions! Plus - you added numbers that weren’t there to begin with?
2 0 = 1 5 ( 2 + 0 ! ) ! = 1 + 5
BONUS: Try this one 2 = 0 1 5
Log in to reply
Similar to my solution below 2 = 0 + − 1 + 5
Log in to reply
then the answers will be +2 & -2
Log in to reply
@Amin Khan – The radical sign is read "the principle square root" which is always positive. Kay is correct.
Log in to reply
@Leslie Koller – sqrt (4)=+2, -2 then -2 is not equal to 2
Log in to reply
@Amin Khan – But sqrt(4) IS NOT +-2, the sign when written is called the Principle Square root, which is ALWAYS positive. Take the quadratic formula...x = -b +- sqrt... If sqrt meant + or minus we would write only the plus part of the discriminant.
@Amin Khan – No. Although 2 2 = ( − 2 ) 2 = 4 , the value of 4 = 2 and not − 2 , the latter of which represents − 4
No.... The = sign should be between 0 and 1.
Log in to reply
@Bhupendra Jangir – If you notice the boldface In response to Rishabh Cool , I am directly answer his question when equal sign is between 2 and 0. Indeed, for the original question, my solution is separately posted below.
2 = 0! + 1^5
0 - 1 + 5 = 2square
Log in to reply
Good one!!
But adding a square or a cube is like adding a number.
Log in to reply
@Shubhang Mundra – If adding a square(2) or cube(3) is like adding a number, then don't you think that adding a square root(1/2) is also as equal to adding a number, which by means implies that all calculations using the roots go in vain, where it results an end to this king of game playing.
So adding cube or square is as equal to adding a root thus Rishabh is correct...
It could be like this 2=√(0-1+5)
2 = 0! + 1^5
2 = ⌊ 0 ! + 1 5 ⌋
2^(-1)=0.1*5
How to do it
Log in to reply
2 = 0 + 1 + ⌊ ln 5 ⌋
Log in to reply
@Rishabh Jain – Are you using the greatest integer function in this? It just looks like brackets
@Rishabh Jain – Wow,nice Rishabh!I see you're posting fantastic solutions these days!BTW how old are you?
Log in to reply
@Rohit Udaiwal – J = 2 1 − i = 1 ∑ 1 6 i 2 + 3 i + 2 1 . J can be represented as m/n(m,n are coprime), then my age is |m-n|......
Log in to reply
@Rishabh Jain – It's 17 right?
@Rishabh Jain – A very good solution.
Log in to reply
@Shubhang Mundra – What's your actual name in school, and in which class you are studying,can you plz tell me
Log in to reply
@Shubhang Mundra – Rishabh!! Currently not in mps but I am a passout of mps. Currently studying in 12 class.
@Rishabh Jain – But ln ( ⋅ ) is a function, not an operator
Log in to reply
@Jason Simmons – Taking natural log of a number can also be a operation....
2 = 1 + 5^0
this is perfect
Wow, nice thinking to use factorials.
I thought about power. But your solution, I really love it.
Very Nice thinking! Great!
I did it in the same way xD
This was my solution!
Vert clever
Exactly! nice !
I also thought similar. 20%=1/5
% and : are not operations or functions
Log in to reply
Sure they are. % means divide by 100. The symbol : means divide by, of course. 1:5 = 1/5.
Nice and Simple.. :-)
That's what I thought :)
Pretty sure 1:5 =1/6
Log in to reply
That's probably not something you should admit.
Depends which side of the ratio you mean, but yes it is dealing with sixths
To make it more complex we can do this also 2=Square root of (I(-1+5)I)
Among other things, 2^0 = 1^5
wow, I was way too complex 2^2 + e^0 = log(1) + 5
Is modulo allowed? 2^0 = 1%5
I did this .2 + 0 = 1/5
My terms is 2 + 0 = − 1 + 5
Wow, that's clever! I like it! :)
Nice, that was my solution also.
One for the logicians 2 > 0 = 1 < 5
This was also my answer
? I don't understand, please explain if you can.
Best answer yet!
My favourite solution
So you're saying 0 = 1?
True == True
Notice that to say Yes, one has to just make perform the operations desired, but to say no, one has to prove it.
Since any operations is not sufficiently defined, such a statement cannot be proven.
Hence, it must be yes
My thoughts exactly. Any question that has a 'yes/no' answer on here will have to be 'yes', otherwise the correct answer would be chosen from a selection of four or more possible answers.
:O Yeah maybe they should change that. However, idk if they should, because some of us could know the correct solution and not know how to write it. I used scientific notation but I didn't know EXACTLY how to write mine XD.
In fact since the say "any function" can be used, you could also simply just define functions f and g such that f(2) = g(6), and then argue that therefore f(2+0) = g(1+5).
Basic logic. Perfect.
Makes sense!
Is .20 a correct way of writing a decimal fraction - shouldn't it have to have a zero before the decimal point? However 20% = 1/5
It is correct. I can't stop laughing. XD
A new one: 2 × 0 = ⌊ 5 1 ⌋
He's using the greatest integer function here for the 1/5. The greatest integer that is less than 1/5 is indeed 0, so this solution is correct.
2x0 is 0, so this is wrong
Log in to reply
It's unclear why you think that because 2x0 is 0, this solution is wrong. Regardless, it's not.
2 + 0 = ϕ ( 1 ) − μ ( 5 ) 2 ! + 0 = Γ ( − 1 + ϕ ( 5 ) ) − μ ( 2 ) + 0 = μ ( 1 ) μ ( 5 ) ϕ ( 2 ) − 0 = ϕ ( 1 ) 5
For those who are interested refer to the wikis
2^2+0=-1+5
Umm isnt this a little too complicated? There's always 2^0 = 1^5...
This is the one I first thought of.
Did it the same...
You cannot just add extra digits. Where did the other 2 come from?
Yes. Bcause of this
2^0=1^5
2 × 0 = cos ( arcsin ( 1 ) ) × 5
Nice one! I like how you used trig!(you can use hyperbolic functions as well)!
2 0 = 1 5 ==> 2 0 % = 1 ÷ 5 ==> 20% = 1/5
2 0 = 1 5 ?
Doesn't this count?
I think this one is actually really nice
Here's an obvious one - 2 0 = 1 5
That is what i came up with
Would it be allowed to insert a decimal? Then you could do:
.20=1/5
Similar to this but: 2^2 +0 = -1+5.
Since 0! = 1, 2-0!=1^5 is valid.
1 divided by 0.5 is 2 so: 2+0=1÷.5
2 is 0 = 1 is 5 -> false = false
There is only one 2 in the problem, but you put two in your solution.
It says any function or operation can be used. Instead of thinking of a solution involving common operations I can just define a function that returns the same number for any arbitrary operands.
Nope. First of all, you have to only use the digits given. Second of all, 0^0 is not defined. It isn't 1.
2^0=1^5
2 power 0=1
1 power 5=1
If we can use expopents: 2^0=1^5
I agree with the exponent solution
f ( 2 0 ) = g ( 1 5 ) where f=g=0
I was thinking 2 times 0 and 1 mod 5
Yes multiply both sides by zero both becomes equal
.20=1/5 using the decimal point before the 2 and the divide between the 1 and 5
(2^2)+0!=1*5 This is a bizarre solution, but it works.
2^0 = 1 1^5 = 1
1=1
2 0 ( b a s e 1 0 ) = 1 5 ( b a s e 1 5 )
Raising ANY number in the power of 0 does ALWAYS give 1. So 2 in the power of 0 = 1.
Raising 1 in ANY power shall FOREVER repeatedly give 1. So, 1 in the power of 5 = 1 1 1 1 1 = 1.
And THUS, 2 in the power of 0 = 1 in the power of 5 = 1. :-))
20-5=15 He said ANY operations☺️
I used: 2 ∗ 0 = 1 − ( 5 0 )
may be against the rules, but I was thinking...
( 2 + 0 ) 2 = ∣ ( 1 − 5 ) ∣
-2^2 + 1 - 5 Make two negative, square it.
2 to the 0 power = 1
1 modulo 5 = 1
Bit rusty on what constitutes an operation or function, but this is my guess. .20 = 1/5
2 x 0 = \arccos(1) x 5
No one is finding what is arguably the simplest way to solve this problem.
2*0 = /frac {1}{5}
I don’t know how to insert the greatest integer symbol around the fraction, but since the greatest integer to 1/5 is 0, this is correct.
d/dx(2)+d/dx(0)=d/dx(1)+d/dx(5)
2^0 = 1^5
since x^0 is always 1 so as 1^x is always 1 too.
20 >= 15 should be a valid solution to this puzzle. And if spaces cannot be removed then this should do: 2 - 0 >= 1 - 5
You could use the inequality operator to return true;
20 != 15
This works too
⌊ 2 + 0 ⌋ = ⌈ 5 1 ⌉
My solution was
2^2 + 0 = -1 + 5
It may have some flaws though since adding the 2 may be cheating
If percentage counts as an operation -- and I don't see why it wouldn't -- then this can be a fraction conversion sentence.
20% = 1/5
If an arithmetical operation consists of any function mapping a set of natural numbers to a natural number, then the function f(20) = 15, f(x) = x otherwise, is a solution. For another solution, define a function called 'predecessor' 'p' such that p(0) = 0 and p(n + 1) = n for any natural number n. Similarly, define f(0) = 0, f(1) = 0, f(2) = 0, f(3) = 0, f(4) = 0, f(n + 5) = n. So, f(20) = 15 and thus works as such a function.
putting a decimal pint before 2 and a dividing 1 by 5
.20 = 1/5
-(2²) + 0 = 1 - 5
ANY operations and functions, eh?
Well, then let say f ( 2 ) = 0 , g ( 0 ) = 0 , h ( 1 ) = 0 , and j ( 0 ) = 1 .
Then f ( 2 ) × g ( 2 ) = h ( 1 ) × j ( 5 )
I know this isn't the intent, but either say what you mean or mean what you say.
20% = 1/5 I know % isn’t a function. But as given, the numbers aren’t assigned values. Also works as: .20 =1/5
2^0=1^5 any number to the zero power is 1; 1 to the fifth power is 1
u(15)=u(20) where u is the unit step function
2^0 * 0^0=1^0 * 5^0
1* 1=1* 1
1 = 1
2^2+0=1-5 makes them both 4
2^2=4 1-5=-4 But you could do -(2^2)+0=1-5
.20=1/5 This shows a fraction and a percentage.
Make left side of equation to base ten and right side of equation to base fifteen
.20=1/5 by putting decimal on lhs and by diving 1 by 5 on rhs
2^2+0^2= -(1)^2 + 5
Thought basically this just means:
2^2 + 0 = -1 + 5
2^0 = 1^5 Both results simplify down to the number one.
By inserting a decimal on the left and a division sign on the right:
.20 = 1÷5
I used scientific notation to make 1= 100. then I divided it by 5 to make 20. dabs So satisfying!
2 = 0-1+5. I moved the = !
2x5=1+9 Played with multiples of 5and10
Or you could go unconventially and make it 20≠15
20%=1:5..... I think this will be the answer
Counting in a base 5 system.
One can use exponent and modulus operations. Like this: 2 0 = 1 mod 5
Put a decimal in front of the 2, make the right side into a fraction.
.20 = 1/5
Assuming we can use any base logarithm...
l o g 2 0 2 0 = l o g 1 5 1 5
1 = 1
"Any operations and functions can be used." I define the function f(x)=x-5
f(20) = 15
I'm not sure if this is used in mathamathics, but the mod function from CS is possible 2%0 = 1%5
Decimal 2 is 2/10. 1/5 = 2/10. Assumes that inserting a decimal is permissible .2+0=1/5
I think this one could be a solution: ( 2 + 0 ) 2 = ∣ 1 − 5 ∣
2x + 0 = x + 5
2x - x = 5 - 0
x = 5
then 2 . 5 + 0 = 5 + 5
10 = 10
By multiplying 2 and 0 in LHS and taking the step function of the fraction obtained by dividing 1 with 5 (0.2) in RHS, we get 0=0 i.e.,
2 * 0 = [ 1 / 5]
Using modular arithmetic i.e. 20 mod5 = 15 mod5 =0
2 (addition modulo 2) 0=1 (addition modulo 2) 5
Also works with multiplication modulo 5
20 ≠ 15 .... took the easy root just drew a line through the equal sign ... TADA
Haha i knew it could be done other ways and this might not even be allowed by the rules of the question .... but you gotta break a few eggs to make an omelette XD
2 + 0 = the square root of (-1+5)
2*0=1 * (((\frac{d}{dx})) 5)
That's mine too. 👍
2 x 0 = {1} x {5} where {.} is fractional part
Subtract 5 from 1, take absolute value, then square root. Subtract 2 from 0. 2=2 i.e. 2 + 0 = ∣ 1 − 5 ∣
20=15 Add an operation so that 20 becomes 15 Eg 20 - 5 = 15 Or 3/4 of 20= 15 Etc
2+0=mod(sqrt(mod(1-5)))
Another solution: 2 0 ≠ 1 5
Sooooo if you use (.)2 0 = 1 divided (/) into 5 One fifth is one fifth
Tadaaaa Thank you
20 >= 15
This would appear to be the simplest solution to the problem.
The equation can be made true by simply inserting a 'Not equal' symbol. B-)
I thought of − 1 + 5 on the RHS and 2+0 on the LHS
by adding the power operator in both sides 2^0 = 1^5 = 1
Add a slash across the equal sign to make it a not equal sign. The statement then becomes true.
Simply put "^" sign bet no. 2^0=1^5
Totally simple and straightforward. 2^0 = 1 = 1^5
I figured it out this way (2^2)+0 = -1+5
RHS-2 raised to power 0 is equal 1 & LHS 1raised to power 5 is also 1 so LHS =RHS
It could be 2-0! = 1^5
2*0=1 Integral division 5 ? It would work in C.
The point can be seen as an operator as well. .20 = 1 / 5
.20 = 1/5. Add a decimal point before 2 and divide 1 by 5
Seems pretty simple to me the two answers don't equal each other hence: 2 0 ≠ 1 5
I thought about putting a decimal place before the 2, and a division sign between 1 and 5.
Is adding a decimal point legal? 2+0 = 1 / .5
20 !=15
Or
2.0 = {1}.5
2 ^ 0 = 1 ^ 5.......
SO SIMPLE
.20 = 1/5, veery similar to the solutions using %
2 > 0 = 1 < 5 or 2 < 0 = 1 > 5
2 0 = 1 5 or if you prefer an operator to be inserted, 2 0 ¬ = 1 5
Here is my solution
.20 = 1/5
2^0 = 1
1^5 = 1
So 2^0 = 1^5 = 1
If any operation may be used, then it may be defined too. There are ℵ 0 ℵ 0 2 = ℵ 0 ℵ 0 = 2 ℵ 0 = ∣ R ∣ binary operations defined in Z and the same number of them in which a ? b = c ? d for some choice of integers a , b , c , d . So we can define ⊗ such that 2 ⊗ 0 = 1 ⊗ 5 = 3 3 3 3 3 and a ⊗ b = 0 in any other case, and we get a solution.
Here is another solution : 2+0=1+sgn(5)
Utilizzare l'esponente 2^0=1^5
So I have three ways.
The first one is making the second number the exponent of the first. So 2 0 = 1 5 which is 1 = 1
The second one involves factorials. (2 + 0!)! = 1 + 5 which is 3! = 6
The third one is rather extreme and it's actually the first one I used :3
2 + 0 = | 1 - ceiling ( 5 ) |
2 + 0 = | 1 - 3|
2 = |-2|
Havent seen this solution yet: 20%=1/5
Can this be : 2^2 - 0 = -1+5
0.20=1/5 If you devide 1 over 5 gives you 0.20
I was thinking about integration and trigonometry jajaja but... 2 2 + 0 = ( − 1 ) + 5 simple is always better.
Just add a decimal in front of the 20, then a division sign between 1 & 5. Tada! .20=1/5
Make the first a decimal and add a division sign in the second.
.20=1÷5
2x0=1 div 5 Is this acceptable lol
(2!+0!)!=6 & 1+5=6 So, it becomes (2!+0!)!=(1+5)
Make the second number on each side an exponent
Thus, you get 2^0 =1, and 1^5=1
Both sides equal 1, so it is possible to make both sides equal to each other.
20^(Log15base20)=15
2+0 = squareroot(mod(1-5))
It seems a lot of people think alike. There are only a handful of folks who didn't do exponents.
Any function is allowed? Define f(x) such that f(0) = 1 + f(5). Done.
if you see any question starting with ( is it possible ) .. The answer is yes
yah we should equate by considering the power.
Here is a slightly underhanded approach, in addition to the ways given below.
In Java, if we declare the variables a , b , c , and d of type int and initialize them to 2 , 0 , 1 , and 5 respectively, then 2 × 0 = 1 / 5 .
But you have to use floor function
Log in to reply
Integer division is automatically floored. If you run the following program in Java, it will print 0 .
public class Test{public static void main(String[]args){int a,b,c,d,e;a=2;b=0;c=1;d=5;e=a*b-c/d;System.out.print(e);}}
That is true in several languages as well. Internet hi-five from fellow coder.
d x d 2 d x + d x d 0 d x = d x d 1 d x + d x d 5 d x
ϕ ( 2 0 ) = ϕ ( 1 5 )
2 − 0 = − 1 + 5
2 − 0 = − 1 . 5
⌊ 2 0 ⌋ = ⌈ 1 5 ⌉
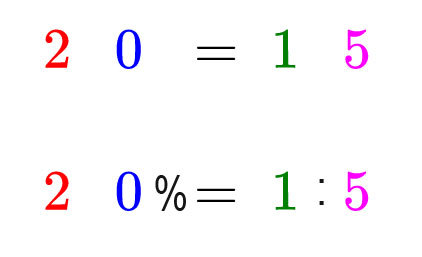
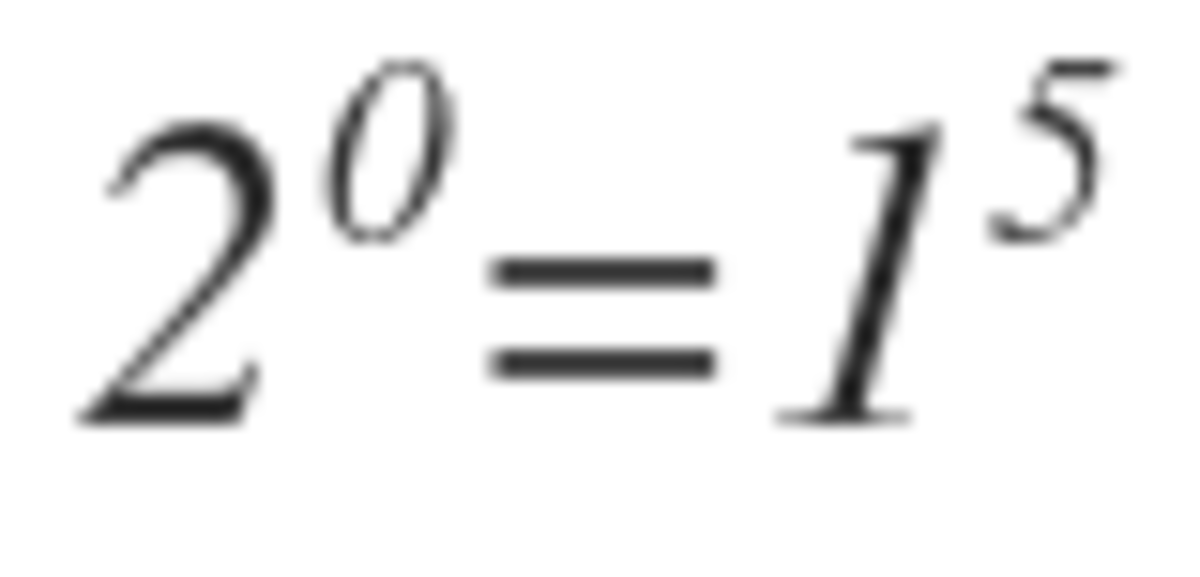
By putting the exponent sign between the two numbers
i.e.
2 0 = 1 5