NMTC Inter Level Problem 10

Geometry Level 2

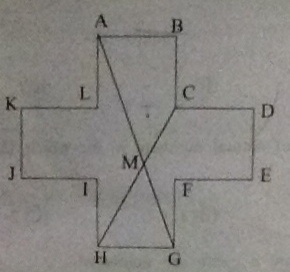Consider the figure $ABCDEFGHIJKL$ as shown. Each side is of length $4$ and the angle between any two consecutive sides is a right angle. $AG$ and $CH$ intersect at $M$ . The area of the quadrilateral $ABCM$ is $\text{\_\_\_\_\_\_\_\_\_\_}.$

\frac{44}{3}

\frac{88}{5}

\frac{62}{3}

\frac{77}{9}

3 solutions

Brian Charlesworth
Aug 28, 2014

First, situate the shape on an $xy$ -grid so that point $H$ is at the origin and side $HG$ lies along the positive branch of the $x$ -axis.

Then $HC$ lies on the line $y = 2x$ and $AG$ lies along the line $y = -3x + 12$ . These two lines intersect when

$2x = -3x + 12 \Longrightarrow x = \dfrac{12}{5}, y = \dfrac{24}{5}$ .

Now the area of the quadrilateral $ABCM$ is equal to

(area $ABGH$ ) - (area $\Delta AHM$ ) - (area $\Delta HMG$ ) - (area $\Delta CMG$ ))

$= 4*12 - (\frac{1}{2})(12*\frac{12}{5}) - (\frac{1}{2})(4*\frac{24}{5}) -(\frac{1}{2})(8*\frac{8}{5}) = 48 - \frac{152}{5} = \boxed{\frac{88}{5}}$ .

There's a number of typos, fix them..

Here's the fixed version: $4\cdot 12 - \frac{1}{2}\left( 12\cdot \frac{12}{5} \right)-\frac{1}{2}\left( 4\cdot \frac{24}{5} \right)-\frac{1}{2}\left( 8\cdot \frac{8}{5} \right)$

mathh mathh - 6 years, 9 months ago

If you look at my bracketing, I took the common factor of $\frac{1}{2}$ outside and then bracketed the remaining terms, so there are in fact no typos. If you'd prefer it your way that's fine, I'll make the edits, but I just want to make the point that my solution is correct as it is now.

Brian Charlesworth - 6 years, 9 months ago

oh, sorry :( didn't notice the brackets.

BTW, I wrote a C++ code for your problem All tapped out .... and it looks like $\frac{95}{68}$ is the answer, unless I did something wrong, in which case sorry again. I haven't seen your solution yet by the way.

The time it takes for the $n_1$ 'th, $n_2$ 'th and the $n_3$ 'th tap to fill the pool together is

$\frac{1}{\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}}=\frac{n_1n_2n_3}{n_1n_2+n_2n_3+n_3n_1}$

And here's the code that calculates the expected time (the last number of the output is the answer. It is not exactly $\frac{95}{68}$ but quite extremely close to it):

float i,m,n;
float newsum=0;
    for (i=1;i<=10;i++)
        for (m=i+1;m<=10;m++)
            for (n=m+1;n<=10;n++) {
                newsum=newsum+(m*n*i)/(i*m+m*n+n*i);
                cout << newsum << endl; }
    cout << newsum/120.0;
    return 0;

mathh mathh - 6 years, 9 months ago

@Mathh Mathh – No problem. I ended up making the edits you suggested; it does read more clearly your way. :)

As for my other problem, your approach is excellent. I made a dumb mistake in assuming that $E[\dfrac{1}{X}] = \dfrac{1}{E[X]}$ , when in general this is not true, (and is definitely not true in this case). I am going to ask the moderator to change the answer to $95 - 68 = 27$ , or possibly 1.397, give you credit for coming up with the correct answer and then delete my solution. Hopefully that will get rid of the dreaded "Action required" box.

Brian Charlesworth - 6 years, 9 months ago

@Brian Charlesworth – Make the answer approximate ( $1.397$ ), since it appears that it is not $\frac{95}{68}$ (it was just my guess and it looks like it is not right by about $\approx 0.0000133$ ). It is

$1.397045516967773348682158029987476766109466552734375...$

Or you can try calculating the actual value.

mathh mathh - 6 years, 9 months ago

@Mathh Mathh – Great. I've suggested changing the answer to $1.397$ , (along with suggesting the appropriate changes to the wording of the question so that there is no mention of $\frac{a}{b}$ ), so hopefully the moderator will accept those changes.

Brian Charlesworth - 6 years, 9 months ago

Dagh Nielsen
Dec 3, 2016

The computations are a bit easier if we make the side lengths 1 and then multiply our result by $4^2=16$ afterwards.

We can calculate the area of $\square ABCM$ as

$\square ABGH - \triangle AGH - \triangle BGH + \triangle MGH$ (We take away two triangles and add back the double counted common part.)

We can calculate the area of $\triangle MGH$ by finding the height from $M$ . Since the "slopes" of the sides are 2 and 3, the height happens after $3/5$ of the base, which multiplied by the left slope, 2, gives a height of 6/5.

All in all:

$\square ABCM=\square ABGH - \triangle AGH - \triangle BGH + \triangle MGH=3-1.5-1+\frac{6}{5} \cdot \frac{1}{2}=\frac{11}{10}$

and multiplied by $4^2=16$ we get $\boxed{\frac{88}{5}}$

Daniel Bachelis
Nov 22, 2016

I did a simpler solution.

find the height of $M$ from $HG$ .

$HG = 4$

Splitting $HG$ into two pieces $a$ and $b$

$3a = 2b$ ,

$a + b = 4$ ,

$a = \frac{2}{3}b$ ,

$b = \frac{12}{5}$

$2b = \frac{24}{5}$

Extending $HC$ , it hits a point $P$ such that $ABP = 6$

$ABCM = APCM - BPC$

height of $APCM$ is $12 - \frac{24}{5} = \frac{36}{5}$

$ABCM = \frac{1}{2} 6*\frac{36}{5} - \frac{1}{2}2*4 = \frac{88}{5}$

NMTC Inter Level Problem 10

3 solutions

0 pending reports