No calculator allowed!
3 2 + 5 + 3 2 − 5
My calculator says that the above expression equals 1.
But is the answer correct? Or, is 1 just an approximation?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
That's amazing. I had no idea that a complicated expression like these would simplify to 1.
Your solution hinges on the assumption that the given expression is a real number. Why would that assumption be correct?
Log in to reply
Other than the square root (which is done directly on a positive number 5 in both cases so the result is real) all the operations are closed in the real numbers.
This solution takes advantage of the fact that the quadratic factor has a negative discriminant. But suppose it does not have a negative discriminant, then the expression will be multi-valued, right?
Log in to reply
The discriminant will never be non-negative, because the expression can only take on the value of one real number. I suppose there will be multiple values if we were working with even roots rather than odd roots, and we allowed complex solutions.
I don't think this solution is correct. I believe that the answer is that the given expression is complex, and hence the three given answers ("1", "less than 1", "bigger than 1") do not exhaust the possibilities. This is frustrating. For instance, in your solution you assume that the third root of -1 is equal to -1, but this is not correct. There are in fact 3 solutions, the other two are 0.5 +- i*Sqrt[3]/2. Which one is correct requires discussions of branch cuts, which I can't find in your solution. In fact, the trouble already starts with the given expression itself: 2-Sqrt[5] is negative, so somebody needs to tell us what branch cut to take to make sense of taking the third root of this.
Log in to reply
There aren't three solutions. The cube of a negative number is another negative number e.g. ( − 1 ) 3 = − 1 . So, the cube root of a negative number is still real, meaning that the expression cannot take on a non-real value.
@Steven Yuan - You're using what MathWorld calls the "school book" definition of the cube root of a negative number. Why are we supposed to presume, in an "advanced" forum like this, that math ends at the school book level? In fact, since roots are properly discussed in the complex plane, and the standard branch cut for roots runs along the negative real axis, the principal value of the cube root of a negative number always is complex. The fact that you happen to be able to make sense of the argument by staying within the reals doesn't by itself mean that this is therefore the way in which standard mathematics handles the problem. I suggest to have a look here: http://mathworld.wolfram.com/CubeRoot.html
Log in to reply
You are correct that, for negative values of x , there are three possible values for x 1 / 3 in complex numbers. However, it is implied in the problem statement that we are working entirely within the real domain, as the calculator gave a real number value for the expression and not a complex one. So, there is no error in the problem nor the solutions.
@Steven Yuan - "However, it is implied in the problem statement [...]" That's what I find so frustrating. What is or isn't implied is very much in the eye of the beholder. Are you sure all calculators give the same result? When I evaluate the formula in Mathematica, I get the "conventionally correct" answer 1.92705 + 0.535233 I. If I by hand swap the second term into -(Sqrt[5]-2)^(1/3), then I get 1. In other words, I have to second guess how "naive" any given pocket calculator deals with roots, or I might have to assume that every pocket calculator is as naive as the one I'm using. That is not mathematics. I believe the correct answer is that this expression is -- by the standard convention that modern mathematics uses -- a complex number, and that the answer choices are missing a "none of that" as the solution. The people of "Brilliant" have been a bit quick in assuming that the school book definition of math is just fine here. I don't like to be told I'm wrong, if the "intended correct" math answer would get me wrong at university, even if it gets me right in high school.
Log in to reply
If you think there's an error to the problem, post a report. I can't really address your concern myself, so I'd rather let the Brilliant staff handle it.
While you would be correct if the problem was asked about the general expression, it's being specifically asked if a calculator that provides a value of 1 is making an approximation or not. This doesn't require interpretation in terms of what the actual mechanics of the calculator are.
If the calculator was somehow attempting and failing to provide the principal value of the cube root there would be complex component to the number.
You are correct that Mathematica always gives the principal value of a root.
I can't seem to post a new solution to a last week's problem, so I'll just comment here. The expression is equivalent to the cube root of the cube of the golden ratio phi plus the cube root of the cube of 1 minus phi. So it evaluates simply to phi + 1 - phi = 1. Skip Richards
[This is not a complete solution. It is similar to Steven's.]
Let x = 3 2 + 5 , y = 3 2 − 5 . We get that x 3 + y 3 = 4 and x y = − 1 . Hence, show that x + y = 1 .
Yes, these are observations one could make to deduce the answer.
Solution 1
The problem immediately reminded me of a solution to a cubic equation: x 3 + p x + q = 0 ⟹ x = 3 − 2 1 q + 2 1 q 2 + 2 7 4 p 3 + 3 − 2 1 q − 2 1 q 2 + 2 7 4 p 3 . (This is the real solution if there exists only one.)
Matching this with the expression given here, − 2 1 q = 2 ∴ q = − 4 ; ( − 4 ) 2 + 2 7 4 p 3 = 2 2 ⋅ 5 ∴ p = 3 . Thus the expression is the only real solution of the equation x 3 + 3 x − 4 = 0 . Clearly, x = 1 is a real solution of this equation, so that the expression is indeed equal to 1.
Solution 2
Let a ± = 2 ± 5 . I don't like the look of roots inside roots, so I played around a bit to get rid of that. For instance, a + a − = ( 2 + 5 ) ( 2 − 5 ) = 4 − 5 = − 1 , 3 a + 3 a − = 3 a + a − = 3 − 1 = − 1 .
Suppose now that we have two numbers, x + and x − , for which this property is true and your calculator is right. { x + + x − = 1 x + x − = − 1 . They must be the solutions of x 2 − x − 1 = 0 , namely x ± = 2 1 ± 2 1 5 . Now use x 2 = x + 1 to evaluate the cube of either solution: x 3 = x ( x 2 ) = x ( x + 1 ) = x 2 + x = ( x + 1 ) + x = 2 x + 1 , so that x ± 3 = 2 ( 2 1 ± 2 1 5 ) + 1 = 2 ± 5 . We see that our x ± are precisely the 3 a ± , as we needed to show.
I quite like the second approach because it approaches the problem from a different angle. Unfortunately it turns out to be no simpler than the more obvious solution. I suspect it would work better in more complex problems.
The problem immediately reminded me of a solution to a cubic equation: x 3 + p x + q = 0 ⟹ x = 3 − 2 1 q + 2 1 q 2 + 2 7 4 p 3 + 3 − 2 1 q − 2 1 q 2 + 2 7 4 p 3 . (This is the real solution if there exists only one.)
But how do we know if there's only 1 real roots (and 2 non-real roots)? Or, put it another way: If the cubic equation has 3 real roots, then your "x= ..." will produce what kind of root? The smallest? The largest? The median root?
Log in to reply
In the case of three real roots, the discriminant (expression on the inner square roots) would be negative, so that x = 3 complex number + 3 complex number . At first it may seem baffling that this describes a real root, but it works! (The two complex numbers are complex conjugates, so the imaginary parts cancel when they are added.)
(The formula is still correct with three real roots, but practically useless. There are better and more interesting methods to find the roots; for instance, one involves drawing a circle centered at − 3 1 p , choosing three points at 1 2 0 ∘ intervals, in a direction determined by p and q , and projecting them onto the number line.)
Since in the problem at hand we were given a root of a positive number (5), x had to be the solution of a cubic equation with only one real root!
Log in to reply
... for instance, one involves drawing a circle centered at − 3 1 p , choosing three points at 1 2 0 ∘ intervals, in a direction determined by p and q , and projecting them onto the number line.)
I'm unfamiliar with this approach. Got a reference that I can look up to?
Log in to reply
@Pi Han Goh
–
I don't have a reference, but I can reconstruct the argument.
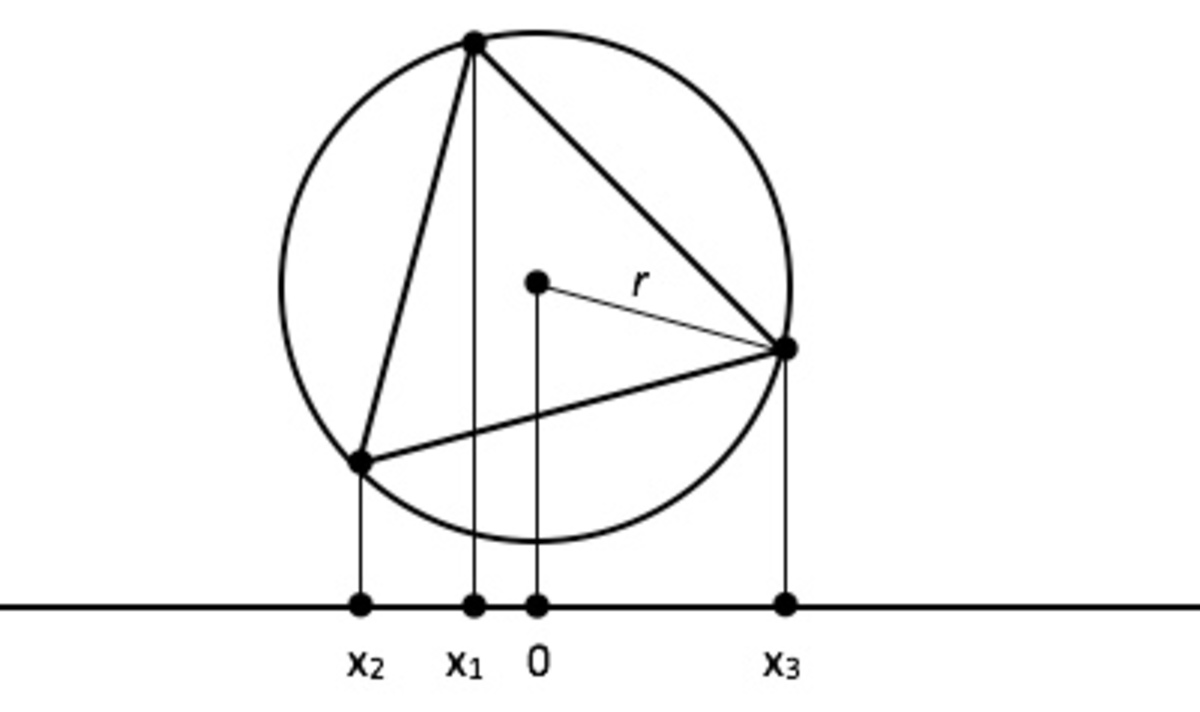 Consider a circle of radius
r
centered at 0 (contrary to what I stated before). Pick three points on that circle,
1
2
0
∘
apart from each other. Let
x
be the
x
coordinate of one of these points. Then
x
=
r
cos
θ
for a certain angle
θ
. Now
x
3
=
4
1
r
3
(
4
cos
3
θ
)
,
which with
cos
(
3
θ
)
=
4
cos
3
θ
−
3
cos
θ
becomes
x
3
−
4
3
r
2
x
−
4
1
r
3
cos
(
3
θ
)
=
0
.
Compare to the general cubic equation:
x
3
−
3
p
x
−
2
q
=
0
.
Equating these two gives
4
3
r
2
=
3
p
∴
r
=
2
p
,
and
4
1
r
3
cos
(
3
θ
)
=
2
q
∴
cos
(
3
θ
)
=
r
3
8
q
=
p
3
q
2
.
Consider a circle of radius
r
centered at 0 (contrary to what I stated before). Pick three points on that circle,
1
2
0
∘
apart from each other. Let
x
be the
x
coordinate of one of these points. Then
x
=
r
cos
θ
for a certain angle
θ
. Now
x
3
=
4
1
r
3
(
4
cos
3
θ
)
,
which with
cos
(
3
θ
)
=
4
cos
3
θ
−
3
cos
θ
becomes
x
3
−
4
3
r
2
x
−
4
1
r
3
cos
(
3
θ
)
=
0
.
Compare to the general cubic equation:
x
3
−
3
p
x
−
2
q
=
0
.
Equating these two gives
4
3
r
2
=
3
p
∴
r
=
2
p
,
and
4
1
r
3
cos
(
3
θ
)
=
2
q
∴
cos
(
3
θ
)
=
r
3
8
q
=
p
3
q
2
.
To show this recipe at work, consider the equation x 3 − 2 1 x − 2 0 = 0 . Then p = 7 , q = 1 0 . Thus r = 2 7 = 5 . 2 9 1 5 ; θ = 3 1 cos − 1 7 3 1 0 2 = 1 9 . 1 ∘ . This shows x 1 = 2 7 cos 1 9 . 1 ∘ = 5 . For the other two solutions, we add and subtract 1 2 0 ∘ : x 2 = 2 7 cos 1 3 9 . 1 ∘ = − 4 ; x 3 = 2 7 cos − 1 0 0 . 9 ∘ = − 1 .
Log in to reply
@Arjen Vreugdenhil – Note that this also gives the discriminant criterion. cos 3 θ = q 2 / p 3 is only possible if q 2 − p 3 < 0 . With the more conventional choice p ′ = − 3 p , q ′ = − 2 q this becomes the better known 4 ( q ′ ) 2 + 2 7 ( p ′ ) 3 < 0 for the case with three real solutions.
Log in to reply
@Arjen Vreugdenhil – This is a wonderful approach. I'm glad that I went through all the non-advanced problems (and their solutions) in the "Problems of the week" because I still managed to learn something by looking at easy problems like this.
You are an awesome person!
Now let me try to do a 4th degree polynomial version of this, which I pretty sure I will fail. 5th and above will definitely fail, right? Because not all roots of 5th degree polynomials can be expressed in closed form... Be right back, going to print out what you wrote and laminate it...
One liner? 3 2 + 5 + 3 2 − 5 = 3 ( 1 / 2 + 1 / 2 5 ) 3 + 3 ( 1 / 2 − 1 / 2 5 ) 3 = 1
2 + 5 = 8 1 + 3 5 + 3 ( √ 5 ) 2 + ( 5 ) 3 = 2 1 + 5 ^3
2 − 5 = 8 1 + 3 ( − 5 ) + 3 ( − 5 ) 2 + ( − √ 5 ) 3 = 2 1 − 5 ^3
Hence
3 ( 2 + √ 5 ) + 3 ( 2 − √ 5 ) = 2 1 + 5 + 2 1 − 5 =1
Right. By knowing the algebraic expression of ϕ 1 , ϕ 2 , ϕ 3 (and a few more powers), where ϕ denotes the golden ratio , it it is to identify that 2 + 5 = ϕ 3 and 2 − 5 = ϕ − 3 .
Nice work. Hypothetically speaking if the other quadratic factor has a non-negative discriminant, then the given expression will have multiple roots, right?
I only noticed that the two terms are golden ratios and they always add to 1. i.e. 1.618..... And -0.618...
I noticed that too, and could not figure out how these expressions turned out to be related to the golden ratio.
Log in to reply
Yes, read my comment under Chris James' solution above.
N N 3 N 3 N 3 N 3 N 3 + 3 N − 4 ( N − 1 ) ( N 2 + N + 4 ) = 3 2 + 5 + 3 2 − 5 = ( 3 2 + 5 + 3 2 − 5 ) 3 = ( 2 + 5 ) + ( 2 − 5 ) + 3 3 ( 2 + 5 ) ( 2 − 5 ) ( 3 2 + 5 + 3 2 − 5 ) = 4 + 3 3 − 1 N = 4 − 3 N = 0 = 0 .
Since the discriminant of x 2 + x + 4 is 1 2 − 4 ( 4 ) ( 1 ) = − 1 5 < 0 , there are no real solutions to N 2 + N + 4 = 0 . Thus, we conclude that N = 1 .