OctaGone Triangles
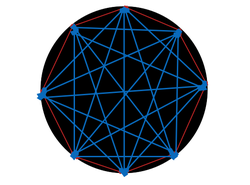How many triangles can be formed by joining the vertices of a regular octagon but not using any of its sides?
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry, its 8C3=56... By mistake i wrote 8c2
Log in to reply
FYI, you can edit your solution and comments, by clicking the pencil to the top right, and selecting edit.
Give it a try!
Log in to reply
I was thinking along the lines of a solution by "taking away" three vertices in between the vertices of the triangle to have the question turn into the number of triangles on a 8 − 3 = 5 sided shape with no restrictions. But the answer to that is 1 0 .
Is there any way for me to modify my argument to get the right answer?
Log in to reply
@Daniel Liu – Not quite, because your question is completely different.
In addition to the obvious PIE solution given above, my was:
- Label the vertices 1 to 8.
- WLOG, a vertex of the triangle is at 1 (will account for this later)
- There are
3
+
2
+
1
=
6
ways to pick non-adjacent vertices from
{
3
,
4
,
5
,
6
,
7
}
.
- However, each triangle will be counted thrice (ie we double counting).
- Hence, there are
8
×
6
÷
3
=
1
6
such triangles. (We multiple by 8 to account for the initial WLOG. We divide by 3 because we double counted)
This approach generalizes, to the n ≥ 6 -gon, and the number of triangles is
6 n × ( n − 5 ) × ( n − 4 )
Log in to reply
@Calvin Lin – Seems this is ambiguous, in that the problem as stated in words (joining the vertices) doesn't match the problem as shown in the diagram (only every other vertex has 5 lines to other vertices, the rest have three). Am I missing something?
Select one vertex and then observe there are 6 possible triangles. There are 8 vertices, and 6 * 8 = 48. However, going around through all 8 vertices, you replicate every possible triangle 3 times, so 48/3 = 16, the answer. Another puzzle is how many triangles if you allow the octagon's sides to be used. I get 21; do you agree?
Total number of triangles is 8 choose 2. Next, there are 8 pairs of vertices next to each other on the octagon. Each pair produces 5 triangles. 56-(5*8)=56-40=16
I don't agree with the "correct" answer. I have no idea what 8C2 or 8C3 or 4C1 mean in Jeet's solution. There is also a "sloppyness" in the drawing. Some small triangles show on one side of the octagon, but not the other side. I have ignored these "spurious" triangles (3, maybe 4 of them).
It's hard to talk about this problem without numbering the vertices. I chose to consider the figure as an 8-hour clock face, "8" at the top vertex and numbering the vertices consecutively from 1 clockwise starting from the first vertex to the right of the "8" vertex.
First, I considered the rays from "3" to "1" and from "3" to "8". Between these rays can be found 9 triangles formed with other rays from "1"(4) and "2"(5).
Then I considered the rays from "3" to "1" and from "3" to "7". Between these rays can be found 9 triangles formed with other rays from "1"(4) and "2"(5).
Then I considered the rays from "3" to "1" and from "3" to "6". Between these rays can be found 9 triangles formed with other rays from "1"(4) and "2"(5).
Then I considered the rays from "3" to "1" and from "3" to "5". Between these rays can be found 9 triangles formed with other rays from "1"(4) and "2"(5).
All of the vertices have a total of 288 triangles (9+9+9+9)*8. But 2/3's of them are duplicates (3 sides to a triangle;^)) so we only have 96 unique triangles, so far.
Then there are triangles that don't touch the vertices... 8 triangles touch the center of the octagon, but not the vertices. And 16 triangles touch these center triangles, but not the vertices. So, the total unique triangles is 120 (96+8+16). If we are supposed to include the "spurious" triangles, then add 3, or 4, to 120 to get 123, or 124.
I think its answer will be 24 not 16
As any 2 adjacent points can't be a side of triangle as per the condition given, we can take alternate points as vertices. So, fix any 2 alternate points and we get 3 possible points as 3rd vertex for each pair of such a alternate points.
Now, there are 8 such pairs. Thus, we get 3x8=24 triangles.
But, out of them every time 1 triangle is getting repeated. Therefore, 24-8=16 triangles.
Answer is 16.
Number of triangles formed with vertices of octagon =8C2 =56. Number of triangles formed with 1 side as side of octagon = 4C1 * 8= 32 ( 4C1 because 2 vertices are used for a chosen side and 2 more vertices are adjacent to the chosen side, else it would make a triangle with 2 sides as side of octagon. Therefore remaining vertices = 8-2-2=4) Number of triangles formed with 2 adjacent sides as side of octagon = 8. Therefore required number of triangles = 56- 32- 8 = 16