No one was able to solve it previously
If f ( x ) = x 3 − 2 3 x 2 + x + 4 1
Find ∫ 4 1 4 3 f ( f ( x ) ) d x
This problem is part of my set Some JEE problems
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Now there's a clever shortcut that I haven't seen before. Bravo!
Guessed that you may have special way but I think I couldn't have found the way you described after reading your solution.
Log in to reply
i have used ∫ a b f ( x ) . d x = ∫ a b f ( a + b − x ) . d x
Log in to reply
I have seen this in Brilliant for many times. Not obvious why negative sign is not needed at least for interchange of a and b. f(1-x) = 1 - f(x) seem to be very specific for this question and usually cannot be noticed unless getting to it.
Can you show how f(1- f(x)) = 1 - f(f(x)) and etc step by step? Could this method bring about incorrectness generally? When should we do in this way and what are the precautions?
Log in to reply
@Lu Chee Ket – first find f(1-x) which will surely come out to be 1- f(x) all ur queries will be over .Its not a property, we have just find a condition.
f ( x ) = ( x − 2 1 ) 3 + 4 x + 8 3 and ∫ 1 / 4 3 / 4 f ( f ( x ) ) d x = ∫ − 1 / 4 1 / 4 f ( f ( x + 2 1 ) )
Now f ( x + 2 1 ) = x 3 + 4 1 ( x + 2 1 ) + 8 3 = x 3 + 4 x + 2 1 i.e f ( f ( x + 2 1 ) ) = ( x 3 + 4 x ) 3 + 4 1 ( x 3 + 4 x ) + 2 1 = odd function + 2 1
So the integral equals to ∫ − 1 / 4 1 / 4 2 1 d x = 0 . 2 5
Nice......
@Pradeep Maurya You haven't put dx on 2nd integral of 2nd line
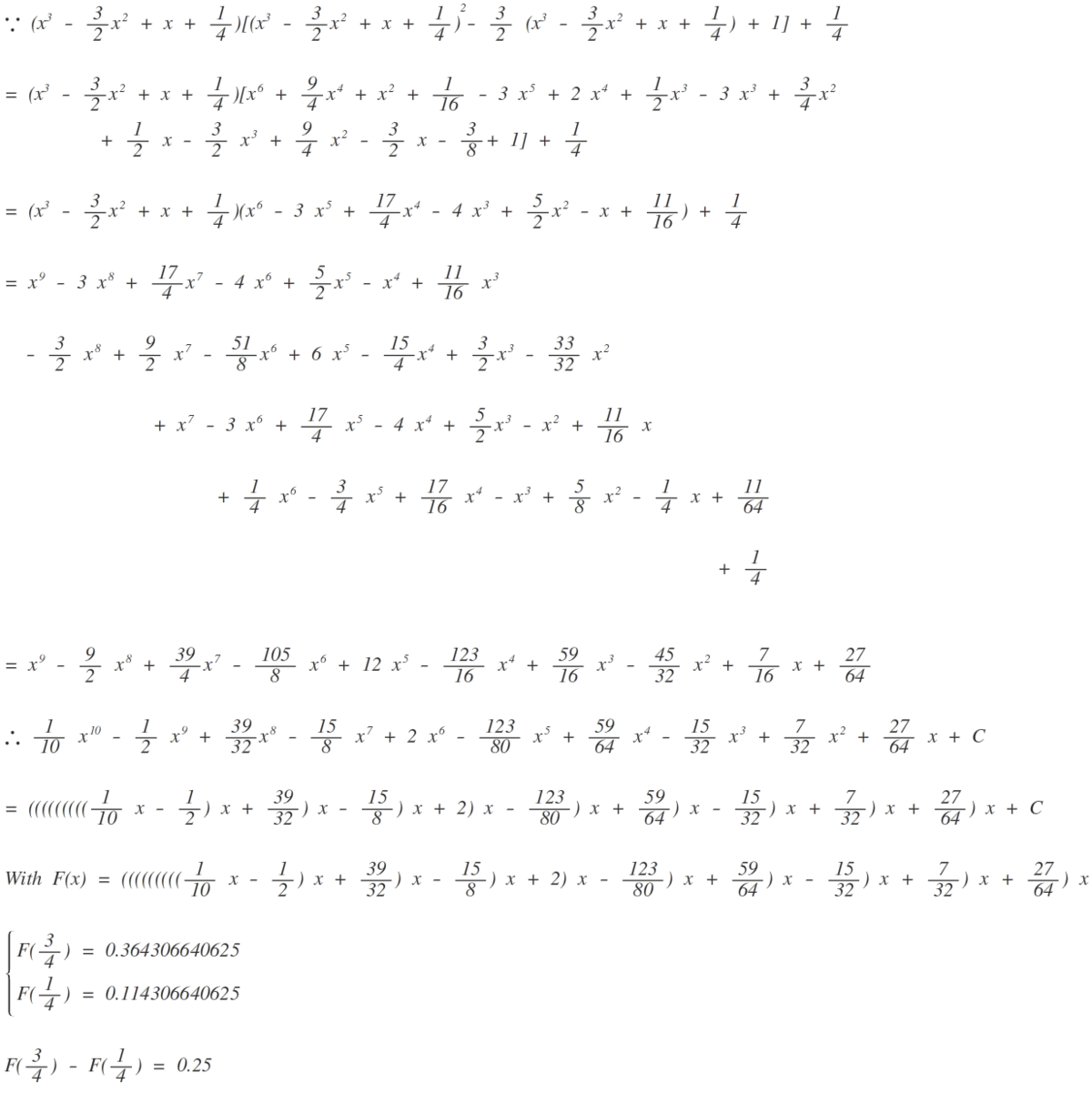
plz do upvote