No way out
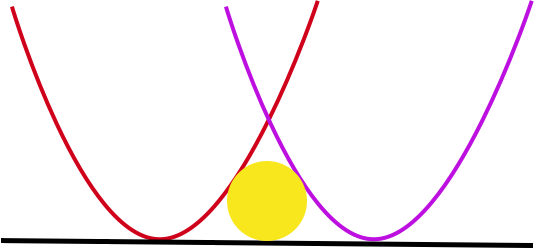 Let
S
be the region in the first quadrant which is
Let
S
be the region in the first quadrant which is
(i) to the right of the parabola y = x 2 and
(ii) to the left of the parabola y = ( x − 2 ) 2 .
Let r be the radius of the largest circle which can be inscribed in S . Find ⌊ 1 0 0 0 0 ∗ r ⌋ .
The answer is 3347.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Discussions for this problem are now closed
 Imgur
Imgur
Great problem Brian! Did basically the same thing except two minor time savers:
-
AT = AB . . . Tangents from an external point
-
Tangent to y = x 2 at T ( a , a 2 ) intersects the x axis at half the X coordinate i.e. A ( 2 a , 0 ) .
AT = AB and C x = 1
( a − 2 a ) 2 + ( a 2 ) 2 = ( 1 − 2 a ) 2
4 a 2 + a 4 = 1 − a + 4 a 2
a 4 + a = 1
Sir can you please explain why can't we do this way ??
A r e a o f r e g i o n S = 3 2 S o , f r o m t h i s w e g e t a n i n e q u a l i t y a s π r 2 ≤ 3 2 ⟹ r ≤ 0 . 4 6 0 6 5
Yes, that is the area of S , but the circle needs to be inscribed in S , and the value I found of r = 0 . 3 3 4 7 5 1 . . . is less than 0 . 4 6 0 6 5 . The circle with the solution radius is simultaneously tangent to the two parabolas and the x -axis.
Got it........Thanks for your kind reply sir
I use wolfram alpha. for finding root's of this Equation , But curious to know How to evaluate root's of this Equation ? , My Curiosity is also Increase More Because IIT JEE 2014 also asked an question on this Similar Equation (In it's own manner) :) @brian charlesworth
I can't see a "nice" way of finding the roots, but we could just use Newton's Method to find them manually, (although we would still rely on a calculator). Starting with an initial guess of 0 . 7 5 I got the correct value for a to 6 decimal places after just 3 iterations. I'm not sure if this would be an acceptable method for the IIT JEE but it's the only way I can think of.
That's Interesting ! And Sir what is Newton Method ? I really Hearing it first Time, Sorry to disturb you ! And Actually It doesn't needed in JEE to calculate root's , Actually They asked question about the Nature of root's of equation ( x^4+x =a ) and etc .
@Deepanshu Gupta – Newton's Method is an iterative process for finding successively better approximations for the real-valued roots of a function f ( x ) . The iterative formula for the ( n + 1 ) st approximation x n + 1 is
x n + 1 = x n − f ′ ( x n ) f ( x n ) .
You have to make an educated "guess" for x 1 by drawing a rough graph and testing out a few values, after which you just keep plugging one approximation into the formula after the other other until you get a suitable degree of accuracy.
So with this problem we have f ( x ) = x 4 + x − 1 , giving us f ′ ( x ) = 4 x 3 + 1 . Noting that f ( 0 . 5 ) = − 0 . 4 3 7 5 and f ( 1 ) = 1 we make a first guess of x 1 = 0 . 7 5 and plug this into the formula to find that
x 2 = 0 . 7 5 − 2 . 6 8 7 5 0 . 0 6 6 4 0 6 = 0 . 7 2 5 2 9 0 7 .
Plugging in successive approximations in turn, we find that
x 3 = 0 . 7 2 4 4 9 2 7 , x 4 = 0 . 7 2 4 4 9 1 9 , x 5 = 0 . 7 2 4 4 9 1 9 .
So after just a few iterations we have a root that is accurate to 6 decimal places, namely 0 . 7 2 4 4 9 2 . (It really helps to make a good first guess. :)) An explanation of the formula is given here .
As for the JEE asking for the "nature" of the roots, I think that they are looking for a more general description, i.e., the number of real roots and whether these are positive or negative. For this you can use Descartes' Rule of Signs , which is helpful but far from definitive.
@Brian Charlesworth – That is really Very Interesting ! Thanks For The Help Sir !
@Deepanshu Gupta – You're welcome. :)
Woah... The rating shot up like a rocket. By the way, there is a purely algebraic solution and thats how I solved it. But its tedious.
These questions made by you makes me realise how important is wolfram alpha.
These problems inspire me to fit a circle between 2 random curves :p. Nice problem sir :)
Thanks. I don't know how I got around to posting so many "fit the circle" questions, but once I think one up I'm always curious about what equation needs to be solved at the end of the process. I'll be interested to see what kind of "fit the circle" question you come up with. :)
@Brian Charlesworth – You always come up with nice "Fit the circle" problems and I love them! Awesome!
@Brian Charlesworth – There is a formula for circumradius
R = 4 1 ( s − a ) ( s − b ) ( s − c ) ( s − d ) ( a b + c d ) ( a c + b d ) ( a d + b c )
But this is bit nasty.
Oops..posted in wrong problem, I wanted to post in quadrilateral problem.
@Krishna Sharma – That's a useful formula; thanks for mentioning it. Although it is long, it has a nice symmetry to it so it's not too hard to remember. I tried it on the cyclic quadrilateral problem and got the expected value of R . :)
Haha. Yes, well, when I think up these questions I always hope that there will be a "nice" solution, but I don't worry about it now if that's not the case. If at the end of the solution process a quick application of the WolframAlpha "tool" is needed then I'm fine with that. :)
Assume a is radius of inscribed circle, it is easy to see that the centre of this circle on the line x=1: ( x − 1 ) 2 + ( y − a ) 2 = a 2 ( x − 1 ) 2 = a 2 − ( y − a ) 2 y = ( a 2 − ( x − 1 ) 2 ) + a a 2 − ( x − 1 ) 2 + a < x 2 a 2 − ( x − 1 ) 2 < x 2 − a ( a 2 − ( x − 1 ) 2 ) < ( x 2 − a ) 2 a 2 − ( x − 1 ) 2 < x 4 − 2 a x 2 + a 2 x 4 − 2 a x 2 + ( x − 1 ) 2 > 0 a < ( x 4 + ( x − 1 ) 2 ) / ( 2 x 2 ) = ( 1 / 2 ) ( x 2 + 1 − 2 / x + 1 / x 2 f ( x ) = x 2 + 1 − 2 / x + 1 / x 2 f ′ = 2 ∗ x + 2 / x 2 − 2 / x 3 f(x) changes its sign at the point has x-cord is: x = 0 . 7 2 5 ; f ′ > 0 ; f m i n = 0 , 3 3 4 7 5 1 , ⌊ 1 0 0 0 0 ∗ r ⌋ = 3 3 4 7
The parabolas intersect at ( 1 , 1 ) , so the coordinates of the inscribed circle will be ( 1 , r ) .
Now look at the point ( a , a 2 ) on the curve y = x 2 such that the normal to the curve at this point passes through ( 1 , r ) . (By symmetry we only need to look at the "relationship" between one of the parabolas and the inscribed circle.) Since the slope of the curve at this point is 2 a , the equation of the normal will be
y − a 2 = ( − 2 a 1 ) ( x − a ) ,
and since this will pass through ( 1 , r ) we have that
r − a 2 = ( − 2 a 1 ) ( 1 − a ) , (i).
Also, we know that the distance between ( a , a 2 ) and ( 1 , r ) is r , and so
( 1 − a ) 2 + ( r − a 2 ) 2 = r 2 , (ii).
Combining equations (i) and (ii) we have that
( 1 − a ) 2 + ( − 4 a 2 1 ) ( 1 − a ) 2 = ( a 2 − ( 2 a 1 ) ( 1 − a ) ) 2
⟹ ( 1 − a ) 2 = a 4 − a + a 2 ⟹ a 4 + a − 1 = 0 ,
which by numerical methods has the positive real solution a = 0 . 7 2 4 4 9 1 9 5 9 . . . , which, when plugged into equation (i), yields the value r = 0 . 3 3 4 7 5 1 . . . .
Thus ⌊ 1 0 0 0 0 ∗ r ⌋ = 3 3 4 7 .