Split, Split, Split

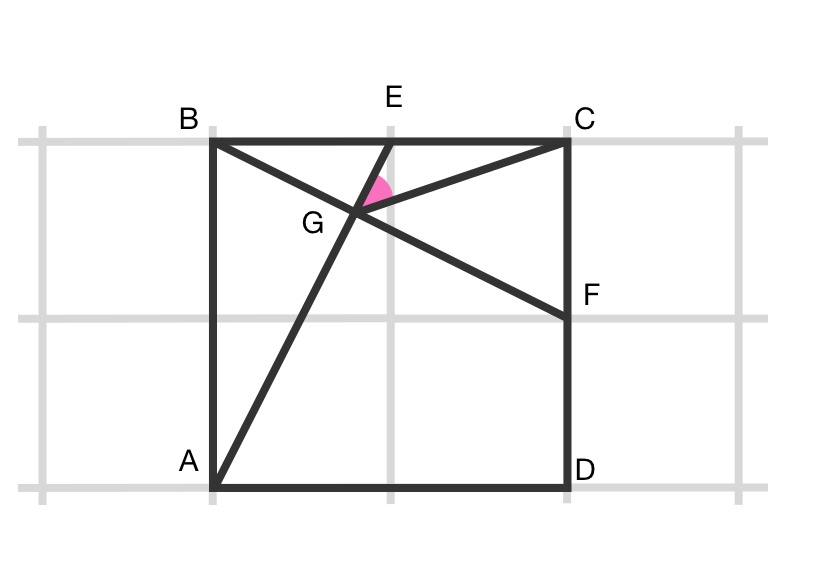
Label the vertices as shown above.
Observe that $AE \perp BF$ (which can be shown by calculating the product of their tangents)
Since $\angle EGF = 90^ \circ$ and $\angle ECF = 90 ^ \circ$ , thus $\angle EGF + \angle ECF = 180^ \circ$ so $ECFG$ is a cyclic quadrilateral.
Thus, $\angle EGC = \angle EFC$ . Since $ECF$ is an isosceles right triangle, thus $\angle EFC = 45 ^ \circ$ .

Nocturne No.3 Commentary

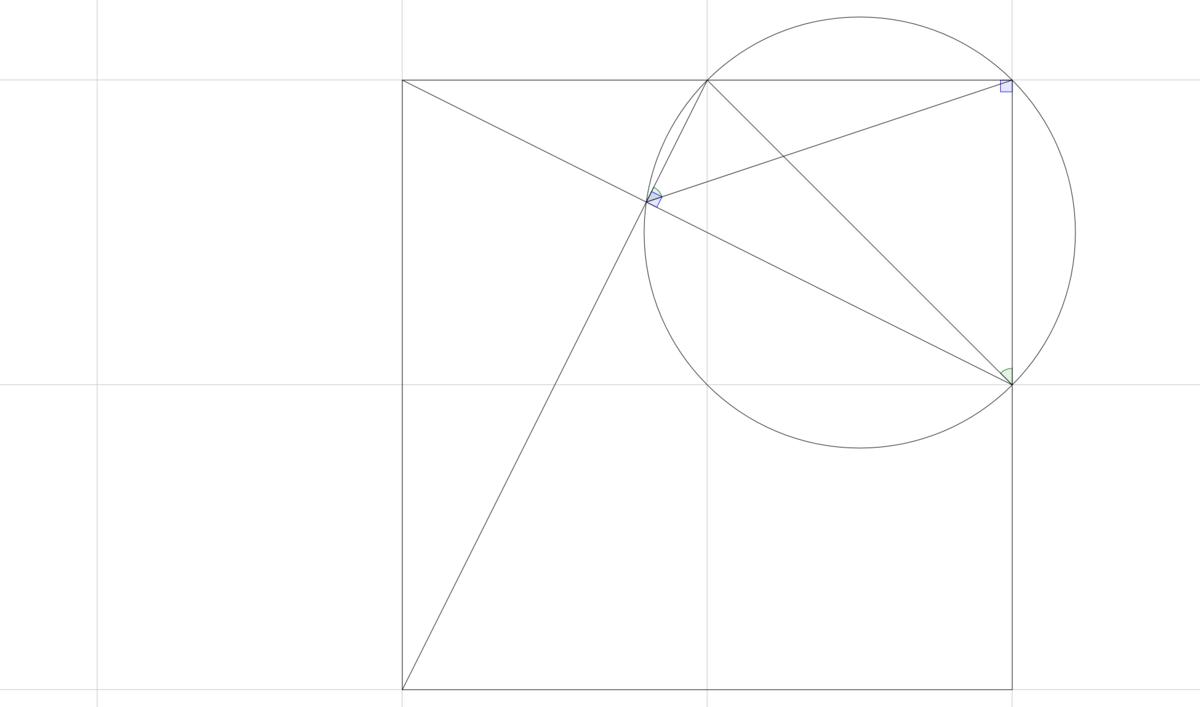
Notice how a line segment is added to form two right triangles.

The diameter of every right triangle's circumcircle is its hypotenuse. (converse of Thales' theorem )

Since the two right triangles share the same hypotenuse, they share the same circumcircle.

<OR since the opposite angles of the quadrilateral composed of the two right triangles are supplementary i.e. add up to 180 degrees, the vertices of the right triangles are concyclic .>

The required angle can then easily be found via angles in the same segment (angles subtended by the same segment are the same).

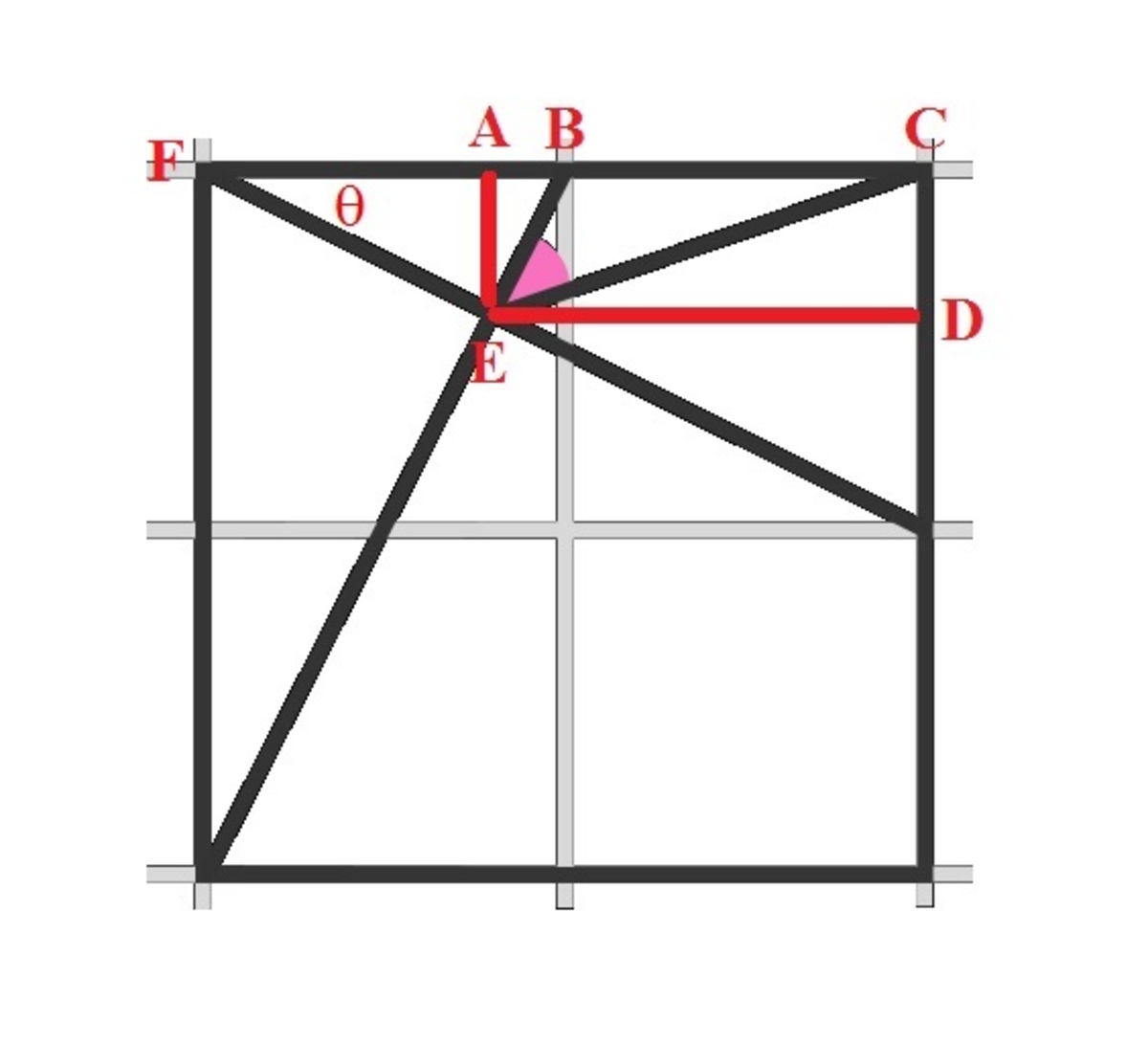
Let $\angle AFE = \theta$ and note that $\tan \theta = \frac 12$ . Since $FA = 1$ , then $BE = FA \sin \theta = \frac 1{\sqrt 5}$ . $AB = BE \sin \theta = \frac 15$ and $AE = BE \cos \theta = \frac 25$

Now, we have:

$\begin{aligned} \angle BEC & = \angle BED - \angle CED \\ & = \tan^{-1} \frac {AE}{AB} - \tan^{-1} \frac {CD}{ED} \\ & = \tan^{-1} \frac {\frac 25}{\frac 15} - \tan^{-1} \frac {\frac 25}{1+\frac 15} \\ & = \tan^{-1} 2 - \tan^{-1} \frac 13 \\ & = \tan^{-1} \frac {2-\frac 13}{1+\frac 23} \\ & = \tan^{-1} 1 \\ & = \boxed{45}^\circ \end{aligned}$