Nodes and triangles
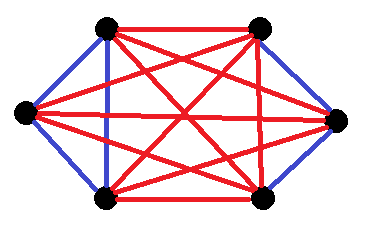
Suppose you interconnect 6 nodes such that every node has an edge going to all the other nodes. Each edge is colored either red or blue (at random).
Call a "complete triangle" one formed by 3 nodes where all the edges are the same color.
Will there always be at least two complete triangles?
With this example, an all-red triangle and an all-blue triangle are marked.
Note: The triangles are allowed to both be the same color , and they are allowed to re-use the same edges as long as at least one of the edges is different.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Pretty sure w 1 , w 2 , w 3 should be v 1 , v 2 , v 3 .
Log in to reply
Well, moving from the first paragraph to the second, ( w 1 , w 2 , w 3 ) could be any one of ( v , v 1 , v 2 ) , ( v , v 1 , v 3 ) , ( v , v 2 , v 3 ) or ( v 1 , v 2 , v 3 ). I started the labelling system afresh in the second paragraph!
Log in to reply
Oh, that makes sense.
But it seems like you forgot it after you introduced w i , since you go back to using v i .
Log in to reply
@Malte Juhl – To make the notational disconnect between the first and second paragraphs clear, I have relabelled the vertices in the first paragraph.
For the sake of completeness, this is called the "theorem on friends and strangers". A special case of Ramsey's theorem.
I have got a better solution, even if in a momentary jeopardy i clicked on "No".
for n vertices, n ≥ 6 we have at most 2 ( n − 2 ) edges, none of which makes a triangle. for no triangle of same coloured edges, we can have all these 2 ( n − 2 ) edges of same colour and rest to be different. These 2 ( n − 2 ) edges are formed by connecting any two of the vertices with (n-2) other vertices, such they are not connected, and no cycles are made. The number of pairs will be: ( n − 2 ) + 2 ∗ ( n − 3 ) + ( n − 2 ) . . + 2 + 1 = n − 2 + ( n − 3 ) ( n − 2 ) = n 2 − 4 n + 4 . Even if the rest of the n C 2 − 2 ( n − 2 ) edges are coloured different, there will be at least two triangles made by these rest of the triangles when n ≥ 6 .
Simply because, there are a total of 2 0 triangles for n = 6 , and 1 5 edges. we can get at most 2 ∗ 4 = 8 edges that do not make any triangle. There has to be n C 2 − 2 ( n − 2 ) edges = ( 7 here) left, that will make triangles with the n 2 − 4 n + 4 pairs of edges(= 1 6 here) , and 6 n 3 − 9 n 2 + 2 6 n − 2 4 ( = 4 here) triangles more to be identified. These triangles are already made... So, we made these 4 triangles out of 7 additional edges of same colour. But one triangle requires 3 edges, we can make at most 2 triangles from 5 edges (on an Euclidean plane).. and can make the rest 2 triangles from 1 additional edge only with the help of these already constructed 5 edges. = 6 edges has made these additional 4 triangles.
number of these will increase with increase in n , because the availability of residual triangles increases more than the number of residual lines with increase in n .
The 2(n-2) edges formula is plain wrong. With n=6 vertices, you can split them in 3+3, and draw all 9 (3x3) edges from any of the 1st set of 3 vertices, to any of the 2nd set of 3 vertices. That makes 9 edges, and you don’t have any triangles. A triangle would require jumping from the 1st set to the 2nd set and back to the 1st set, or vice versa . . . however. the vertices within a given set are not connected. 9 > 8 ( from 2(6-2) ) so there’s clearly something wrong.
Consider a node A . WLOG, assume it connects to ≥ 3 blue edges. In the ≥ 3 nodes that A connects to: if any connect to each other with a blue edge, then we have formed a triangle; if all of them connect to each other with red edges, then we have again formed a triangle. Therefore, there exists ≥ 1 triangle.
WLOG, start with a blue triangle:
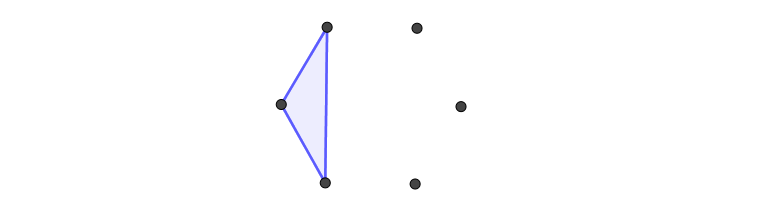 To avoid generating a new triangle (using the method described previously) from a disconnected node, that node must use red edges to connect to the
3
nodes currently making a triangle, and use blue edges to connect to the remaining nodes (see comments). Hence, we get this:
To avoid generating a new triangle (using the method described previously) from a disconnected node, that node must use red edges to connect to the
3
nodes currently making a triangle, and use blue edges to connect to the remaining nodes (see comments). Hence, we get this:
 and we find that we have made
2
triangles.
and we find that we have made
2
triangles.
Moderator note:
As pointed out in the comments, we cannot simply work from a "worst case scenario" of a differing scenario. It might be possible that a different initial setup could lead to a different result.
What if while randomly colouring the edges you end up with a perimeter all red and the internal connections all blue, no triangles exist then. Or is this scenario not possible?
Log in to reply
In that scenario, you have two blue “equilateral” triangles, each joining up alternate vertices.
Why must a disconnected node use red edges to connect to the 3 nodes currently making a triangle?
What if all the nodes are arranged in a line - the question doesn’t prohibit this - then there are no triangles.
Log in to reply
I believe the question is defining a triangle as three nodes joined together by lines, or a set of three nodes, rather than the traditional geometric definition (as I believe this question falls under the purview of graph theory).
Agreed, it should be made clear in the question.
But in the current picture two of the edges are neither blue nor red, but black which makes it impossible to guess what colour were they originally supposed to be.
It's a bit more complicated than that. Why couldn't you have one blue edge and two red edges from a new node to the old ones? You have said they all have to be red, which is not necessarily true.
Log in to reply
Because then a new triangle will be formed from that new node C and 3 other nodes. Either ≥ 1 red edges connects from that C to another new node D , which generates a new triangle using the 2 red old nodes, C and D ; or 2 blue edges connects from C to new nodes E and F , which generates a new triangle using the blue old node, C , E and F .
Log in to reply
Yes (as I showed in my proof)! But this means that the argument is more complicated than your presentation implies. There are several other ways in which we can obtain two monochromatic triangles, and your argument (as currently expressed) does not show these.
If we had all the sides of the exagon blue and all the diagonals red (or the opposite) none of the triangles would be complete.
Log in to reply
See the first comment.
We have 2 big red triangles from nodes 135 and nodes 246
The answer of this question is yes .
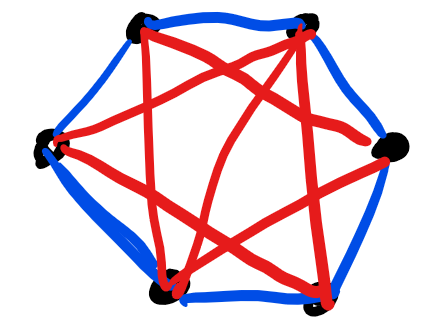
To show why, let's try to connect all of the six vertices without creating two triangles. The TED-Ed video that answers a similar problem explains why you will always have at least one complete triangle with six vertices. So WLOG, let's create that triangle as follows:
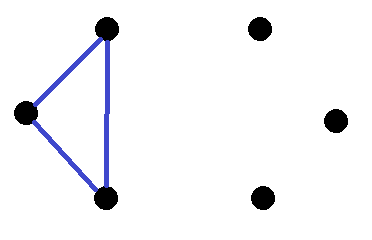
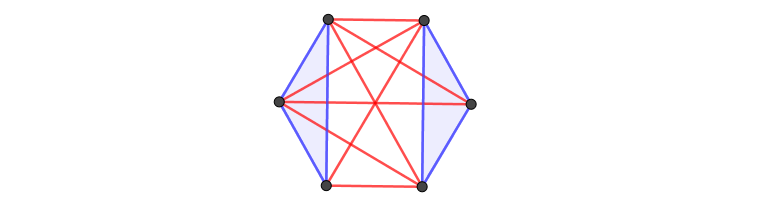
We're going to call the three nodes on the left that already form a triangle the left nodes and the three on the right that currently have no edges the right nodes. Each of the right nodes must connect to all of the left nodes. If a specific right node connects to the left nodes with 2 or 3 blue lines we create a second blue triangle, which is what we want to avoid. So let's connect each of the right nodes to all of the left nodes with only red edges. That way we don't created any new triangles. Plus, we just gave ourselves some extra freedom. For each of the three right nodes we may freely change one of its edges to blue later on without creating any new triangles. We now have the following:
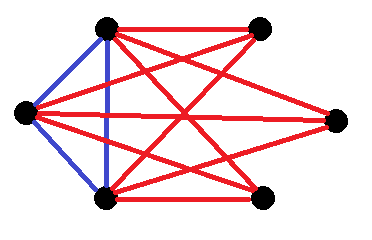
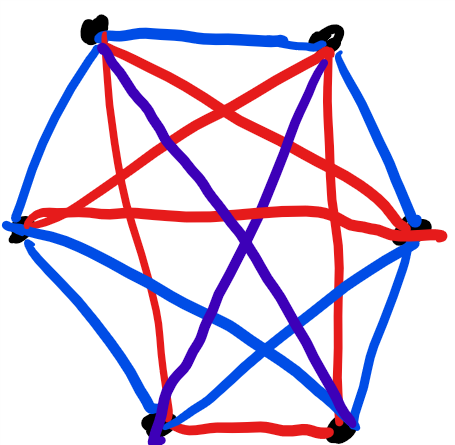
We only need to connect the three right nodes with each other. If we make all of those edges blue we just created a second triangle, so we can't do that. If we make two or three of the edges red we create very many red triangles, so we also can't do that. There's only one thing to do: create two blue edges and one red edge. WLOG, let's connect the top-right and the bottom-right nodes with that red edge:
This creates three red triangles. But no worry, earlier we gave ourselves the freedom to change 3 red edges to blue, so let's use them to get rid of those triangles. We can use the one for the top-right node to destroy one red triangle, the one from the bottom-right node to destroy the second and finally we use the one of the right node to destroy the third tri.... wait. None of the red triangles we have uses the right node, so changing one of its edges to blue won't help.
That means we have to accept that no matter how you color the edges, there will always be at least two complete triangles, so the answer is yes . □
very ridiculous problem
What would be the answer for an n-sided polygon?
C 6 2 = 15 edges, C 6 3 = 20 triangles.
Suppose vertex v i is connected by r i ( 0 ≤ i ≤ 5 ) red edges and ( 5 − r i ) blue edges. Because r i , 5 − r i ≤ 6 , the number of heterochromatic angles (angles have two different colored sides) ≤ 6 ∗ 6 = 3 6 . And because one heterochromatic triangle has two heterochromatic angles, the number of those triangles ≤ 1 8 . Thus the number of complete triangles ≥ 2 0 − 1 8 = 2 .
Wow, that’s really systematic!
There are at least 2 triangles. We can prove it by writing an algorithm guaranteed to "find" the other triangle based on the first triangle.
We already know there's at least one triangle. Label the nodes of that triangle A , B and C . We also assume WLOG (without loss of generality) that the triangle is red.
Consider the triangle formed by the remaining nodes. It is either a red triangle, a blue triangle, or neither. If it's a red or blue triangle, we have our 2nd triangle. Otherwise, there must be at least 1 blue line and 1 red line in the triangle. Look at the blue line (if there are 2 blue lines just pick either one), and label the nodes at each end D and E .
Consider lines AD , BD and CD . If any 2 of them are red, then we have our 2nd red triangle. Otherwise, at least 2 of them are blue.
Assume WLOG that AD and BD are blue. If AE is blue, then we have a blue triangle in ADE . Similarly, if BE is blue, then we also have a blue triangle in BDE . Otherwise, AE and BE have to be red. But then we would have a 2nd red triangle in ABE .
So there will be a 2nd red triangle or a blue triangle no matter what.
To simplify, the hexagon shape can only be filled with the following:
Since can be the colour reflection, we can remove the duplication as such we only need to do 6 blue, 5 blue 1 red, 4 blue 2 red and 3 blue 3 red shapes. Rotate symmetrical shapes are taken out as well as they form the same triangles.
Before drawing we have to obey these 2 rules: Rule 1: The internal lines are drawn opposite so that we do not make a coloured triangle. Rule 2: Purple lines are drawn to act as a wild colour which can replace red or blue lines
For 6 blue as you can see if any red lines change to blue it becomes a blue triangle, the red lines form at least 2 triangles.
For 5 blue 1 red, whereby if it is red or blue it forms a red triangle or blue triangle respectively. Therefore form 2 coloured triangles.
For 4 blue 2 red, the combination is
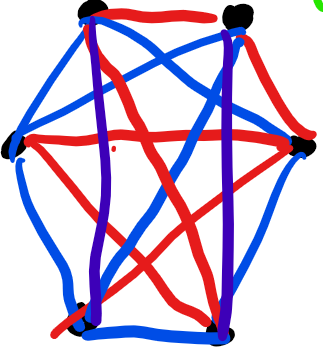
or
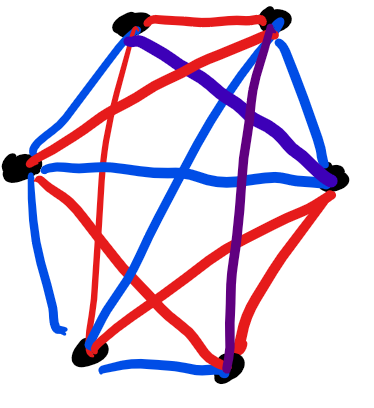
or
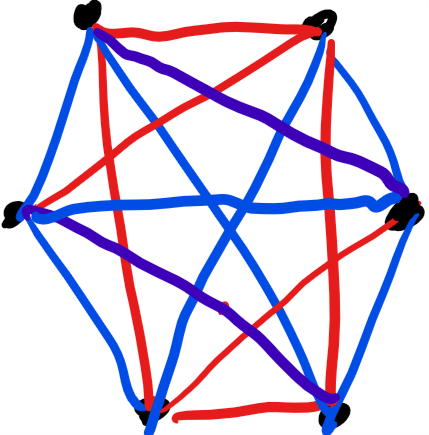
last but not least
For 3 blue 3 red, the combination is
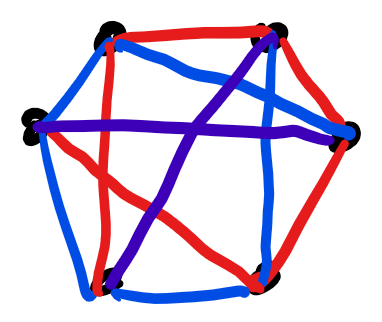
or
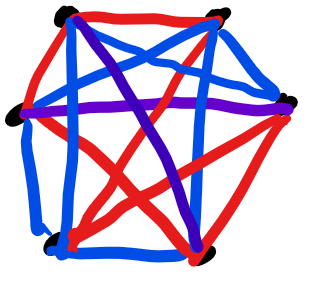
or whereby we reverse engineered and draw a few blue lines
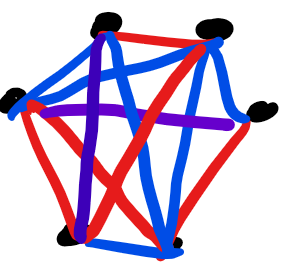
Why are there black edges in the diagram? Am I missing something?
SVG export a little off. I fixed it, thanks!
What if all 6 nodes are lined up?
Log in to reply
It's still the case that "every node has an edge going to all the other nodes".
In actual practice, if this ever happens, usually the edges get drawn curved.
Log in to reply
But you can't make triangles out of them
Log in to reply
@Diego González – By the definition, yes, you can have triangles: Call a "complete triangle" one formed by 3 nodes where all the edges are the same color.
Pick any vertex z . It connects to five other vertices, and so at least three of the edges coming from it must be of the same colour. Suppose, for definiteness, that three vertices z 1 , z 2 , z 3 are connected to z with red edges. If any two of these vertices, say z i and z j , are connected by a red edge, then z , z i , z j is a red triangle. Thus no two of these vertices are connected by a red edge, and hence z 1 , z 2 , z 3 is a blue triangle. Thus at least one monochromatic triangle exists.
However we have found them, suppose that the vertices w 1 , w 2 , w 3 are connected by a monochromatic triangle. For definiteness, suppose that this triangle is red. Suppose that there are no other red triangles. If u 1 , u 2 , u 3 are the other three vertices, then two of them must be connected by a blue edge (otherwise we would get a new second red triangle). Suppose that the edge u 1 u 2 is blue. If any two of the edges connecting u 1 to v 1 , v 2 , v 3 were red, say u 1 v i and u 1 v j , then u 1 , v i , v j would be the vertices of a red triangle. Thus at least two of the edges u 1 v 1 , u 1 v 2 , u 1 v 3 must be blue. Similarly, at least two of the vertices u 2 v 1 , u 2 v 2 , u 2 v 3 must be blue. Consequently there must be some 1 ≤ k ≤ 3 such that u 1 v k , u 2 v k are both blue, and hence u 1 , u 2 , v k are the vertices of a blue triangle. Thus we have found a blue triangle.
Thus there are always at least two monochromatic triangles.