Non-classical series on Central binomial coefficients
Evaluate 4 n = 0 ∑ ∞ ( 4 n + 1 ) 2 ( 2 + 4 n ) 2 1 6 n ( 2 n 4 n ) − 1
The challenging task is to find the closed form for the above series.
This problem is original which I happened to discover while writing an article ( mentioned in solution section) .
The answer is 1.014699.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Pi Han Goh Sir
Log in to reply
Wowwww! You should tag @Mark Hennings , he is incredibly good at this! I'm a newbie when it comes to these G and Li2.
Log in to reply
Oh! I see. Thank you sir.
Hi @Pi Han Goh Sir , Can you help to confirm the answer for the following series? n = 0 ∑ ∞ 1 6 n ( n + 1 ) H n ( 2 n 4 n ) . My closed form says the approximated answer to be 1 . 9 8 3 0 6 4 5 6 3 7 0 3 4 1 6 9 3 9 0 1 2 1 9 0 3 9 7 3 5 2 5 8 4 0 8 0 6 2 8 6 6 6 5 4 7 5 2 9 7 8 7 7 6 0 5 8 9 1 8 8 0 4 1 4 . . . however, with Wolfram alpha check for the 4 6 1 9 terms, it generates the approximation to 1 . 8 5 3 7 6 1 3 3 0 3 3 6 2 5 7 6 0 7 3 5 3 7 8 4 5 8 6 3 8 4 1 6 5 1 3 8 9 1 2 6 5 0 4 8 8 6 3 7 1 1 1 4 9 5 4 2 8 0 9 0 7 6 3 5 . . . . If I go above or randomly consider any higher terms the approximation due to WA is 1 . 6 4 . . . For n = 4 6 1 9 here is and for higher terms here is.
Since I dont know how to use python and mathematical tools .Can you help to confirm the right answer via computer check or by python? Thank you
Log in to reply
@Naren Bhandari – I took the convention that H 0 = 0 .
Here's the sum for n = 0 to n = 1 0 4 :

The final term of this sum is equal to this value , which is approximately equal to:
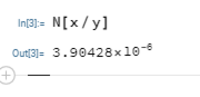
which agrees with the latter portion of the Python code, so I'm fairly confident that the infinite series is equal to 1.889 to 3 decimal places.
Log in to reply
@Pi Han Goh – On the other hand, Mathematica agrees with your result.

which simplifies to 3 8 [ ln ( 4 8 − 3 2 2 ) + 2 ln ( 8 − 2 ) ]
So I'm rather confused right now...
You should really summon Mark Hennings on this one. Try creating a separate note for this....
Based on the Python result and the Mathematica result, I now believed that the series converges super duper slowly to 1.98....
Log in to reply
@Pi Han Goh – Thank you soo much, Sir for the help. I too got the same result generated by mathematica. I will surely make notes on these sorts of series. Moreover, I have established such generating function for Bino-Harmonic series. :) (for instance here ). I believe such a slow growth of series is due to harmonic involved.
The exact answer for the proposed problem is as follow
The full proof of the series is developed here in my article( see Theorems and proofs for some special Cases on page no 16-18) at Researchgate.
The interesting things is to note that the sum attains the heavy weight of hypergeometric expression which are indeed undoable and the work performed in the article leads to answer those hypergeometric expressions in elementary manner.