NonTraditional Lilypads

Model the situation as an arrangement of the letters $ABC$ .

• A jump does not change the arrangement of $ABC$ .

• A leap results in swapping two neighboring letters. The empty leaf must be on either side of the two letters to be swapped. Thus $A|BC| \mapsto A|CB|$ . (The vertical bar indicates the possible position of the empty leaf. After the leap, the vertical bar is in the other position: $A|BC \mapsto ACB|$ and $ABC| \mapsto A|CB$ .)

Since we wish to go from $CBA$ to $ABC$ , three leaps are needed at least:

$CBA \mapsto BCA \mapsto BAC \mapsto ABC\ \ \ \text{or}\ \ \ CBA \mapsto CAB \mapsto ACB \mapsto ABC.$

However, two leaps in a row has zero effect; e.g. $AB|C \mapsto |BAC \mapsto AB|C$ . We may therefore ignore solutions with two leaps in a row, and assume that every leap (except perhaps for the last) is followed by at least one simple jump. This results in at least five moves. Moreover, at any time at most one simple jump is needed to get the empty leaf in the right position for the next leap. Thus the shortest solution will be of the form $\text{(jump) - leap - jump - leap - jump - leap - (jumps)}.$

At this point we have proven that the solution consists of at least five steps.

If we skip the first jump, we start by swapping $CBA \mapsto CAB$ , and the last swap will be $ACB \mapsto ABC$ , leaving the empty leaf next to either $B$ or $C$ ; at least one additional jump is needed.

At this point we have proven that the solution consists of at least six steps.

We find a solution in six steps: $CBA| \mapsto C|AB \mapsto |CAB \mapsto AC|B \mapsto ACB| \mapsto A|BC \mapsto |ABC.$ Alternatively, we can perform one jump at the beginning and follow the alternative route with $CBA \mapsto BCA$ . In that case, it can be arranged that no jumps are needed at the end. This gives another solution in six steps: $CBA| \mapsto CB|A \mapsto |BCA \mapsto B|CA \mapsto BAC| \mapsto BA|C \mapsto |ABC.$

We have now shown that there are solutions with six steps.

To create a min bound for the solution, I will prove the minimum number of jumps and the minimum number of leaps separately.

First, I will prove the min. number of jumps. Notice that all frogs start an odd number of lily pads away from their final position, and that leaping over a frog moves them an even number of lily pads. We therefore find that each frog must jump at least once to reach it's destination, so the minimum number of jumps is $\boxed{3}$ .

Now, consider the minimum number of jumps. Each time a frog jumps, you switch positions of two adjacent frogs. It is easy to see that the quickest way to quickly sort the frogs CBA takes $\boxed{3}$ moves, so I will not bother making a more formal explanation.

Therefore, at best, we can solve this problem in 3 + 3 = $\boxed{6}$ moves.

This is possible by the method posted by Arjen.

$CBA| \mapsto CB|A \mapsto |BCA \mapsto B|CA \mapsto BAC| \mapsto BA|C \mapsto |ABC.$

We'll run breadth-first search (bfs) on this configuration space for the shortest solution:

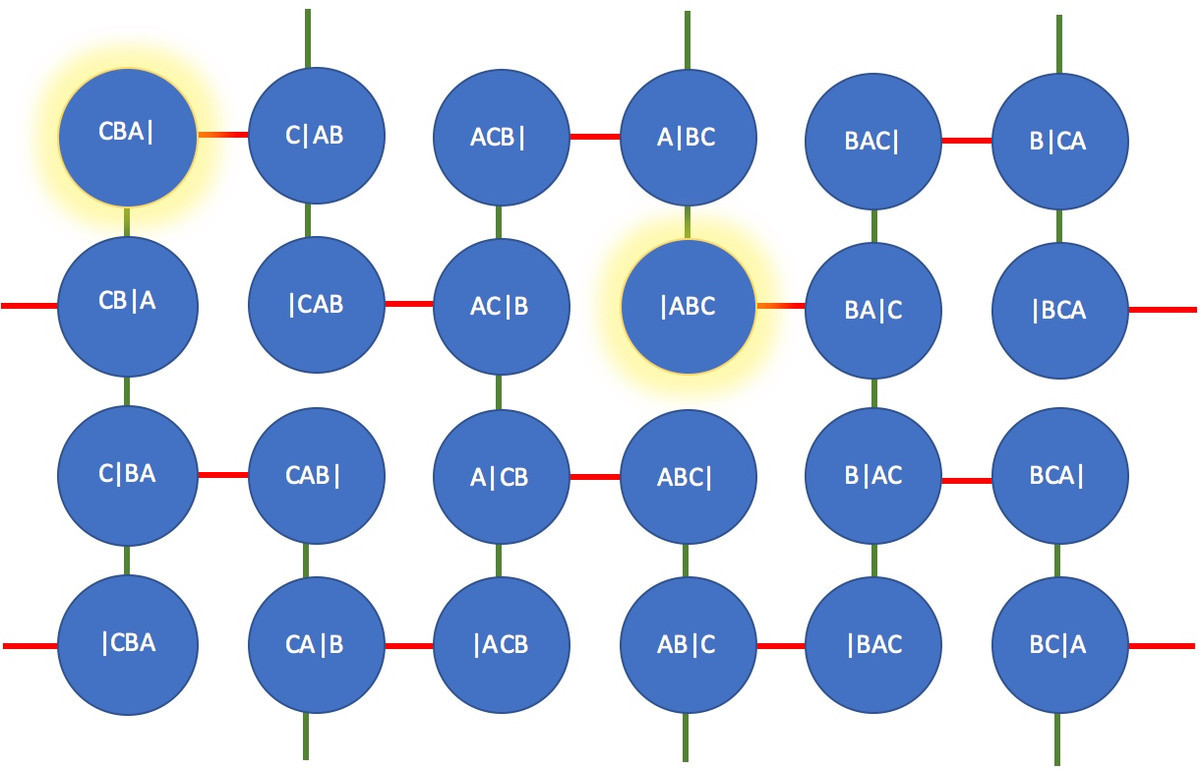(image taken shamelessly from Arjen's solution)

In this graph, each node represents a possible configuration of frogs and there is an edge if it is possible to go from one node to another in just one jump. Here is how we plan to explore this space:

• Start at the initial configuration
• Go to all possible configurations at distance 1 from this configuration.
• From the last set of configurations reached, go ahead one more step, so as to reach all possible configurations at distance 2.
• Repeat the last two steps until you reach the target configuration.

It is easy to see that this must indeed find the shortest distance between the start and the target configurations.

We encode the states as follows:

1
2

start = ([3, 2, 1, None], 3) # the empty lilypad is at position 4
goal = ([None, 1, 2, 3], 0)

and here is how we define the jumps:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

def jump(state):
    frogs, empty = state
    N = len(frogs)
    if empty > 0:
        new_state = frogs[:]
        new_state[empty], new_state[empty-1] = new_state[empty-1], new_state[empty]
        yield (new_state, empty-1)
    if empty > 1:
        new_state = frogs[:]
        new_state[empty], new_state[empty-2] = new_state[empty-2], new_state[empty]
        yield (new_state, empty-2)
    if empty < N-1:
        new_state = frogs[:]
        new_state[empty], new_state[empty+1] = new_state[empty+1], new_state[empty]
        yield (new_state, empty+1)
    if empty < N-2:
        new_state = frogs[:]
        new_state[empty], new_state[empty+2] = new_state[empty+2], new_state[empty]
        yield (new_state, empty+2)

and then, we implement the search:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def solve_frogs(start, goal):
    closed_set = set()
    open_queue = Queue()

    parents = {}

    open_queue.put(start)

    while not open_queue.empty():
        current_state = open_queue.get()
        closed_set.add(str(current_state))
        if current_state == goal:
            print "goal reached!"
            break
        for successor in jump(current_state):
            if str(successor) not in closed_set:
                open_queue.put(successor)
                parents[str(successor)] = current_state

    path = []
    state = goal
    while True:
        path.append(state)
        if state == start:
            break
        state = parents[str(state)]
    path.reverse()

    return path

And, finally to get the path:

1
2
3
4
5
6
7
8
9

path = []
state = goal
while True:
    path.append(state)
    if state == start:
        break
    state = parents[str(state)]
path.reverse()
print path

That gives

1
2
3
4
5
6
7

[([3, 2, 1, None], 3),
 ([3, None, 1, 2], 1),
 ([None, 3, 1, 2], 0),
 ([1, 3, None, 2], 2),
 ([1, 3, 2, None], 3),
 ([1, None, 2, 3], 1),
 ([None, 1, 2, 3], 0)]

Let pad 1 be the pad frog $C$ starts on, pad 2 be the pad frog $B$ starts on, pad 3 be the one pad frog $A$ starts on and pad 4 be the initially empty pad. We'll first show that at least 6 moves will be needed.

Let's present the positions of the frogs with letter arrangements(eg. the initial positions are $CBAO$ , with the letter $O$ noting the empty pad.

Now, moving frog $B$ to pad 3 will take at least one move and moving frog $A$ to pad 2 will take at least one move. As frog $C$ can't go from pad 1 to pad 4 with only one move, moving frog $C$ will take at least two moves. These will take at least 4 moves total.

In addition, in the first move, either frog $A$ or frog $B$ must be moved to pad 4 as it's the only empty pad and frog $C$ can't be moved. Now we know at least 5 moves will be taken.

Finally, if frog $C$ is moved at least three times, at least 6 moves are now used. If frog $C$ is only moved twice, let's prove that either frog $A$ or frog $B$ will be moved onto pad 1, which would take a sixth move. Let's assume frog $A$ and frog $B$ are never moved onto pad 1. In that case, we have a situation where frog $C$ is on pad 2 or 3 and frogs $A$ and $B$ on pad 2 and 4 in either order, ie. $OCAB$ , $OACB$ , $OCBA$ OR $OBCA$ .At some point, the frog on pad 4 has to be moved (because neither frog $A$ nor $B$ is on pad 4 in the end). This is impossible before frog $C$ or the other frog on pad 2 or 3 is moved onto pad 1. If it was frog $C$ , it would now have been moved twice, and it would have to be moved at least once more as it's not on pad 4 where it will be in the end. This means, the other frog , which is either $A$ or $B$ , has to be moved onto pad 1 and we have proven by contradiction that a move will be taken to move either frog $A$ or frog $B$ on pad 1.

Now, let's prove we have a solution with 6 moves:

We find $CBAO \mapsto CBOA \mapsto OBCA \mapsto BOCA \mapsto BACO \mapsto BAOC \mapsto OABC$ . This is a solution with 6 moves. Thus, the answer is $6$ .

My initial solution from July 29, 2017: Let = denote the blank lilypad. The starting configuration is: CBA= The following 6 steps get to the final position of =ABC:

1. C=AB
2. =CAB
3. AC=B
4. ACB=
5. A=BC
6. =ABC

Updated solution August 2, 2017: Per Calvin's suggestion, I'm adding a proof that 6 is the minimum by considering all possible states after 3 "useful" moves and then showing that at least 3 more steps are needed to get to the desired final state. Things to notice: (1) at step 1, there are only 2 moves (only A or B can move), (2) at each subsequent step there are only 2 "useful" moves because there are at most 3 moves (A, B, or C can move) but 1 of these moves undoes the move from the previous step. Thus, there are at most 8 possible states after 3 "useful" moves. With the same notation above and the minimum path bolded and parenthesis to indicate branch paths, the possible states after each useful move are:

1. CB=A or C=AB
2. (C=BA or =BCA) or ( =CAB or CA=B)
3. ((=CBA or CAB=) or (B=CA)) or (( AC=B ) or (CAB= or =ACB)) - Note that 2 of the 8 states are missing because when the empty pad is on an end, there is only 2 possible moves and so only 1 of them is "useful". Also, 1 state, CAB=, is duplicated so there are only 5 cases.

Next, notice that a frog can only move either 1 or 2 spaces per step. Let's count how many steps are needed to get to the final state of =ABC for each of the 5 cases after step 3.

1. For =CBA, A and C both need to move 2 spaces so we need at least 2 more steps, but from this configuration neither A nor C can do this on the next step so we need at least 3 more steps.
2. For CAB=, C needs to move 3 spaces, so we need at least 2 more steps, but from this configuration C cannot move on the next step so we again need at least 3 more steps.
3. For B=CA, A, B, and C each need to move so we need at least 3 more steps.
4. For AC=B , again A, B, and C each need to move so at least 3 more steps.
5. For CAB=, this is a duplicate of #2.
6. For =ACB, B and C both need to move exactly 1 space so we need at least 2 more steps, but from this configuration, neither can move exactly 1 space on the next step so we need at least 3 more steps.

Having exhausted all possible cases, the minimum number of moves is 6.

CBA_ -> C AB -> _CAB -> AC B -> ACB_ -> A_BC -> _ABC

All jumps over another letter to the right must be done by a "higher" ranked letter and all jumps over another letter to the left must be done by a "lower" ranked letter.

Initial position= CBAO where O is empty Lily pad 1.CBOA 2.OBCA 3.BOCA 4.BACO 5.BAOC 6.OABC