Not 1803 Sangaku Problem
A green circle of radius 5 , a yellow circle, and a blue square are inscribed without overlap inside a circle of radius 2 0 .
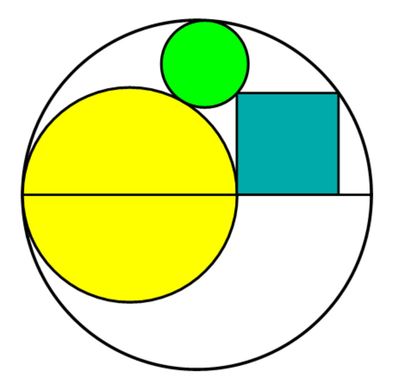
The diameter of the largest circle and of the yellow circle are colinear with the bottom side of the blue square. The upper vertices of the blue square lies on the circumferences of the green circle and the largest circle. The green circle is not tangent to any side of the blue square. All the circles are tangent to each other.
Find the area of the blue square.
The answer is 144.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
nice approach sir!
Terrific solution, Vreken. You've gone over what I call the "hiccups" of this problem, i.e., it undergoes transistions as the yellow circle change in y . The original 1803 sangaku was considerably smoother.
Log in to reply
Thank you! I was hoping to find a simpler solution but could not.
This diagram really captures the general case, particularly the fact that QO is not necessarily perpendicular to the diameter of the large semicircle (which would make the solution much easier). Thank you for your effort and insight, @David Vreken .
Keeping the spirit of 1803 Sangaku problem, the right problem should be to prove that line joining centers of two circles ( 5 and 20 cm radii ) is perpendicular to horizontal diameter of the 20 cm circle. Remaining problem of area of square is very simple one. However, in brilliant format, it is just not possible to address the question.
You've missed y=10, b=h=5*2^(3/2), so the green circle would be tangent to the vertical side of the square.
Log in to reply
The question states that "the green circle is not tangent to any side of the blue square".
Log in to reply
It states that they do not overlap, but you've considered that case. In fact there are 4 cases not counting symmetric and zero cases: 1 solution + 1 tangent+2 overlapping. Here are 3 of them:
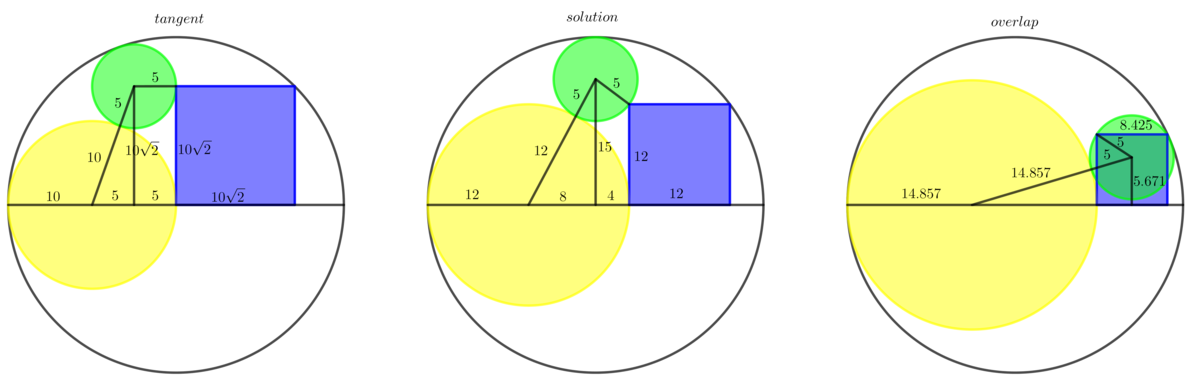
Log in to reply
@Iliya Hristov – The equation − y 2 + 2 0 y + 1 0 0 = 4 ( − y 2 + 1 5 y ) + ( 4 y − 4 0 ) p + y 2 − 2 0 y + 1 0 0 in my solution also has a solution of y = 1 0 , but I did not write this out as since this is the tangent case case and can be rejected by the parameters of the question.
The only way i found to solve to problem is to assume that A (the center of the green circle) is on the perpendiculare bisector of the diameter of the biggest circle.
Then we use the pythagorean theorem to calculate AI, since we know that AJ=15 and JI=20 and we find that AI=25:
- Next, AJ is parallel do EC, then the triangles AJI and EIC are similar
- We denote FG as R and EC as c
- we write : E C A J = I C I J <=> c 1 5 = 4 0 − 2 R 2 0
- This gives us this equation : R= 3 6 0 − 2 c
- The product of chords in a circle gives us this second equation : c²=(2R+c)(40-2R-c)
- We use substitution de solve the system and find c=12 -The area of the square is c²=12²=144
This is one of those cases where a good or lucky hunch leads to a reasonably straightforward solution.
Log in to reply
Professor Mendrin, i tried to use cosine law and other stuff but the algebra was getting extreme...is there a way? Thank you.
It certainly looks like the segment between center of the green circle and the large circle is perpendicular to the diameter on which the base of the square lies. But I wasn't able to prove that.
I solved it by saying that the length of an edge of the square, plus the radius of the small circle, plus the radius of the small circle times the sine of the angle to the corner of the square all had to add up to the radius of the large circle.
Log in to reply
To G Silb,
If you can give your solution, Thanks .
To Valentin Duringer,
Please clear, AG=R+5.
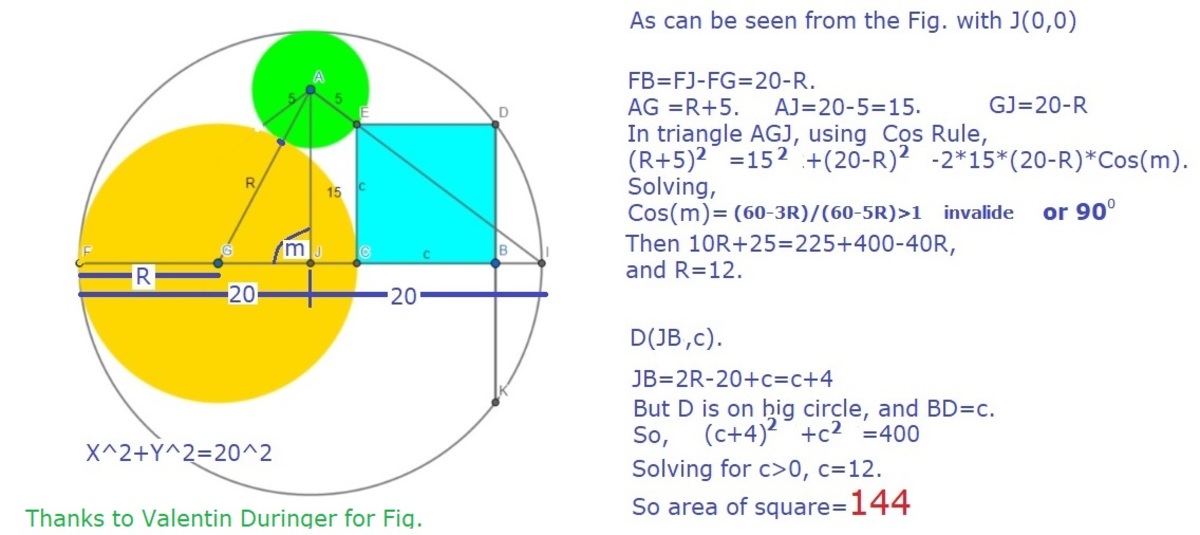
Please add,
Cos(m)=(60-3R)(60-5R)>1 invalid,
O
R
=
0
,
m
=
90 degrees.
A
(
(
0
,
1
5
)
,
E
(
4
,
1
2
)
,
S
o
A
E
=
(
0
−
4
)
2
+
(
1
2
−
1
5
)
2
=
5
=
r
a
d
i
u
s
o
f
g
r
e
e
n
c
i
r
c
l
e
,
O
K
.
Log in to reply
Beautifully done, @Niranjan Khanderia ! Many thanks!
Solving the cosine rule gets me the inverse of what you have there, could somebody show me why I'm wrong? I'm sure I am but I've been trying for a while and I can't see it
Log in to reply
Without seeing your work, it is not possible to know what is not correct.
You’re right.
AI^2=15^2+20^2 => AI=25 => EI=AI-5=20 => c/15=20/25 => c=12
There is one more assumption without a proof, that the points A, E and I lie on a straight line.
I solved it by drawing it on graph paper on iPad using ipencil with all the conditions of the problem.

Let y be the radius of the yellow circle and b be the side of the square, and label the diagram (not drawn to scale) as follows:
Then O B = 2 0 as the radius of the big circle, A B = b as the side of the square, and O A = V D + D A − V O = 2 y + b − 2 0 . By the Pythagorean Theorem on △ O A B , ( 2 y + b − 2 0 ) 2 + b 2 = 4 0 0 , which rearranges to b = − y 2 + 2 0 y + 1 0 0 − y + 1 0 .
Also, P Q = P R + R Q = y + 5 , O Q = O U − Q U = 2 0 − 5 = 1 5 , and P O = V O − V P = 2 0 − y . By the law of cosines on △ Q P O , cos ∠ Q P O = ( 2 0 − y ) ( y + 5 ) ( 2 0 − y ) 2 + ( y + 5 ) 2 − 1 5 2 . Letting k = P T and h = Q T , on △ Q P T , cos ∠ Q P O = y + 5 k and k 2 + h 2 = ( y + 5 ) 2 . These three equations simplify to k = 2 0 − y y 2 − 1 5 y + 1 0 0 and h = 2 0 − y 2 0 − y 2 + 1 5 y .
Also, Q C = 5 as the radius of the green circle, Q S = Q T − S T = h − b , and S C = T D = P D − P T = y − k . By the Pythagorean Theorem on △ Q S C , ( y − k ) 2 + ( h − b ) 2 = 2 5 , which after substituting the above values, ( y − 2 0 − y y 2 − 1 5 y + 1 0 0 ) 2 + ( 2 0 − y 2 0 − y 2 + 1 5 y − ( − y 2 + 2 0 y + 1 0 0 − y + 1 0 ) ) 2 = 2 5 .
If p = − y 2 + 1 5 y and q = − y 2 + 2 0 y + 1 0 0 , the above equation becomes ( y − 2 0 − y y 2 − 1 5 y + 1 0 0 ) 2 + ( 2 0 − y 2 0 p − ( q − y + 1 0 ) ) 2 = 2 5 . Solving this for q and simplifying gives q = y − 2 0 − 2 0 p ± 2 p ( y − 1 0 ) + y − 1 0 , which means either q = 2 p + y − 1 0 or q = y − 2 0 − 2 p y + y − 1 0 . If q = 2 p + y − 1 0 , then q 2 = 4 p 2 + ( 4 y − 4 0 ) p + y 2 − 2 0 y + 1 0 0 , or − y 2 + 2 0 y + 1 0 0 = 4 ( − y 2 + 1 5 y ) + ( 4 y − 4 0 ) p + y 2 − 2 0 y + 1 0 0 . Solving this for p and simplifying gives p = 2 1 y , which means p 2 = 4 1 y 2 , or − y 2 + 1 5 y = 4 1 y 2 , which simplifies to y ( y − 1 2 ) = 0 , so that y = 1 2 for y > 0 . If q = y − 2 0 − 2 p y + y − 1 0 , the same steps above will lead to y ≈ 1 4 . 8 5 7 , which would make the green circle overlap the square. Therefore, y = 1 2 .
If y = 1 2 , then b = − y 2 + 2 0 y + 1 0 0 − y + 1 0 = − 1 2 2 + 2 0 ⋅ 1 2 + 1 0 0 − 1 2 + 1 0 = 1 2 , and the area of the square is b 2 = 1 2 2 = 1 4 4 .