Not enough information!
If x and y are real numbers such that x + y = 7 and x 3 + y 3 = 1 3 3 , find the value of x y .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
47 solutions
FYI, x and y are 2 and 5.
Log in to reply
Why did people downvote this comment? He's right...
Log in to reply
Jealousy I guess
Hmm... yes. Why did this happen?
Exactly it's 2 and 5
obviously and of course the product is 10.
replying 6 years and 9 months late(Nice) to say: how did you find the solution? is it just a guess or can it be proven algebraically
Correct :D
You should have used the identity: ( x + y ) 3 = x 3 + y 3 + 3 x y ( x + y )
How you all know x3+y3 is equal to (x+y)(x2+y2-xy)? Please teach me.
Log in to reply
because x 3 + y 3 is a sum of perfect cubes. As such, it has the special factorization of x 3 + y 3 = ( x + y ) ( x 2 − x y + y 2 )
Log in to reply
so what is the xy there? in (x2-XY+y2)? i'm confused. please explain it to me. Thanks :)
Log in to reply
@Kat Auditor – It's just the formula; it's typically taught in beginning algebra classes. If you go and multiply it out, you see that the xy term is needed to cancel the x2y and y2x terms. If you need proof, google sum of cubes.
That was the missing step/explanation. Thank you.
i think he use special products
where do you get 49 and how it formed 30=3xy and 10=xy?
Log in to reply
x + y = 7 , therefore ( x + y ) 2 =49.
By doing some rearranging of the equation you get those equations.
I guess I should start writing solutions to level 1 problems. 89 upvotes for nothing .-.
Log in to reply
:P 109 upvotes.
222 now. :P :P
Log in to reply
This is cancer lel. People seem to upvote a solution if they've implied a similar method, not because it's elegant.
Log in to reply
@Kunal Verma – 246 on this one and 353 over here . :P About a third of my total upvotes from these two questions only.
Log in to reply
@Sharky Kesa – 250 on this one and 420 upvotes there. I think I broke the record on that prob!
but where did -xy came from? i get that x+y is taken as common.
correct answer
Very well.
I don't understand how you got (x^2+y^2+2xy-3xy) from (x^2+y^2-xy).
x^3 + y^3 = (x + y)^3 - 3xy (x + y) 133 = 7^3 - 3xy (7) 133 = 343 - 21xy 21xy = 343 - 133 xy = 210/21 xy = 10
The solution is quite easy..
given that x + y = 7 2 + 5 =7 x^3 + y^3 =133 2^3 + 5^3=133 (x)(y)=? (2)(5)=10
brilliant answer
unfortunately I added negative sign to 10
Wait x^3 + y^3 = (x+y) ( x^2 -xy +y^2) = 133
x + y = 7 ⇒ ( x + y ) 3 = 7 3 ⇒ x 3 + 3 x 2 y + 3 x y 2 + y 3 = 3 4 3 We know that x 3 + y 3 = 1 3 3 So substituting ⇒ 3 x 2 y + 3 x y 2 = 2 1 0 Take out the 3 and factorise ⇒ ( x + y ) x y = 7 0 ⇒ x y = 1 0
solved in the same way : )
Even I solved in the same way.....
one just have to remember the correct expansion formula
Superb explanation
this is much clear , this is simpler than other ways
your ans seems be a more valid solution than others. thanks
Before working with simultaneous equations and substitution, which is somewhat time-consuming, I take no shame in having entertained the idea of a shortcut (with the assumption that x and y would take natural values): the only cubic numbers below 133 are 1, 8, 27, 64 and 125. I then noticed that 125 + 8 = 133. Therefore because x^3 and y^3 are 8 and 125 (in any order), xy = 2 * 5 = 10.
What I did also.
This is how I did it. Well done sir.
(
x
+
y
)
3
=
x
3
+
y
3
+
3
x
y
(
x
+
y
)
and given that (x+y) = 7
so,
(
7
)
3
=
1
3
3
+
3
x
y
(
7
)
2
1
0
=
2
1
x
y
x
y
=
1
0
We know,
(x+y)^3 = x^3 + y^3 + 3xy(x+y)
or, 7^3 = 133 + 3xy * 7
or, 343-133 = 21xy
or, 210 = 21xy
or, xy = 10
( x + y ) 3 = 7 3
⇒ ( x 2 + 2 x y + y 2 ) ( x + y ) = 3 4 3
⇒ x 3 + 2 x 2 y + y 2 x + x 2 y + 2 x y 2 + y 3 = 3 4 3
⇒ x 3 + y 3 + x y ( 2 x + y + x + 2 y ) = 3 4 3
⇒ ( x 3 + y 3 ) + ( x y ) ( 3 x + 3 y ) = 3 4 3
⇒ ( x 3 + y 3 ) + ( x y ) 3 ( x + y ) = 3 4 3
⇒ ( 1 3 3 ) + ( x y ) 3 ( 7 ) = 3 4 3
⇒ x y = ( 3 ) ( 7 ) 3 4 3 − 1 3 3
⇒ x y = 1 0
( x + y ) 3 7 3 3 4 3 2 1 0 x y = x 3 + y 3 + 3 x y ( x + y ) = 1 3 3 + 3 x y ( 7 ) = 1 3 3 + 2 1 x y = 2 1 x y = 1 0
both X, Y <6, as X+Y=7, & x^3 or Y^3 beyond 5 will make X^3+Y^3>133, Now only pair of numbers less than 6 which add up to 7 are 3,4 or 5,2... now only 5,2 pair satisfies the criteria for both the equations
Incase not remembering formula...Just assume and test...1+6=7 or 2+5=7 or 3+4=7...you get it fast...
x+y=7 x^3+y^3=133 〖(x+y)〗^3=x^3+3x^2 y+3〖xy〗^2+y^3=7^3=343 3xy(x+y)=343-133=210 7 3 xy=210 21xy=210 xy=10
( x + y ) 3 = x 3 + y 3 + 3 x y ( x + y )
So,
x 3 + y 3 = ( x + y ) 3 - 3 x y ( x + y )
1 3 3 = 7 3 - 3 x y ( 7 )
1 3 3 = 3 4 3 - 2 1 x y
2 1 x y = 2 1 0
x y = 1 0
X + Y = 7 X³ + Y³ = 133 X³ + Y³ = 125 + 8 X³ + Y³ = 5³ + 2² X³ = 5³ Y³ = 2³ X = 5 and Y = 2
Dude I just tried with 1&6 2&5 Tadaaaa I got it
x+y = 7
(x+y)³ = 7³
x³ + y³ + 3(x+y)(xy) = 343
It admitting also x³+y³ = 133
133 + 3(7)(xy) = 343
3(7)(xy) = 343 - 133
21xy = 210
xy = 10
Used trial and error. So what 2 numbers make 7. 4+3, 5+ 2, 6+1 or 7+0. Tried 4+3, gave me 98 when put into x^3+y^3. Tried 5+2 and gave me 133. Therefore xy=10
( x + y ) 3 = x 3 + y 3 + 3 x 2 y + 3 x y 2
x 3 + y 3 = ( x + y ) 3 − ( 3 x 2 y + 3 x y 2 )
1 3 3 = 7 3 − ( 3 x 2 y + 3 x y 2 )
1 3 3 = 3 4 3 − 3 x y ( x + y )
3 x y ( x + y ) = 2 1 0
x y ( x + y ) = 7 0
7 x y = 7 0
x y = 1 0
(x+y)^3 = x^3+y^3+3xy(x+y) Hence xy = ([(x+y)^3-(x^3+y^3)]/3xy) Hence xy = 10
For those not as mathematically inclined, there is a simple guess and check. Where x+y=7 and x^3+y^3=133, there are only so many options out there. After enough guessing, we can conclude 5+2=7, and 5^3(which is 125) and 2^3(which is 8) equals 133.
I knew the maths, but it was gonna take too long doing all the calculations. So all I did was possibility and elimination. It's faster:
x + y = 7
This means that there will be only 1 combination numbers for this first equation: 4 + 3 5 + 2 6 + 1
So, if x^3 + y^3 = 133, if I insert the three possibilities into the equation, it should give me 133. So...
(4^3) + (3^3) = 91 ---> Not it
(5^3) + (2^3) = 133 ---> Here we go :)
5x2 = 10
Et voilà
As I was careful to indicate in my first post on this site, I'm no expert mathematician. This was how I approached the problem and arrived at the correct answer: Given that x+y = 7, my task was to find two numerals which, when added, would total 7. The sum of the cubes of these same two numerals must also yield 133. My options were: 0+7=7; 1+6=7; 2+5=7; 3+4=7; 4+3=7; 5+2=7; 6+1=7;or 7+0=7. First, I eliminated 0+7 and 1+6 because the sum of their cubes (0 0 0+7 7 7) did not total 133. My next option was 2+5 which, when their cubes were added, gave the following: (2 2 2) + (5 5 5) = 8+125 = 133. This satisfied formulae 1 and 2: x+y = 2+5 = 7; and x^3+y^3 = 133. Finally, x y = 2 5 = 10. ANSWER: 10. NB I did not find it necessary to explore the remaining five options, because the answer was evident at my third option. I could, of course, have stopped counting options after 3+4, since anything after that is a retrograde repetition of earlier options.
There are some people who don't know exactly how to do some of the formulas So if you are a beginner you can just use system of elimination We all know that there are different numbers that can come together to make 7 like 4+3 or 6+1 or 5+2 and more so if you take the time you can obviously solve it just conduct the formula with each pair of numbers and you will realize 5+2 make the best answer so then just Multiply it by 2 and then you will Get 10 But Sharky Kesa did a great job By the way I am actually thirteen I just set it like this because I didn't know the age limit
x3+y3= {x+y}3 - 3xy(x+y}=7x7x7 - 3xy x 7 =343 - 21xy 133 - 343 = - 21xy -210 = -21xy Then xy = -210/-21 = 10
(x+y)³=7³ - Taking the first equation and ^3 the both sides we have: x³+3x²y+3xy²+y³=343 Now we make:
x³+3x²y+3xy²+ y³= 343
-x³ - y³= -133
0x³+3x²y+3xy²+0y³= 210
so:
3xy(x+y) = 210 but x+y = 7
what lead us to:
xy = 210/ (3*7) xy = 10
x + y = 7
(x + y)³ = 343
(x³ + y³) + 3x²y + 3xy² = 343
133 + 3x²y + 3xy² = 343
3x²y + 3xy² = 210
x²y + xy² = 70
xy (x + y) = 70
7xy = 70
xy = 10
well, i just paired up the nos. that added to 7 and then checked them with the cubes
x^3 + y^3 = (x + y)^3 - 3xy(x + y) = 133
-> 7^3 - 3xy.7 = 133 #plug (x + y) = 7
-> 343 - 21xy = 133
-> - 21xy = 133 - 343 = - 210
-> xy = 10
(x+y)^3 =x^(3 )+3x^2 y+3xy^2+y^3
7^3 =x^(3 )+y^3 +3x^2 y+3xy^2
343 =133+3xy(x+y)
343 =133+3xy(7)
343-133=21xy
210 =21xy
∴xy=10
I think I did it the dumb way and just picked a number hence 5 and 2 and put it into the equation getting 5^3+2^3 which equals 133 lol.
I just manually tried it. first by considering a pair of 4&3 but since cube of 4&3 equals 64 + 27=91 so then I tried for 5&2 i.e. 125+8=133 which proved to be correct
We have the following system,
x + y = 7
x ³ + y ³ = 1 3 3
Elevating in both sides x + y = 7 , we have:
( x + y ) ³ = 7 ³
x ³ + 3 x y ² + 3 x ² y + y ³ = 7 ³
Now The System is:
x ³ + 3 x y ² + 3 x ² y + y ³ = 3 4 3 ³ (1)
x ³ + y ³ = 1 3 3 (2)
Subtracting (1) and (2), we have:
3 x y ² + 3 x ² y = 2 1 0
3 x y ( x + y ) = 2 1 0
We know that x + y = 7 , So:
3 x y ∗ 7 = 2 1 0
x y = 2 1 0 / 2 1
x y = 1 0
(x+y)(x^2-xy+y^2)=133
7(x^2-xy+y^2)=133
x^2+2xy+y^2=49
x^2+y^2=49-2xy
7(49-3xy)=133
49-3xy=19
xy=10
(x +y)^3 - 3xy (x+y) = x^3 +y^3 or, 7^3- 3.7xy = 133 or, xy = 343- 133 = 10.
taking x=7-y and substituting in equ 2 we get a quadratic equ solving that in x+y=7 we get the values for x and y as 5 and 2 so ans is 10
x^3 + y^3 = (x+y) [(x+y)^2 - 3xy] 133 = 7 (7^2 - 3xy) 133 = 7 (49 - 3xy) 133/7 = (49 - 3xy) 19 = 49 - 3xy 3xy = 49 - 19 3xy = 30 xy = 10
x^3 + y^3 = 133 then (x + y) (x^2 + y^2 -xy ) = 133 since x+y = 7 then 7( x^2 + y^2 - xy ) 133 7( (x+y)2 - 3xy ) =133 7( 49 -3xy ) = 133 343 + 7xy = 133 -21xy = -210 xy = 10
x^3 + y^3 + 3 x y (x + y) = (x + y)^3
=> 133 + 3 x y (7) = 7^3
=> 19 + 3 x y = 49
=> x y = 10
x^3+y^3= 133 =(x+y)(x^2-xy+y^2)= 7(x^2-xy+y^2) x^2-xy+y^2= 133/7= 19 //+3xy x^2+2xy+y^2= (x+y)^2=7^2= 49=19+3xy 3xy=30 xy=10
6 6 6* = 256 so a number must be less than six...which means automatically 5...and 5 5 5 = 125 and 2 2 2= 8 and their sum 133 and 5+2 = 7 5*2 =10
(x+y)^{ 3 }=(x^{ 3 }+y^{ 3 })+3x^{ 2 }y+3xy^{ 2 }\ (7)^{ 3 }=(133)+3xy(x+y)\ 343=133+3xy(7)\ 210=21xy\ xy=210/21\ xy=10
x + y (5 + 2 or 2 + 5) = 7. xy = 10
(x+y)^3 = x^3 + y^3 + 3x^2 y + 3x y^2
7^3=133+ 3xy(x+y)
343-133=3xy(7)
xy=210/21
xy=10
given x^3+y^3=133; x+y=7 we know the formula (x+y)^3=x^3+y^3+3xy(x+y) substitute the values 7^3=133+3(7)xy on solving we get 10=xy
We know that (x+y)^3=x^3+y^3. 343=133+21xy. 21xy=210,so xy=10.
Using Formula, x^3 + y^3 = (x+y)(x^2 + y^2 - xy) x^2 + y^2 - xy = 19 ....(1) Using (x+y)^2 = x^2 + y^2 + 2xy x^2 + y^2 + 2xy = 49 ....(2) By Solving (1) & (2) We can get xy = 10
x^3+y^3=(x+y)^3-exy(x+y)=133; -21xy=-210;xy=10
Could you use L A T E X instead?
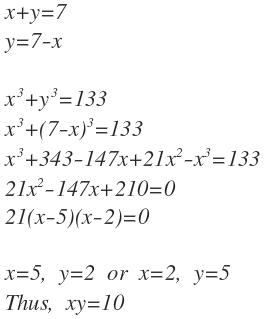
x 3 + y 3 = ( x + y ) ( x 2 + y 2 − x y )
1 3 3 = 7 ( x 2 + y 2 + 2 x y − 3 x y )
1 9 = ( x + y ) 2 − 3 x y
1 9 = 4 9 − 3 x y
3 0 = 3 x y
1 0 = x y