Not related to the Umbrella Corporation
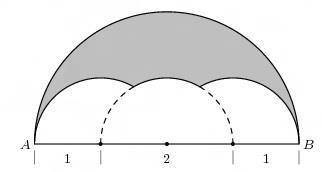If the area of the shaded region equals
7
x
−
cos
x
, what is the value of
x
π
?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yay! Correct! Doesn't this look like an umbrella?
Log in to reply
Yes, it does and it reminded me of the recent Hong Kong Umbrella Revolution. Sorry to be political.
Log in to reply
I solved it using integration.........
Log in to reply
@Rajat Kharbanda – Yes, post solution. I am not very fond of calculus and integration.
Lol! Umbrella Corp . haha
truly a fantastic solution
Sir , how did u get that the 2 parts of circle with radius 1cm occupies 1/3 area of the original circle i.e. third line of ur answer and also that part of circle that occupies 1/6 area of another circle(i.e. fourth line) ??
Log in to reply
I have changed the figure. 3 π and 6 π indicate the one-third and one-sixth of a radius-1 circle respectively. Hope it helps.
Total required area = 2*Pink area=All area -2( green+blue+red) areas.
R
e
q
u
i
r
e
d
a
r
e
a
=
2
∗
π
−
2
∗
(
2
1
∗
6
π
−
4
3
−
2
1
∗
3
2
∗
π
)
=
{
6
7
∗
π
−
2
3
}
=
6
7
∗
π
−
C
o
s
6
π
=
X
−
C
o
s
X
⟹
6
π
=
X
.
.
S
o
X
π
=
6
.
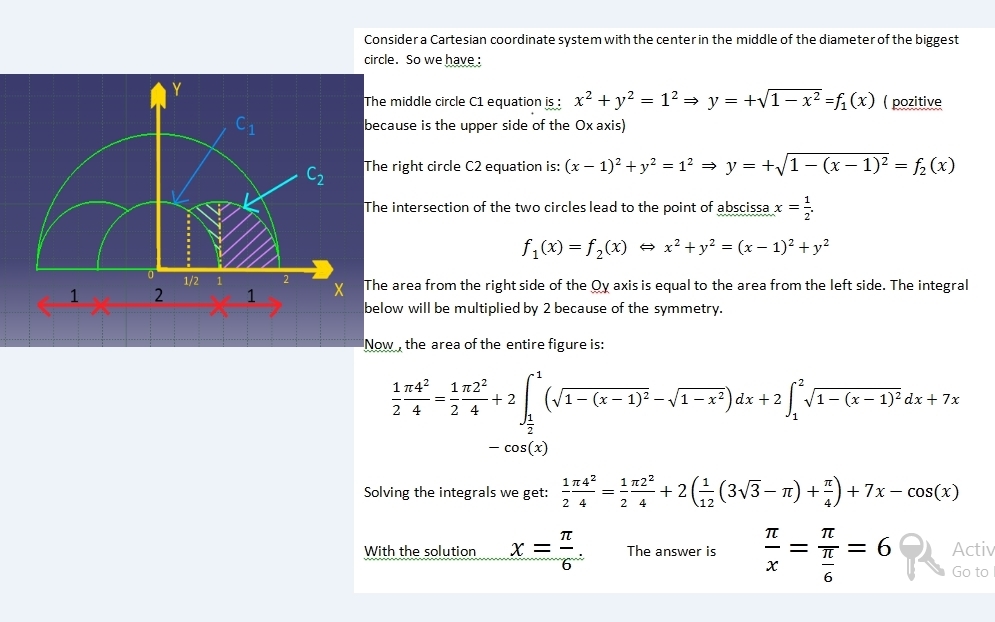
The area of the shaded region
A = Area of the radius-2 semicircle − 2 × Area of 3 1 of radius-1 circle − Area of 6 1 of radius-1 circle − 2 × Area of side length-1 equilateral triangle = 2 1 π ( 2 2 ) − 2 × 3 1 π − 6 1 π − 2 × 2 1 ( 1 ) ( 2 3 ) = ( 2 − 3 2 − 6 1 ) π − 2 3 = 6 7 π − 2 3 = 6 7 π − cos ( 6 π )
⇒ x = 6 π ⇒ x π = 6