Not the Deathly Hallows Symbol

Geometry Level 5

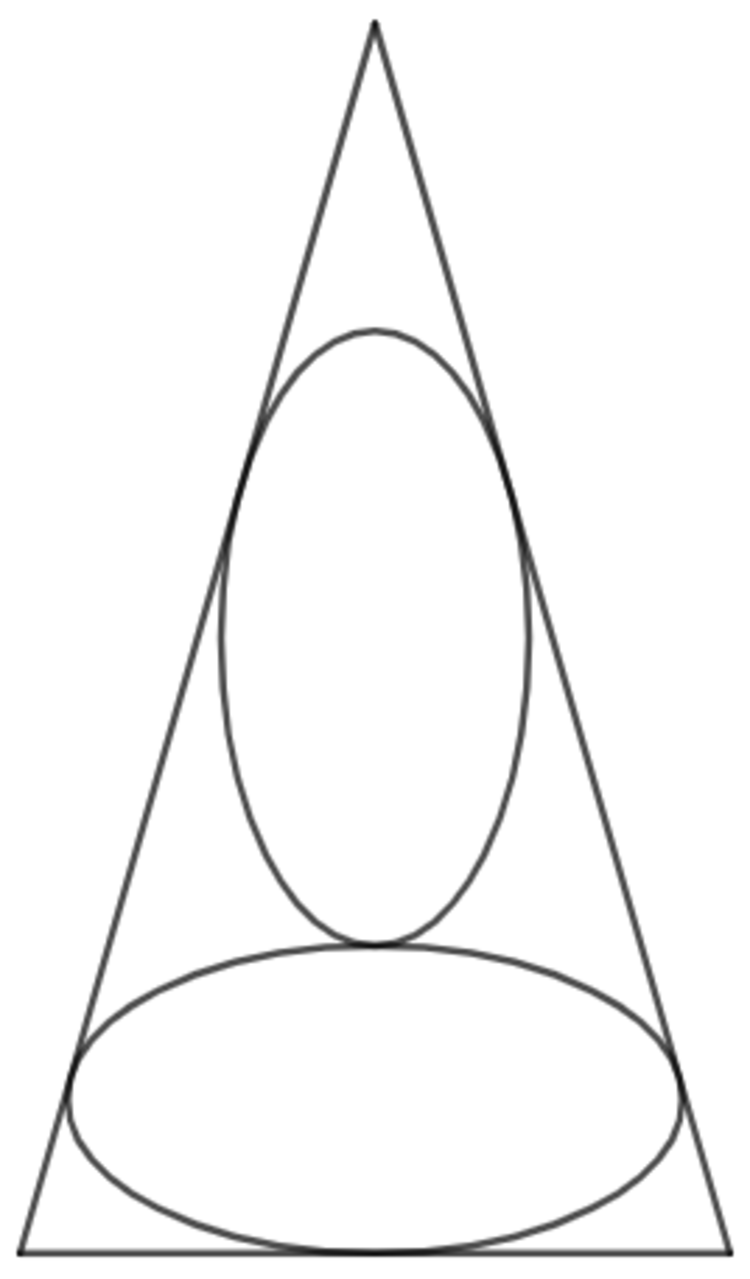
Two adjacent identical ellipses are symmetrically positioned and inscribed inside an isosceles triangle, such that the major and the minor axes are collinear with one of the altitudes. It is known that the length of their minor axis is $2$ . As shown above, one ellipse touches the triangle at two points, whereas another whose major axis is parallel to the base touches at three points. There exists the eccentricity $e > 0$ , such that the vertical altitude (height) of the triangle achieves its minimum value. Input $\lfloor 10^6 e \rfloor$ as your answer.

The answer is 866025.

1 solution

Pi Han Goh
Feb 13, 2021

To compute the eccentricity, all we care about is the ratio between the minor-axis and the major-axis. So, without the loss of generality, we can assume that the minor-axis is 1 (instead of 2), and the major-axis is $a>1$ .

We can plot these ellipses in a Cartesian plane, where the bottom ellipse's center is at the origin. Thus, the equation of the bottom ellipse is

$\frac{x^2}{a^2 } + y^2 = 1 \tag1$

And the equation of the top ellipse is

$x^2 + \frac{(y-a-1)^2}{a^2} = 1 \tag2$

The base of the triangle is part of the straight line $y = -1$ . Also, let $y = mx + c \tag3$ denote the equation of the straight line that passes through the two ellipses on the second quadrant ( $x<0, y>0$ ). So $m >0, c> 0$ .

The plot of the 2 ellipses and the 2 straight lines

Substitute $(3)$ into $(1)$ yields a quadratic equation (in $x$ ), $\dfrac{x^2}{a^2} + (mx + c)^2 = 1.$

And because this straight line is tangent to the ellipse, then its quadratic discriminant must be 0,

$a^2 (a^2 m^2 - c^2 + 1 ) \, =\, 0 \quad \stackrel{a > 1}{\Leftrightarrow} \quad (am)^2 + 1 \, =\, c^2 \tag 4$

Likewise, substitute $(3)$ into $(2)$ , we get another quadratic equation with a discriminant of 0, $2ac - 2a - c^2 + 2c + m^2 - 1 = 0 \tag 5$

Solving for $(4)$ and $(5)$ in terms of $a$ yields $c \, = \, \dfrac{2a^2-a+ 1}{a-1}, \quad m \, =\, \dfrac2{a-1} \sqrt{a^2-a + 1}.$

Thus, the vertical altitude is simply $c + 1 \, =\, \dfrac{2a^2 -a + 1}{a-1} + 1 \, = \, 2 \left( a + \dfrac1{a-1} \right) + 2 = 2\cdot \underbrace{\left( a - 1 + \dfrac1{a-1}\right) }_{\geqslant 2} + 4 \geqslant 2 \cdot2 + 4 = 8$

The penultimate step above follows from the AM-GM inequality . In other words, the longest altitude achieves its minimum value of 8 when $a - 1 = \frac1{a-1} \Leftrightarrow a = 2,$ or when the major-axis of the ellipse is twice the length of the minor-axis.

The eccentricity in question is $e = \sqrt{1 - \frac1{a^2}} = \frac{\sqrt3}2$ . Hence, the answer is $\lfloor 10^6 e \rfloor = \lfloor \num{500000} \sqrt3 \rfloor = \boxed{866025} .$

Footnotes:

Here's a Desmos graph for users to visualize the figure .
When the longest altitude of the triangle achieves its minimum value, the lengths of the triangle has a ratio of $\sqrt{259} : \sqrt{259}: 8 .$

Meaningless goose chase:

I previously mistook "altitude" as "length", and I went into a meaningless goose chase and I couldn't spot my error for over an hour. Nevertheless, if the directive reads:

There exists the eccentricity $e$ , such that the longest $\red{\text{length}}$ of the triangle achieves its minimum value. Input $\lfloor 10^6 e \rfloor$ as your answer.

Then, here's my solution:

Use formula $(1)$ on the values of $18^\circ$ to get the values.

Let us first find the coordinate of the triangle in the bottom-left quadrant of the Cartesian plane, which is simply the intersection point between the straight line $y=m x + c$ and $y = -1$ . Upon substitution, the coordinate is $\left( -\dfrac{a^2}{\sqrt{a^2-a+1}} , -1 \right)$ .

Thus, by Pythagorean theorem , the longest length in question is $\ell := (c + 2)^2 + \left( -\dfrac{a^2}{\sqrt{a^2-a+1}} \right)^2$ . We want to minimize $L := \ell^2 = \left(\dfrac{2a^2 - a + 1}{a-1} + 1\right)^2 + \dfrac{a^4}{a^2-a+1}$

Now, this is where it started getting super tedious!

At its critical point(s), $\frac{dL}{da} = 0$ . Do a bunch of tedious quotient rule , we can gather that $L$ is minimized when $10 a^5 - 41 a^4 + 75 a^3 - 87 a^2 + 55 a - 20= 0 \quad\Rightarrow\quad a \approx 1.92751.$

Do the same working as above to get $\lfloor 10^6 e\rfloor= \lfloor 10^6\cdot 0.854894\rfloor = 854894$ .

Pi Han Goh - 3 months, 4 weeks ago

Haha! I took some time to rephrase my question as best as possible. I meant vertical altitude (with respect to how the diagram was drawn), but I can even ask that. XD

Michael Huang - 3 months, 4 weeks ago

You can ask this:

(Same image) Two adjacent identical ellipses are symmetrically positioned and inscribed inside the triangle, such that the major and the minor axes are collinear with one of the altitudes. As shown above, one ellipse touches the triangle at two points, whereas another whose major axis is parallel to one of the three triangle sides touches at three points.

Can this triangle be an equilateral triangle?

The answer is No .

Pi Han Goh - 3 months, 4 weeks ago

@Pi Han Goh – I leave that for you to ask then as you brought this up. :)

Michael Huang - 3 months, 4 weeks ago

I believe it makes a difference if you choose $a$ or $b$ to be fixed for the question. If you fix $a = 1$ instead of $b = 1$ , then $c = \cfrac{b^2 - b + 2}{1 - b}$ , $m = \cfrac{2\sqrt{b^2 - b + 1}}{1 - b}$ , and the minimum altitude is $2$ when $b = 0$ , making the eccentricity $e = 1$ .

David Vreken - 3 months, 4 weeks ago

I assume you meant $a$ and $b$ are the major-axis and minor-axis of the ellipse, respectively.

If we fix $a = 1$ , then $0<b< 1$ . So how can we obtain $b = 0$ ? Doesn't that mean that the vertical altitude has an infimum value (but no minimum value)?

Pi Han Goh - 3 months, 4 weeks ago

I used the same variables and methods as you are in your solution, except I let $a = 1$ instead of $b = 1$ . You can see the results here: desmos graph

The minimum height occurs when $b = 0$ . Basically, this is when the ellipses degenerate to line segments and these two segments make an upside-down T-shape for a minimum height of $1$ .

David Vreken - 3 months, 4 weeks ago

@David Vreken – Wow, this is incredible. I can't believe I got blindsided by this.

I'm sorry for not taking your previous comment seriously. Now I'm thinking if there's a way to salvage this question....

Pi Han Goh - 3 months, 4 weeks ago

@Pi Han Goh – Oh I see Michael has rectified the question.

Thank you for pointing this out, David.

Pi Han Goh - 3 months, 4 weeks ago

@Pi Han Goh – I did thanks to David. I missed out the small information about the axis lengths, thinking the answer to the problem would be obvious without it, but after reading the comments I realized it isn't.

Michael Huang - 3 months, 4 weeks ago

@Pi Han Goh – You're welcome! The edited question should be fine now.

David Vreken - 3 months, 4 weeks ago

Not the Deathly Hallows Symbol

The answer is 866025.

1 solution

0 pending reports