Not What It Seems

Geometry Level 2

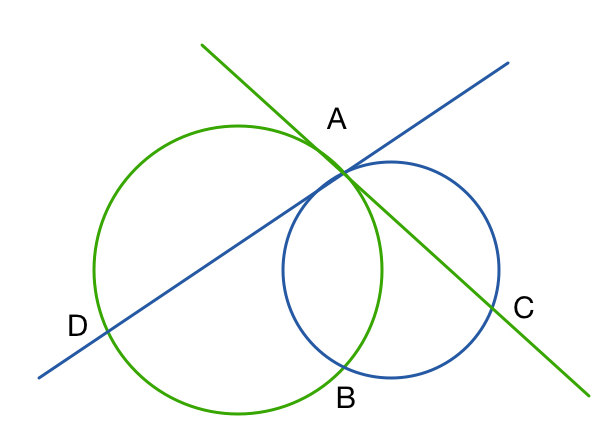
2 circles intersect at $A$ and $B$ .
The tangent to the first circle at $A$ intersects the second circle at $C$ .
The tangent to the second circle at $A$ intersects the first circle at $D$ .
If $B, C, D$ lie on a line, what can we say about $\angle DAC$ ?

\angle DAC = 60 ^ \circ

It is a right angle We do not know anything about

\angle DAC

It is an obtuse angle

3 solutions

Calvin Lin Staff
Oct 30, 2016

By alternate angle segment, $\angle ABD = \angle EAD$ and $\angle CBA = \angle FAC$ . Since $\angle EAD = \angle FAC$ by vertical angles, hence if $CBD$ is a straight line then

$180 ^ \circ = \angle DBA + \angle CBA = \angle DAE + \angle CAF = 2 \angle DAE.$

Hence $\angle DAE = 90^\circ$ and thus $\angle DAC = 90 ^ \circ$ .

Ayush G Rai
Oct 27, 2016

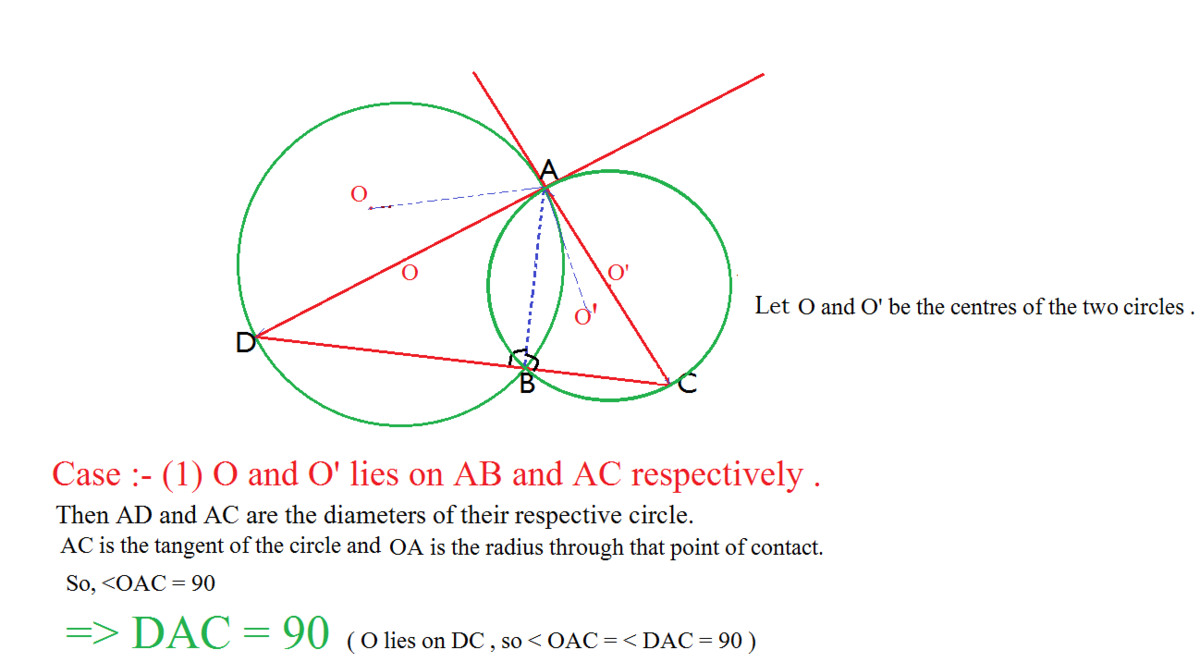
Now let CA be extended till E and DA be extended till F.Now let $\angle EAD=\angle FAC=x.$ [Vertically opp. angles].Join AB. $\angle ABD=\angle ABC=x$ by alternate segment theorem.So,since $B,C,D$ are collinear, $\angle ABD+\angle ABC=180^\circ.$ Therefore $2x=180\Rightarrow x=90$ and $\angle DAC=90.$

The second step is unsubstantiated. Why couldn't $\angle ABD = 150^ \circ, \angle ABC = 30 ^ \circ$ ?

Calvin Lin Staff - 4 years, 7 months ago

But there is a constraint that $B,C,D$ are collinear.How can u say that when $\angle ABC=150^\circ,\angle ABC=30^\circ$ they are collinear?

Ayush G Rai - 4 years, 7 months ago

If $\angle AB {\color{#D61F06} D } = 150^\circ$ and $\angle ABC = 30 ^ \circ$ , then BDC will be collinear, where D, C are on opposite sides of B.

To your claim, if C, B, D are collinear, must we only have $\angle ABD = \angle ABC = 90 ^ \circ$ ?

Calvin Lin Staff - 4 years, 7 months ago

Can you edit your solution to correct the gap?

Calvin Lin Staff - 4 years, 7 months ago

Vishwash Kumar Γξω
Oct 28, 2016

In this case, the proof by contradiction of cases is a very roundabout approach.

It is sufficient to realize, as you did in case 2, that $\angle ABD$ and $\angle ABC$ are equal (by alternate segment theorem and vertical angles). Hence, if they sum up to $180^ \circ$ , then they must be equal.

[Edit: Updated the link from tangent-secant theorem.]

Calvin Lin Staff - 4 years, 7 months ago

I wasn't aware of the theorem. And so I chose to give a complete proof using contradiction method

vishwash kumar - 4 years, 7 months ago

Oh sorry, wrong link. (Too many similar names).

I was referring to the alternate segment theorem / tangent-chord theorem. I think you should be familiar with this.

Calvin Lin Staff - 4 years, 7 months ago

@Calvin Lin – Yeah , now I have read the theorem . Seeing the conversation between you and Ayush . THANKS !😃☺

vishwash kumar - 4 years, 7 months ago

Not What It Seems

3 solutions

0 pending reports