A Weird Cut Of Concentric Circles
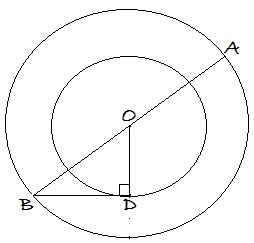
In the figure above, the circles are concentric with centre O . B is a point on the larger circle. D is a point on the smaller circle. B D is joined, provided that B D touches the circle at only one point. Now O B is joined and extended to meet the larger circle at A . Find the distance between points A and D if the radii of the circles are 4 1 3 and 8 units respectively.
Clarification : Concentric circles are circles with a common centre.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I did it the same way!
Why do you write "Find the smallest distance between point A and D" when the length AD is unchanged?
Log in to reply
Its just a simple intentional statement to make the question more complicated
Log in to reply
It is generally best not to unnecessarily complicate the problem.
Imagine if you had to do run a mile before you could submit the answer ...
The simplest method is by the use of coordinate geometry... take the circles with center as the origin then find sin theta and cos theta by trigonometry now the coordinates of A(12,8) by parametric form and B will be (0,-8) using distance formula find AB.
Assume as given in the sketch (but not in the description,) that angle ODB = 90 degrees.
I
n
r
t
.
Δ
O
B
D
B
D
2
=
(
4
1
3
)
2
−
8
2
=
1
6
∗
9
∴
C
o
s
O
B
D
=
4
1
3
1
6
∗
9
=
1
3
3
A
p
p
l
y
i
n
g
C
o
s
R
u
l
e
t
o
Δ
A
B
D
,
A
D
2
=
A
B
2
+
B
D
2
−
2
∗
A
B
∗
B
D
∗
C
o
s
O
B
D
=
4
∗
1
6
∗
1
3
+
1
6
∗
9
−
2
∗
(
8
1
3
)
∗
(
4
∗
3
)
∗
(
1
3
3
)
=
4
0
0
.
Smallest distance between two points is a st. line.
∴
A
D
=
2
0
.
Using the Pythagorean Theorem, BD = sqrt((4 sqrt(13)^2 - 8^2)) = 12. Angle B = arctan(8/12) = 33.69006753. Finally, using the law of cosines, (AD)^2 = (8 sqrt(13)^2 + 12^2 - 2 12 8 sqrt(13) cos(33.69006753) = 400, so AD = 20. Ed Gray
Since 4 1 3 > 8 , the smaller circle has a radius 8 and the larger circle has a radius of 4 1 3 .
Clearly, B D is tangent to the smaller circle at D . Therefore angle B D O = 9 0 ∘ . Then by Pythagorean theorem
B D 2 + O D 2 = O B 2 ⇒ B D = O B 2 − O D 2 = ( 4 1 3 ) 2 − 8 2 = 2 0 8 − 6 4 = 1 4 4 = 1 2
Now extend B D to a point E on the larger circle. Join A D .
Since O B was extended to meet the larger circle at A , A B is the diameter of the larger circle.
Since angle A E B is enclosed in the semicircle, angle A E B is 9 0 ∘ .
In triangle O D B and triangle A E B , angle O B D is common and angle O D B and angle A E B are both 9 0 ∘ . Therefore triangle O D B and triangle A E B are similar. Then,
A B O B = A E O D = B E B D ⇒ 8 1 3 4 1 3 = A E 8 = B E 1 2
Clearly, A E = 1 6 and B E = 2 4 . E D = B E − B D = 1 2 .
Triangle A E D is right angled at E . Therefore
A D = A E 2 + E D 2 = 1 6 2 + 1 2 2 = 2 0 .