Not Your Usual Cylinder - Surface Area
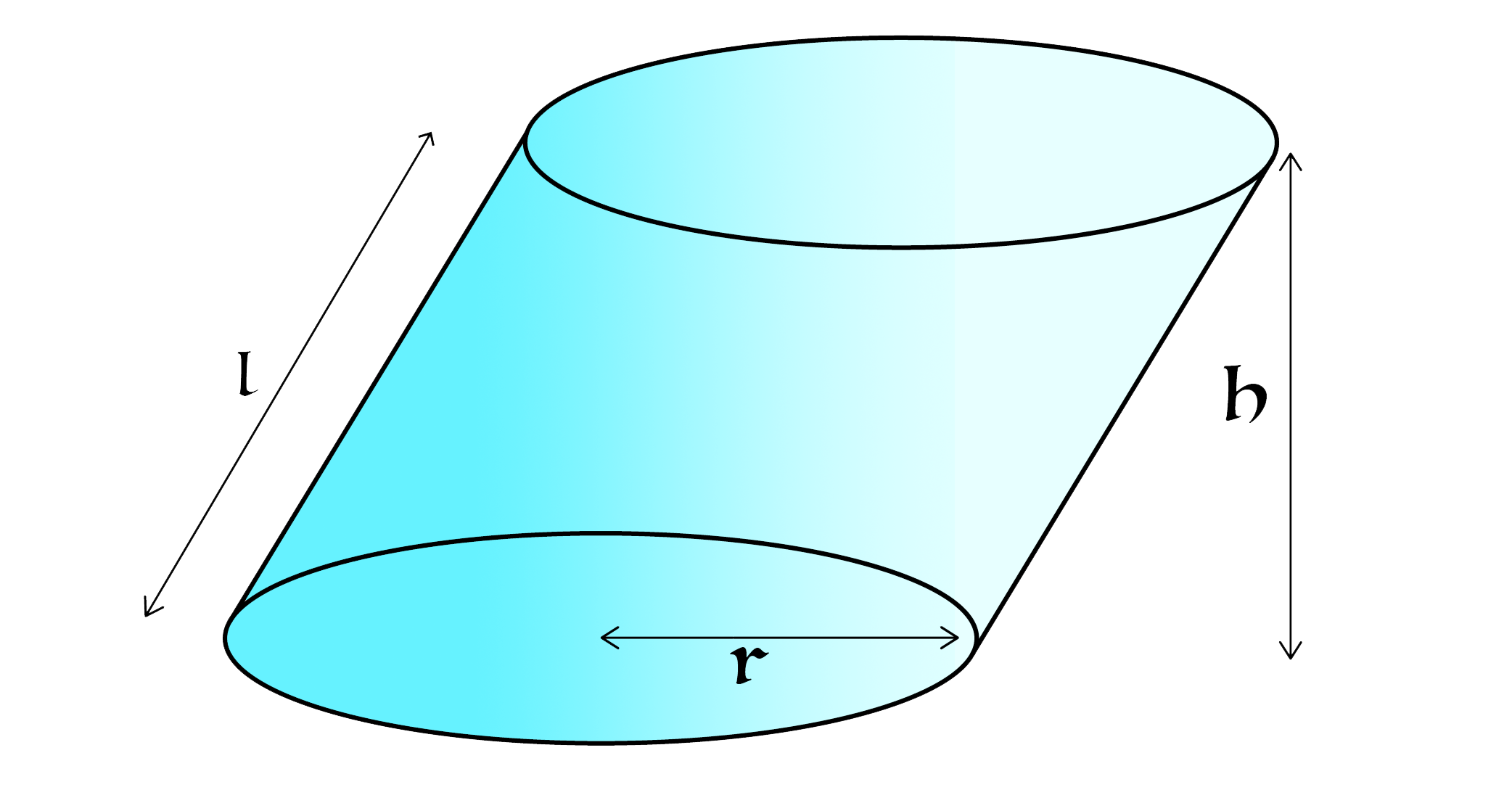
What is the total surface area of the oblique cylinder shown above?
- The flat sides of the cylinder are circular, and are congruent and parallel to each other.
- The slant height of the cylinder is l = 5 .
- The radius of the circular base is r = 2 .
- The perpendicular height of the cylinder is h = 4 .
- The image is not to scale.
State your answer to five significant figures.
Also try: Not Your Usual Cylinder - Volume
The answer is 81.856.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
For those who are familiar with Surface area by Integration , the issues raised here are incorporated into the formula via
S = ∫ a b 2 π y 1 + ( d x d y ) 2 d x
When "cutting the top part to fit below", we end up with an ellipse, and there is currently no way to accurately obtain the perimeter of an ellipse, except in special scenarios.
For those who think that the area must be 2 π r ( r + l ) , let me explain why the "tilted surface area" isn't so easily calculated.
We cannot simply "cut along the seam and unroll it perfectly", because the direction of the surface element causes a significant change in the surface area.
As an explicit example, consider the "tilted cube" with a base of ( 0 / 1 , 0 / 1 , 0 ) and a top of ( 1 / 2 , 0 / 1 , 1 ) (translated one unit to the right and one unit up).
The surface area of the southern face is a rhombus of base 1 and height 1, so it has area 1. The surface are of the eastern face is a rectangle of base 1 and (slant) length 2 , so it has area 2 . The fact that these values are unequal, shows how crucial the "tangent direction" at a point is, in terms of determining the resultant area. Unfortunately, not tangent direction yields the same "increase in area".
For those who think that the area must be 2 π r ( r + l ) , let me explain why the "tilted surface area" isn't so easily calculated. We cannot simply "cut along the seam and unroll it perfectly", because the (normal) direction of the surface element contributes a varying factor in the change to the surface area.
As an explicit example, consider the "tilted cube" with a base of ( 0 / 1 , 0 / 1 , 0 ) and a top of ( 1 / 2 , 0 / 1 , 1 ) (translated one unit to the right and one unit up).
The surface area of the southern face is a rhombus of base 1 and height 1, so it has area 1. The surface are of the eastern face is a rectangle of base 1 and (slant) length 2 , so it has area 2 . The fact that these values are unequal, shows how crucial the "normal direction of the area element" at a point is, in terms of determining the resultant area, and we see that this changes with the direction.
Looking at the formla for surface area, we have to properly account for the 1 + ( d x d y ) 2 , where d z d y represents the "movement in the normal direction". This is why in the south face, when the "movement in the normal direction = 0", the area is a multiplied by 1 + 0 2 = 1 . Whereas, in the east face, where "movement in the normal direction =1", the area is multiplied by 1 + 1 2 = 2 .
Log in to reply
I tried an approach using calculus. We can assume that the oblique cylinder is formed by stacking up very thin coins leaving a small space.
 Image
Image
So I considered an element d x at a distance x along l from the base. Since the element is very small we can assume that its surface area is similar to that of cylinder. Then I just summed up all such particles, i.e, integrated and got a different answer. Please could you point out my mistake? The answer is coming equal to what Svatejas was talking about.
Log in to reply
Try this problem . In particular, similar to your argument, am I allowed to say that "Oh, the horizontal area element is L, and I am integrating over a length of π r , hence the area if π r L ?"
Log in to reply
@Calvin Lin – Ooh I missed a fact that the axis is not perpendicular. I'll try to come up with a solution with calculus using polar coordinates. Thanks for the explanation!
Very good prolem
Log in to reply
Thank you :) I hope you learned something new. What I like about this problem is that its seems very simple at first glance, but in fact it requires a great deal of thought.
Log in to reply
Nice one...never thought it would be so complex
For those who are familiar with Surface Area By Integration , the issues raised here are incorporated into the formula via
S = ∫ a b 2 π y 1 + ( d x d y ) 2 d x
When "cutting the top part to fit below", we end up with an ellipse, and there is currently no way to accurately obtain the perimeter of an ellipse, except in special scenarios.
It is very nice problem. It was taught to me by my dad in 10th grade (i had forgotten it). Now i got it back.
It is worth noting that, while the perimeter of an ellipse does not have a closed expression in term of elementary functions, it does in terms of special functions. The total surface area of the slant cylinder is 8 π + 3 2 E ( − 1 6 9 ) where E is the complete elliptic integral of the second kind: E ( α ) = ∫ 0 2 1 π 1 − α sin 2 θ d θ . This special function is readily found in tables, or calculated by mathematical software, giving the answer 8 1 . 5 8 6 .
Check this link
Log in to reply
What does that link tell you? It merely claims, without justification, that that's the formula. Whereas, Pranshu has provided the reasoning and logic behind why the formula is false.
To further convince yourself that this is wrong, think about the limiting case where the oblique cylinder has no height. In this case, we have 2 base circles, and then 2 "rectangles with semicircles attached / removed". The "lateral surface area" is equal to 2 × 2 r × l (base l , height r , as opposed to 2 × 2 π r × l (where you take the perimeter of the circle and translate it).
See this problem
Log in to reply
Thank you for your explanation sir. I too did the same mistake as Aditya.
did exactly the same way... :-)
Wonderful problem Pranshu! I solved it by a pretty different method however... i'll just mention the method w/o getting into calculations.
- The lateral surface of the cylinder can be broken down into a series of 'strips' as follows...
- Establish a polar coordinate system on the top and bottom circles such that the reference axes are parallel to each other. Now consider a small section of the circumference at θ of length r d θ for both the circles. Thus we have a 'strip' joining these two small segments of length r d θ .
- The length of this strip is l (slant height) but width is not r d θ . This is where the confusion arises from.
- We need to find the angle ϕ between r d θ and l as a function of θ . Then the required lateral area equals ∫ 0 2 π l ⋅ s i n ( ϕ ( θ ) ) ⋅ r d θ ... where ϕ ( θ ) is the angle mentioned above.
- ϕ ( θ ) can be calculated by many methods but I preferred using vectors. Adopting a rectangular coordinate system the direction vector for r d θ becomes s i n θ i + c o s θ j and vector for l becomes 3 i + 4 k . Thus by dot products, etc. we get c o s ϕ = ( 3 / 5 ) s i n θ .
- Now its simply a job of putting everything together into that integral and evaluating it to get the answer and of course adding onto it the circular area part.
P.S. How to put those sketches into the text? Is there any software that you can use to make those sketches? (My solution would be better off with a diagram)
To calculate the surface area of an oblique cylinder, it is tempting to use a formula similar to the one used for a right circular cylinder, such as 2 π r ( r + l ) or 2 π r ( r + h ) . However for reasons I shall explain ahead, it would not be correct to do so.
The oblique cylinder consists of three surfaces: Two flat surfaces and one curved surface. Each flat surface is a circle with radius r , so the total area of flat surfaces is 2 × π r 2 .
Now we will find the area of the curved surface. Let us first define a few terms.
Lemma : The perpendicular cross sections of the oblique cylinder are elliptical and not circular.
Proof : Choose the coordinate axes such that the axis of the cylinder coincides with a coordinate axis, say the z-axis. The curved surface is now parallel to the z-axis, and the perpendicular cross sections are parallel to the xy plane.
In the following figure, we see the flat surface is highlighted in blue, and a perpendicular cross section is highlighted in green.
We know that the flat surface is a circle, and the perpendicular cross section is a projection of the circle, therefore the perpendicular cross section is an ellipse and not a circle. ■
Next we will cut a part of the cylinder along a perpendicular cross section and translate it as shown in the following figure. Observe that neither the lateral surface area, nor the volume of the cylinder is affected by this transformation. However, we obtain a right elliptical cylinder with the same perpendicular height as the slant height of our original oblique cylinder!
The area of the curved surface can now be found using "Perimeter of elliptical cross section × Height", i.e. P × l , where P is the perimeter of the elliptical cross section. P depends on the lengths of the semi-major and the semi-minor axis of the ellipse, so we will calculate those now. Let a and b be the semi-major and the semi-minor axes of the ellipse respectively.
Since we had projected the blue circle onto the green ellipse, i.e. we had projected along the y axis onto the xy plane, distances parallel to y axis are unchanged after the projection, and distances along the x axis are reduced. Thus the semi-major axis of the elliptical section is parallel to the y axis and is equal to the radius of the flat surface, r , and the semi-minor axis is parallel to the x axis. Now we will find the semi-minor axis of the ellipse.
We will now use the invariance of volume to calculate the length of the semi-minor axis of the ellipse. Recall that the area of an ellipse with semi-major axis and semi-minor axis a and b is π a b .
Also recall that the volume of the original oblique cylinder could be written as "Area of base × Perpendicular height" = π r 2 × h .
Similarly, the volume of the newly formed right elliptical cylinder is π a b × l . Since the volume of both the cylinders is the same, we can equate them.
π r 2 × h = π a b × l
We have already derived that a = r , so let's substitute it in the above equation and make b the subject of the formula.
π r 2 × h = π r b × l ⟹ b = r × l h ( 1 )
We see that the semi-major axis of the ellipse is r , and the semi-minor axis is r × l h .
Now that we know a and b in terms of the given data, we can proceed to find the value of P . Unfortunately a closed form of the perimeter of ellipse does not exist. We can make use of an infinite series, such as the Gauss-Kummer Series to get the approximate value of the perimeter. The first few terms of the series are
P = π ( a + b ) ( 1 + 4 1 k 2 + 6 4 1 k 4 + 2 5 6 1 k 6 + ⋯ ) ( 2 )
where k = a + b a − b .
After substituting values of r , h and l in equation ( 1 ) , we get a = 2 and b = 5 8 . Using this, we see that k = 9 1 .
Substituting values of a , b and k in equation ( 2 ) , we obtain P ≈ 1 1 . 3 4 4 6 7 .
The total surface area of the oblique cylinder is the sum of the areas of the flat surfaces and the curved surface.
S = 2 × π r 2 + P × l ( 3 )
After substituting r , l and P in equation ( 3 ) , we get S ≈ 8 1 . 8 5 6 □
To conclude, the only correct way to find the lateral surface area of any cylinder whose flat surfaces are parallel and congruent to each other (irrespective of whether the cylinder is right or oblique) is
Lateral Surface Area = Perimeter of Perpendicular Cross Section × Length of Axis
Using the perimeter of any other cross section will yield incorrect results. In case of the right cylinder, the flat surface is the same as the perpendicular cross section so it is not much of an issue there. However, special care must be taken in the case of an oblique cylinder, where the flat surfaces and the perpendicular cross sections are not the same.
The formulae stated at the beginning of the solution use a circular cross section. The circular cross section is not perpendicular to the axis of the cylinder, so it gives an incorrect answer. This concept is nicely summarized on this webpage: http://www.mathalino.com/reviewer/solid-mensuration/cylinder