Now that's what I call a series! Number 2

Algebra Level 4

∑ m = 1 ∞ m 3 + ( m 2 + 1 ) 2 ( m 2 + m ) ( m 4 + m 2 + 1 ) \large \sum_{m=1}^\infty \frac{ m^3 + (m^2+1)^2}{ (m^2+m)(m^4+m^2+1) }

If the series above can be expressed as A B \frac AB for coprime positive integers A A and B B , find the value of A + B A+ B .


The answer is 5.

View wiki
Aditya Tiwari by Aditya Tiwari , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Pi Han Goh
Jun 18, 2015

We begin by rearranging the numerator of the given fraction, m 3 + ( m 2 + 1 ) 2 = ( m 4 + m 2 + 1 ) + ( m 3 + m 2 ) m^3 + (m^2+1)^2 = (m^4 + m^2 + 1) + (m^3 + m^2) .

So m 3 + ( m 2 + 1 ) 2 ( m 2 + m ) ( m 4 + m 2 + 1 ) = 1 m ( m + 1 ) + m 2 ( m + 1 ) m ( m + 1 ) ( m 4 + m 2 + 1 ) = 1 m − 1 m + 1 + m m 4 + m 2 + 1 \frac{ m^3 + (m^2+1)^2}{ (m^2+m)(m^4+m^2+1) }= \frac1{m(m+1)} + \frac{m^2(m+1)}{m(m+1)(m^4+m^2+1)} = \frac1m - \frac1{m+1} + \frac{m}{m^4+m^2+1} .

Note that we can factorize m 4 + m 2 + 1 m^4 + m^2+1 to ( m 2 − m + 1 ) ( m 2 + m + 1 ) (m^2-m+1)(m^2+m+1) .

By partial fraction, we get m m 4 + m 2 + 1 = 1 2 ( 1 m 2 − m + 1 − 1 m 2 + m + 1 ) \frac{m}{m^4+m^2+1} = \frac12 \left( \frac1{m^2-m+1} - \frac1{m^2+m+1} \right) .

Denoting a m = 1 m 2 + m + 1 a_m = \frac1{m^2+m+1} , then a m − 1 = 1 m 2 − m + 1 a_{m-1} = \frac1{m^2-m+1} . By telescoping sum,

∑ m = 1 ∞ m 3 + ( m 2 + 1 ) 2 ( m 2 + m ) ( m 4 + m 2 + 1 ) = ∑ m = 1 ∞ [ ( 1 m − 1 m + 1 ) + 1 2 ( a m − 1 + a m ) ] = 1 1 + 1 2 a 0 = 3 2 \begin{aligned} &&\displaystyle \sum_{m=1}^\infty \frac{ m^3 + (m^2+1)^2}{ (m^2+m)(m^4+m^2+1) } \\ &=& \displaystyle \sum_{m=1}^\infty \left[\left( \frac1m - \frac1{m+1} \right)+ \frac12 \left(a_{m-1} + a_m\right) \right] \\ &=& \frac11 + \frac12 a_0 = \frac32 \\ \end{aligned}

12 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Great telescoping sum approach.

How can one motivate this?

Challenge Master: Well, basically it's a sum of many terms, it's common to consider Telescoping Sum as a viable approach. If this is not possible, then I may need devise other techniques to solve this. For example, ∑ n = 1 ∞ 1 n 2 + 1 \displaystyle \sum_{n=1}^\infty \frac1{n^2+1} is not solvable by Telescoping Sum, so I may consider Riemann Sum or some other more advanced approach.

TL;DR: Always try telescoping sum first.

Pi Han Goh - 5 years, 11 months ago

Well done!

Chew-Seong Cheong - 5 years, 12 months ago

Log in to reply

THANK YOU!

Pi Han Goh - 5 years, 12 months ago

Log in to reply

nice solution

Prakhar Bindal - 5 years, 5 months ago

Log in to reply

@Prakhar Bindal – THANKYOU!!!!

Pi Han Goh - 5 years, 5 months ago
Shashank Rustagi
Jun 17, 2015

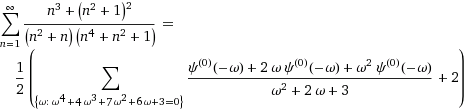HENCE 1.5 that is 3/2 i.e 3 + 2 =5

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Please provide a complete solution explaining the steps that you did.

Do not simply use a computing device without understanding the work that is involved.

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...