NSEJS 2015 Problem 2

I just used process of elimination:

There will be a triangle formed with side lengths of 20, 30, and x; where x is the length of the missing diagonal. The Triangle Inequality says that the sum of the two shorter sides is greater than the length of the longest side.

100 $\sqrt{5}$ is not the answer, because 100 $\sqrt{5}$ > 20 + 30

5 $\sqrt{2}$ is not the answer, because 30 > 20 + 5 $\sqrt{2}$

10 $\sqrt{10}$ is a possible solution, because 10 $\sqrt{10}$ < 30 + 20

50 is not the answer because 20 + 30 = 50.

Since a, b, and d are impossible; the answer must be $\boxed{10\sqrt{10}}$

I use the law of cosines:

400^2 = 30^2 +20^20 - 2 (30)(20)cosC C = 104.5°

This is the measurement for the angles not cut by the 40m diagonal.

Then : 180° - 104.5° = 75.5° is the measure of the other pair of angles.

Then I use the law of cosine again to find the length of the other diagonal.

C^2 = 30^2 + 20^2 - 2 (30)(20)cos (75.5) C = sqrt (1000) = 10 sqrt (10)

• I apologize for the format but I am working from my cell phone.

Can't we use the parallelogram law? Sum of the squares of the sides of the parallelogram = Sum of the squares of the diagonals.

I used it and got the right answer;

20^{2} + 20^{2} + 30^{2} + 30^{2} = 40^{2} + x^{2}

2600= 1600 + x^{2}

x^{2}= 1000

x= 10 sqrt{10}

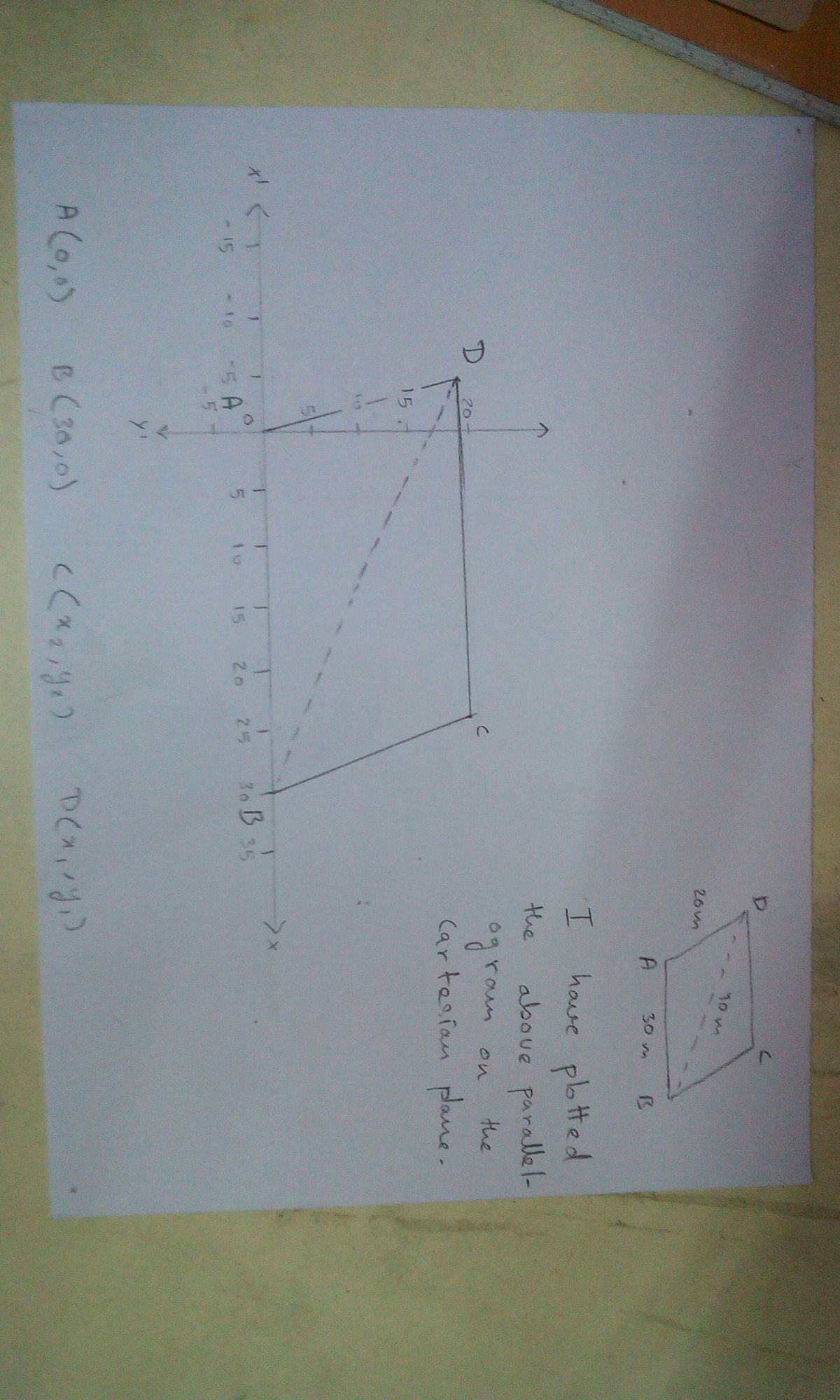
I used co-ordinate geometery to solve the problem,

After I had plotted the quadilateral(As shown in the image), I had to determine the value of co-ordinates of point D,

$20^{2}=(x_{1}-0)^{2}+(y_{1}-0)^{2}$

$400=(x_{1})^{2}+(y_{1})^{2}$

Now,

$40^{2}=(x_{1}-30)^{2}+(y_{1}-0)^{2}$

$1600=(x_{1})^{2}+900-60(x_{1})+(y_{1})^{2}$

Placing values,

$700=400-60(x_{1})$

$x_{1}=-5$

And, $y_{1}=\sqrt{375}$

Now co-ordinates of point C,

$x_{2}=30-0+(-5), y_{2}=0-0+\sqrt{375}$

$x_{2}=25, y_{2}=\sqrt{375}$

Now we just need to find the distance AC,

$(AC)^{2}=(25-0)^{2}+(\sqrt{375}-0)^{2}$

$AC=\sqrt{(625+375)}$

$AC=\sqrt{1000}$

$AC=10\sqrt{10}$

I used Appolonius Theorem.