Obtaining the perfect volume of petrol
You need 8 liters of petrol. Using two containers that can hold 12 and 9 liters, you can do any of the following actions as many times as you like:
- fill a container to its brim;
- completely empty a container;
- pour petrol from one container to another.
Is it possible to get exactly 8 liters (in either container)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Well done
I have an alternative geometrical method, see my solution for Petrol problem
Log in to reply
I'd like to see your generalized method in Petrol problem here among the solutions. It's really nice!
Could you please explain the intution behind this? Why the 60 degree slant? What us the formal name of the method so I can self-study it?
Log in to reply
@Navkiran Singh – Thank you for your question. The branch of mathematics that is used for these types of problems is called Barycentric Coordinates. When coupled with terms like “fill jugs,” an Internet search will produce a number of hits that go through the boundary conditions and explain why equilateral triangles are used (thus the 60 degree slant). Wolfram has a web page under “Water-Pouring Problem” with an applet that walks you through several examples (but without a lot of explanation).
@Navkiran Singh – I found a nice video on the "Mathologer" website, under the title "How not to Die Hard with Math." The reference is to a scene in the Bruce Willis movie, where he and another guy have to solve a jug-filling problem quickly, to prevent a bomb from going off. Just after the 3:00 mark, the Mathologer begins building the parallelogram for the Die Hard problem and explains in detail how/why it works. I don't know if we are allowed to include Internet links, so I didn't, but the description will make it simple to find. Hope this helps with your self-study of barycentric coordinate systems!
Very nice answer. Thank you very much
Question didn't make any sense because, of course 8 will fit into 9 or 12.
Log in to reply
The idea is that without markings, there is no way to know EXACTLY how much 8L is. You can only know that the container has 12 or 9 liters of gas when either one is full, or if you do something like empty the 12L and pour all the gas from the 9L into the 12L container, at which point the 12L would contain 9L of gas. Of course both containers can contain over 8L, but the question is asking if it is possible to get exactly 8L using only the three actions mentioned
Beautiful solution, elegant and so complete! So cool when problems like these can be solved geometrically! Hats off :D
A really nice approach! Thumbs Up!
I'm not the only one thinking of filling the 9 and 12 liter jugs and then pouring 4L into the already full 9L (thus spilling the petrol) so that the 12L will have 8L in it, am I?
Log in to reply
@Nakito Koyuarto - In these problems, the containers are not graduated; they carry no intermediate markings. All we know is that one container, when full, holds 12L, and the other container, when full, holds 9L. We have no way of knowing how to pour exactly 4L out of the full 12L container.
Strictly speaking the puzzle implies that you start at the bottom left with (0,0). You can then head off in one of two directions, either towards (12,0) or towards (0,9). Either way, if you keep going long enough you will arrive back at (0,0) without achieving your objective of 8 litres.
Log in to reply
@Paul Cockburn - Very good point! Starting at (0,0) mimics the initial conditions for the problem. Thanks.
This offers solutions that are not possible without a third container. For instance, how would you achieve 0,6 or 6,0?
Log in to reply
@Ken Stern – The beauty of the diagram is that it contains instructions that answer your question. To get to (6,0) and (0,6), one way is to begin at (0,0), move horizontally to (12,0) and enter the red path. The step-by-step instructions:
• (0,0) both cans empty
• (12,0) fill the 12L can
• (3,9) fill the 9L can from the 12L can, leaving 3L in the 12L can
• (3,0) empty the 9L can
• (0,3) transfer 3L from the 12L can to the 9L can, leaving the 12L empty
• (12,3) fill the 12L can
• (6,9) fill the 9L can from the 12L can, leaving 6L in the 12L can
There are now 6L in the 12L can; all that remains to do is to empty the 9L can for (6,0) and then pour the 6L into the empty 9L can for (0,6).
this is the most valid solution i ever meet! cool!
Log in to reply
@Zwt Zwt - Thank you. The branch of mathematics that is used for these types of problems is called Barycentric Coordinates; the diagrams generally consist of equilateral triangles (hence the 60 degree slant in the figure I posted). It also works for solving three-container problems, which is where I was first introduced to barycentric coordinate systems.
I found a nice video on the "Mathologer" website, under the title "How not to Die Hard with Math." Just after the 3:00 mark, the Mathologer begins building the parallelogram for the Die Hard problem and explains in detail how/why it works ("Die Hard" is well-known American movie with a fluid-pouring problem as part of the plot).
can we use this method for any bareel (suc as 4lt and 3 lt)
Log in to reply
@Muhammed Ali Yeşilkır - Absolutely! The branch of mathematics that is used for these types of problems is called Barycentric Coordinates; the diagrams generally consist of equilateral triangles (hence the 60 degree slant in the figure I posted). To size the parallelogram, just use whatever volumes you are given for the containers; the “red path” will walk you through the fluid-pouring steps and get you to any results that are possible for that set of containers.
It also works for solving three-container problems, which is where I was first introduced to barycentric coordinate systems.
You sometimes see a variant with 3-gallon and 5-gallon containers, titled the “Die Hard” problem; the reference is to a scene in the Bruce Willis movie, where he and another guy have to solve a jug-filling problem quickly, to prevent a bomb from going off. Of course, they solve it without drawing diagrams, but the popularity of the movie prompted renewed interest in application of barycentric coordinates to fluid-pouring questions.
I found a nice video on the "Mathologer" website, under the title "How not to Die Hard with Math." Just after the 3:00 mark, the Mathologer begins building the parallelogram for the Die Hard problem and explains in detail how/why it works. Hope this helps!
Whem they say "pour petrol from one container to another." The quality of petrol wasn't specified.
Since 12 and 9 are both multiples of 3, the only volumes that can be obtained exactly will also be multiples of 3.
You can use Linear Diophantine equations to solve this problem. The problem takes the form 12x + 9y = 8 for some integer values of x and y. By Bezout's Lemma, we know that this equation only has solutions if the answer is divisible by the gcd of 12 and 9. The gcd of 12 and 9 is 3, which 8 is not divisible by. Hence we have our answer.
Log in to reply
Please post this as a solution
Log in to reply
I'm new to this site; not sure where to go to post one
Log in to reply
@Joel Anyanti – If you are using your computer, scroll up above Zico's answer and below the problem; there should be a space (not a button). On the app, I think you are only able to reply.
How did you know to which numerical values you assigned your x and y in this equation?
This is how I got my right answer.
Technically, the question is setup into two bullets, and there is no instruction saying that you cannot use both bullet points to find your answer. Secondly, the first bullet point has a semicolon at the end, which would mean that it combines bullet one and two with the conjunction "and." Therefore, since we are allowed to use both actions to find the solution, you can pour all 9 liters of the can out, and then precede to pour 8 liters in, which is allowed by the first bullet point. I understand that the math cannot be done with just one bullet point, but if that is the case there must be instructions that specifically inform you to choose between one bullet point or the other, which it did not. Fix this stupid question please.
Log in to reply
Hello Eric. A semicolon does not necessarily indicate a conjunction "and". It merely indicates a continuation of the sentence/thought. I have clarified the problem so that this is more clear.
Log in to reply
That is true. It is great to see that staff took the time to give me feedback. Thank you.
But if we have another odd bucket...We can make 8L. No ?
Log in to reply
Unless it's an odd multiple of 3... A 15L extra bucket wouldn't really help, would it? ;-)
I think that it is completely possible since the third thing you can do is not "pour ALL the patrol from one container to another" so you can just fill up one container and pour 8 litres into the other.
Log in to reply
(Assuming you are not deliberately missing the point...) Yes, you could do that, but how would you know when you had poured exactly 8 litres? The actions listed enable you to know exactly how much is in each container at each stage of the process. Other actions would have to be mere estimates.
Log in to reply
That is a good point, but the instructions do not really make that clear.
Empty the 12 gallon.Go to the carryout and buy 8 gallons of water. Fill 12 gallon
Log in to reply
Or if you are talking gas then go to the pump with an empty 12 gallon
easy to understand. thanks.
A volume is obtainable if and only if it is a multiple of the gcd of 12 and 9 - that is a multiple of 3. But 8 is NOT divisible by 3.
Exactly what I was thinking
Why it is related to gcd
Log in to reply
Because of Bézout's identity, the GCD can be obtained by adding and subtracting the original numbers a few times. :-B
Relevant wiki: Greatest Common Divisor - Problem Solving

Using the general method, we get the equation 1 2 a + 4 = 9 b , where a and b are integers
Listing out possible values of 1 2 a + 4 and 9 b , there will be no integer values of a and b to satisfy this equation so 8 can never be obtained.
General method of solving
I'll be using this question as an example to explain.
++ means filling it to the brim
-- means emptying
--> means transfer to the right can
<-- means vice versa
You would realise that there are only ++ on the left, -- on the right and only -->,
because doing the opposite will always result in working backwards, which is counter-productive (you won't get new integers)
Whenever we transfer to the right we will get either (x, 19) or (0,y), where
0 < x < 13
0 < y < 19
(x, 19): If we empty the left, we will get (0, 19), deleting our ‘new value’ (not productive)
(0, y): If we fill the right, we will be ‘masking our new integer’ which does not help at all
Since we started with 13 and then transferred right, we cannot do otherwise but add on the left, empty the right and transfer right. This only allows us to do the same and so on.
General formula
Now, let's look at this geometrically/graphically:
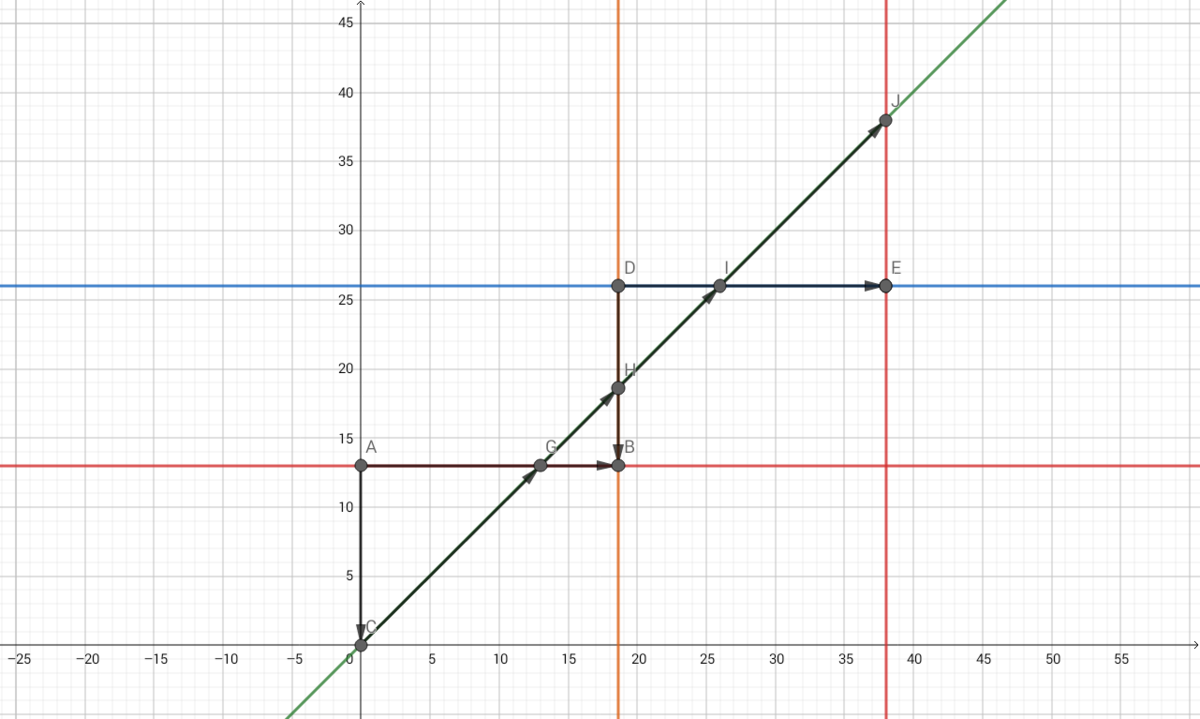
This geometric representation follows the rule that we can only refill the left, transfer right and empty the right. I recommend you to study the graph and do some arithmetics to prove that it is an appropriate representation
After that, you will realise that this has something to do with modulus as the containers gets filled and emptied, just like the remainnder of x / 3
The arrows pointing down represent the 13-litre can
The ones pointing right represent the 19-litre can
A line of gradient 1 is drawn from the origin
At (0,0), the y-value matched the tip of vector AC, meaning that the 13 is full
The x-value matched the base of vector AB, meaning that the 19 is empty
When the graph y = x touches vector AB, it means that 13-litres have been transferred (isosceles right angled triangle)
The y-value corresponds to the base of vector AC and the tip of vector DB, meaning that the left can is empty and it is going to be refilled
When the graph intersects vector DB, it means that an “emptiness” of 6 litres have been transferred from 19-litre can to the 13-litre can because vector AB and DB meet with their arrows pointing towards each other rather than away
This representation follows the rule that we can only add on the left, empty the right and transfer right in order to take the minimum number of steps
From the graph, we know that the 13-litre can is going to contain our desired integer first.
Every intersection point on the graph represents two things:
- The refilling of 13-litre can
- The emptying of the 19-litre can
Each vector of gradient 1 also represents the transferring step
Since the points land on the horizontal and vertical vectors, the number of points are equal to the number of horizontal and verical vectors
Hence, if we want to get 1 litre, the number of steps is equal to 4 intersecting points + 4 vectors of gradient 1 = 2 x 4 intersecting points = 2 x (2 horizontal + 2 vertical) = 8
Notice that I ignored the last point J since it implies emptying the 19-litre so I did not draw and count the last '13' vector
We can formulate this equation from the graph
1 9 a = 1 3 b + 1 2 rather than 1 9 a = 1 3 b − 1 since we ignored the 3rd '13' vector
Note that the b in the second equation is one more that the other b in the first equation.
Where a and b are integers
a represents the number of ‘19’ vectors
b represents the number of ‘13’ vectors
This is also asking of what is the number that is divisible by 19 and leaves a remainder of 12 when divided by 13
The number is 38 and
a = 2 , b = 2
This is equal to 4 × 2 = ( a + b ) × 2 = 8 , which is proved correct
General method of solving:
Let x and y be the maximum integer volumes
Let a and b be integers
Let r be the remaining volume you want to obtain
a x + ( x − r ) = b y for starting with x
Solve for a and b using the Chinese Remainder Theorem
Add a and b then multiply then by 2 and there you go!!
Using the method to get a remainder of 8 litres:
1 3 a + 5 = 1 9 b
a = 4
b = 3
Ans: 14
We will get 46 if we started with 19
By the way, the graph can be compacted, being very similar to A lot of reflections and Law of reflection
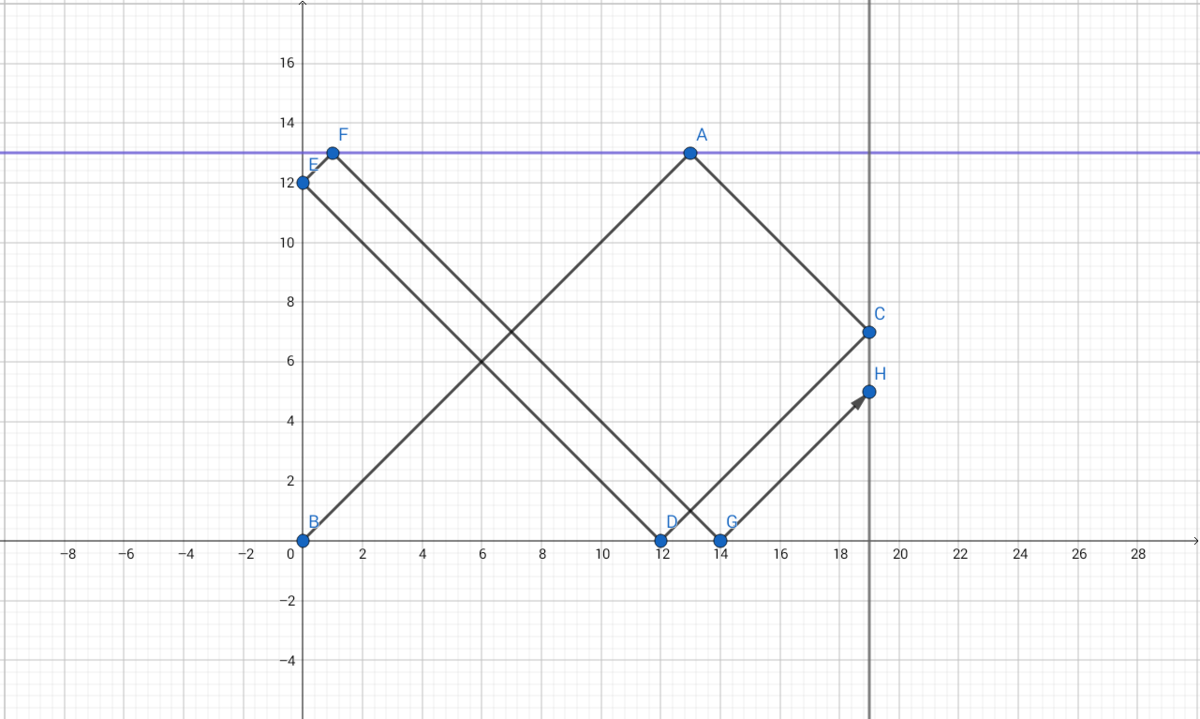
Oh wow, a very detailed yet simple to understand geometrical/graphical approach. Probably the most convincing solution among all the solutions here. Thanks for sharing!
There must be a third container that is 2L to get 8
There must be a 2L container? What about a 1L container? or a 4L container?
12 and 9 litre cans can only accommodate multiples of 3 between them. It is impossible to obtain 2L from any sequence.
Guys, Exactly 8L each would ammount to 16L in total. And initially there are 17 (12+9) L, hence it would never be possible to 17=16.
This graphical solution not only shows what volumes are possible, but lists, in order, the actual filling/emptying steps needed to get to any desired volume (if it is possible to do so).
This graph has dimensions 12 x 9, and is set at a 60 degree slant. Start at the bottom right (12,0), travel at a 60 degree angle up to the top (3,9) and continue with 60 degree reflections as long as you are able. The coordinates tell you what to do:
(12,0) start with the 12L can full and the 9L can empty.
(3,9) fill the 9L can from the 12L can (leaving 3L in the 12L can)
(3,0) empty the 9L can.
(0,3) transfer the 3L contents of the 12L can into the 9L can.
The red path terminates at (0,9) without ever touching on a boundary coordinate with the value 8 in it, so it is not possible to get exactly 8L in either can.
You can also start from the top left of the graph (0,9) - with the 12L can empty and the 9L can full - and go backwards over the same red path.
It takes quite a while to set up the graph, but - once you have it - the red path will tell you, step-by-step, the fill/empty operations necessary to produce any desired volume that is possible.