Octo-parallelogram!
Given any parallelogram, draw two line segments from each corner to connect to the midpoints of the opposite sides. These eight line segments form an octagon, as shown above.
Let O be the octagon's area and let P be the parallelogram's area. To three decimal places, what is P O ?
The answer is 0.1666666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
It's good to see that these solutions deal with the parallelogram, instead of just the degenerate case of a square (which is often used as a contest trick). This makes the solution fully general from the start. For this problem, as it turns out, we can prove it for the square, and extend the argument to the parallelogram:
-
Prove that for a square (with side length as the shorter side of the parallelogram), the octagon area is 1/6 of the square.
-
Shear the square horizontally, till the vertical side length equals the longer side of the parallelogram. Since areas are preserved, we can conlude that the octagon area is 1/6 of the parallelogram.
Here is another problem where a similar idea of generalizing from a special case works .
Excellent solution, Utkarsh! The solution just boils down to partitioning the parallelogram (as well as the octagon) into smaller "manageable" chunks of symmetrically-known area. Here's a YouTube link that inspired me to post this prob!
https://www.youtube.com/watch?v=rwDgfxTulpI&t=1s
Log in to reply
Thanks. I also absolutely enjoyed solving the problem. But I don't seem to be able access your video, can you please try providing the direct link?
Log in to reply
Actually, you can just copy/paste the link in your browser.....should take you right there!
Log in to reply
@Tom Engelsman – Actually I was on mobile, and I tried rewriting the URL on browser but it won't work.
Log in to reply
How did you calculate the last step please? (How did you add/subtract the parts?) Also, how does one solve a problem like this so elegant?
Log in to reply
Just combining like terms. A - (8A / 4 - 4A / 6 - 4A / 8) = 1A - 2A + (2/3)A + (1/2)A = (1/6)A
Log in to reply
Sorry, i meant the step leading to that. I know A/4 is the area of the triangle formed by joining the midpoint of one side with any opposite corner, I know A/6 = MOND and A/8 = SYR. But how to add them together to subtract from the large parallelogram?
Im pretty confused and cant seem to figure out what im doing wrong, but i cannot get the 1/6 or 0.166 ratio. I have devolved the problem from a parallelogram to a square, just to make things simple. So for a square of side 8, we would get an octagon of radius 2. Area of such an octagon is 2 * root 2 * 4 , i.e. 8 * root 2. And the area of the square is 64. Hence the ratio comes out to be 0.176 and not 0.166. This is frustrating me, im sure its some small detail that i have completely overlooked, but for the life of me, i cannot find that damn small detail lol
Log in to reply
It isn't a regular octagon (check the angles).
Log in to reply
Youre right! I drew a free hand diagram and thought it looked regular, terrible assumption on my part. Thanks Jason.
Let the parallelogram's area be P and the octagon's area be O . Then, connect the midpoints of the parallelogram, dividing the parallelogram into quadrants. These should also pass through vertices of the octagon. Divide one of the quadrants in a similar fashion. The result will look like this:
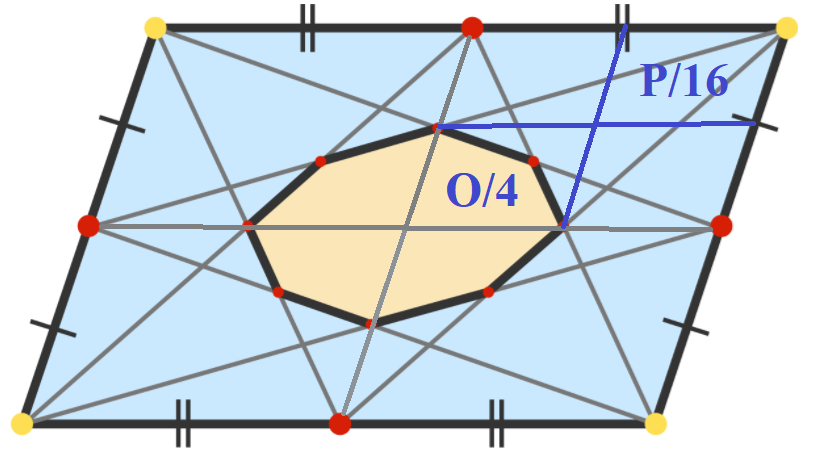
Each small quadrant's area is 1 6 P , and the octagon is divided into shapes with area 4 O . Now, we will zoom in on the octagon quadrant and divide it into four (we will focus on these smallest quadrants from this point onward).
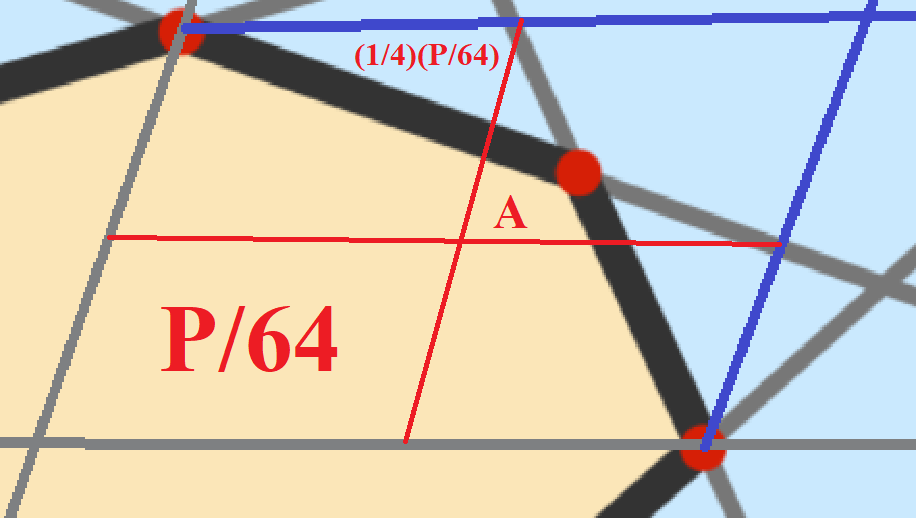
Part of the octagon is in each of these quadrants of area 6 4 P . Look at the top left quadrant. A triangle is formed in the space between the octagon and the quadrant boundaries. We can see that the triangle has an area equal to one-fourth of the quadrant. The area of the orange shape in this quadrant, then, is 4 3 × 6 4 P = 2 5 6 3 P . A similar argument can be made for the bottom right quadrant.
Our final quadrant contains an orange shape labeled A that has all the same angles as the entire section of the octagon in this image, so the shapes are similar. Since the area of the large orange shape is 4 O , and A has sides scaled down by 4 1 , A = 4 1 × 4 1 × 4 O = 6 4 O . Now we have an equation:
4 O = 6 4 P + 2 5 6 3 P + 2 5 6 3 P + 6 4 O
6 4 O = 4 P + 3 P + 3 P + 4 O
6 0 O = 1 0 P
P O = 6 1 = 0 . 1 6 6 6
I didn't come up with this solution. Credit goes to Presh Talwalkar's video .
By applying a shear, one may assume the parallelogram is a rectangle (whose sides are parallel to the x and y axis). Furthermore, since we are only interested in the ratio of these area, stretching (that is dilating along the x-coordinate but not the y-coordinate) does not change the answer. So one may assume we are dealing with a square (whose center is at the origin). Each quadrant has a 1/4 of the area of the octagon and 1/4 of the area of the square. So we may only consider the ration in the first quadrant. The part of the octagon in the first quadrant is a kite whose corners have coordinate (0,0), (0,1/2), (1/2,0) and (1/3,1/3). [The last coordinate can be computed by intercepting the two lines y = (1-x)/2 and y =1-2x, the other are obvious].
There are many ways to compute the area of this kite. One can split it into two equal triangles (split using the line from (0,0) to (1/3,1/3) ). Each triangle has height 1/3 and basis is 1/2 (this can be read directly from the coordinates). The area of the kite is 1/6. The square has area 1, so the the ratio is 1/6.
Nice! Any transformation that does not change the ratio of the areas and makes the calculation simpler is valid and good math practice. Working with the square (or quarter of square) does not make the solution less general, as you said.
你可以把一个平行四边形本质看作正方形,平行四边形只是换了一组基底表示某一向量空间中的正方形。以正方形左下角顶点作为原点建立直角坐标系求解出八边形的八分之一(一个三角形)的面积,以求得结果。
much easier to work with a square ( just a particular type of parallelogram), the solution becomes not too complex
But a square is more specific than a parallelogram, the fact that it works for a a square does not it does not imply that it works for a parallelogram. (It does in this case, but I just pointing out the logical fallacy.)
Log in to reply
I know. It is obvious. However, I do not need to demonstrate anything. I just have to solve a problem. The statement talks about "ANY parallelogram". I am allowed to work with the parallelogram that is more comfortable.
Log in to reply
In THIS CASE, the problem with a square (the most "specific" parallelogram of all) "generalizes" to the same problem with any parallelogram. However, IN GENERAL, showing something that something works (is true about) a square DOES NOT imply that it holds for any parallelogram, because a square has special properties that not all parallelograms have, and these special properties will cause some things to "work" for a square and not for all parallelograms.
Affine transformations preserve the ratio of the areas.
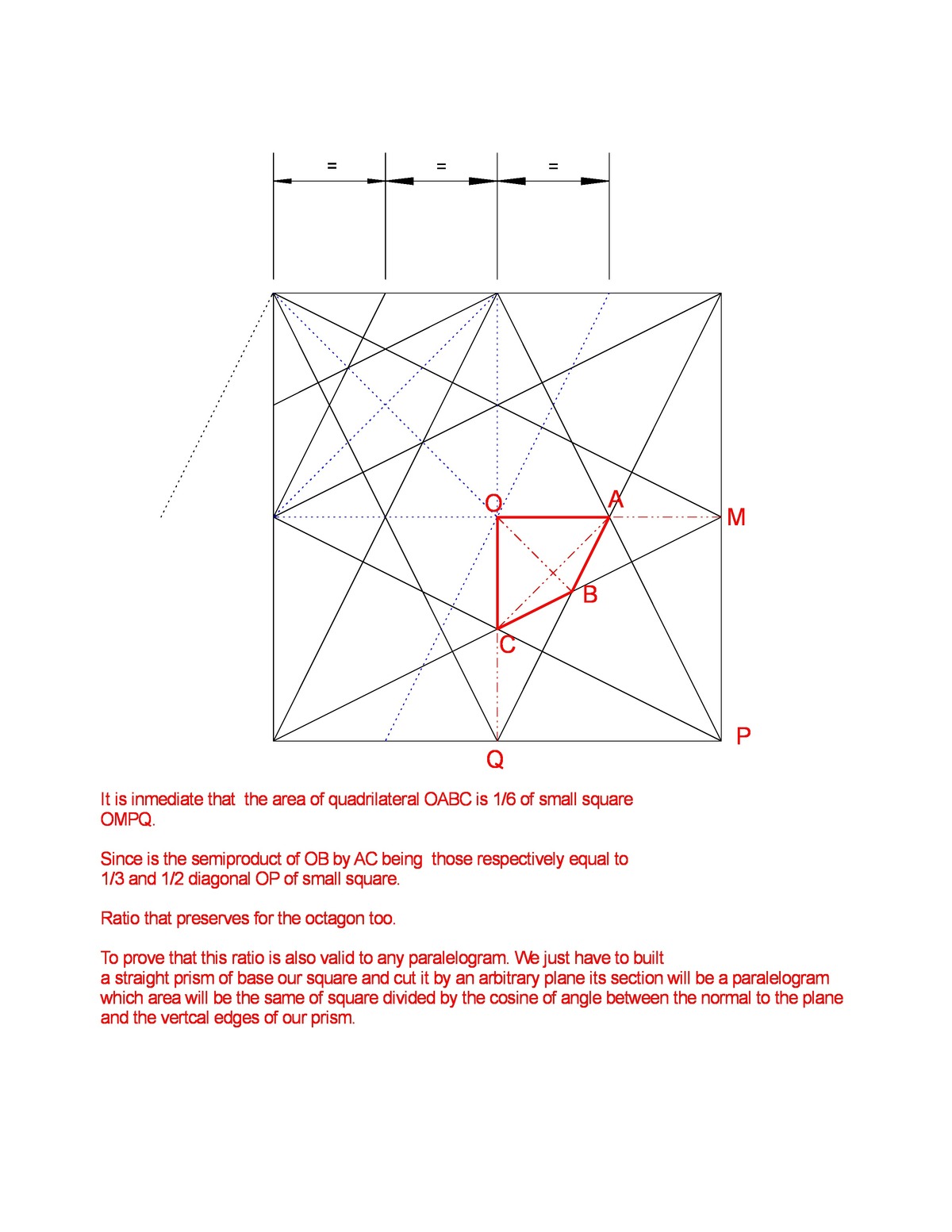
Let area of the parallelogram be A then it follows the area of the triangle formed by joining the midpoint of one side with any opposite corner will be 4 A . This is the image
This is the image
Consider the two diagrams, we will attempting to find out the area bounded by regions similar to M O N D and that by regions similar to S P R .
Let x be the area of D N O and y be area of D O M , based on the property of median dividing the triangle into two triangles of equal area other areas are labeled.
Now, M O N D = 3 ( 2 x + y ) + ( 2 y + x ) = 6 A
For the other diagram, it can be proved that X S R Z is indeed a parallelogram with area half as A / 2 , which means area of S Y R is A / 8 .
By inclusion and exclusion of area and some thought it can be said that the area of octagon is A − ( 8 × 4 A − 4 × 6 A − 4 × 8 A ) = 6 A