Odd and Even Pyramids
In the graph below, the number in any box is the sum of the two numbers below it. The bottom numbers can be anything. What is the maximum possible amount of odd numbers that can be used in the pyramid?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem and solution! Can it be generalised? How many odd numbers can we get in a pyramid with n cells in the bottom row?
Log in to reply
I don't know, thanks for the idea. I'll try and see if I can find something out.
@Chris Lewis , A couldn't make a formula, but I created a Python Code. Here it is:
#You can out whatever number you want for N, the number of cells in the bottom row.
N = 3
T = 4
CN = 0
while N != 0:
if N+2 >= T:
if N >= T:
CN = CN + T*(T+1)/2
CN = CN - (T-1)
CN = CN - {(T-3)*(T-2)/2}
T = T+3
elif N+1 = T:
CN = CN + (T-1)*T/2
CN = CN - {(T-1)*2/3}
CN = CN - {(T-3)*(T-2)/2}
T = T+3
elif N+2 = T:
CN = CN + (T-2)*(T-1)/2
CN = CN - {(T-1)*1/3}
CN = CN - {(T-3)*(T-2)/2}
T = T+3
elif T > N+2:
print (CN+1)
Using the above pattern, it can be verified inductively that the maximum number of odd numbers for n cells in the bottom row is ⌊ 3 1 ( n 2 + n + 1 ) ⌋ .
Log in to reply
Oh okay, I don't know stuff that is that complex yet.
Log in to reply
@Nicholas Benedict – I'm sure you will eventually, especially if you're thinking about great problems like this one!
Thank you for the formula though, @David Vreken
Log in to reply
@Nicholas Benedict – I searched it up online an figured out that it was a rounding symbol
@David Vreken How did you figure out the formula
Log in to reply
@Aditya Mittal – I found the first few sums of odd numbers for the first few rows:
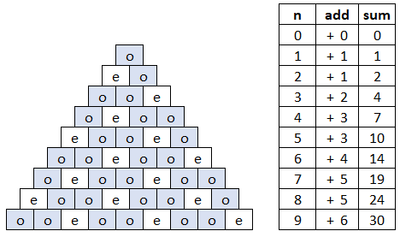
and I noticed the sums follow a pattern for every third row.
For rows n = 1 , 4 , 7 , . . . , the sums are 1 , 7 , 1 9 , . . . which follows the equation 3 1 ( n 2 + n + 1 ) .
For rows n = 2 , 5 , 8 , . . . , the sums are 2 , 1 0 , 2 4 , . . . which follows the equation 3 1 ( n 2 + n ) .
For rows n = 3 , 6 , 9 , . . . , the sums are 4 , 1 4 , 3 0 , . . . which follows the equation 3 1 ( n 2 + n ) .
So in summary we have a sum of ⌊ 3 1 ( n 2 + n + 1 ) ⌋ for all values of n .
Log in to reply
@David Vreken – Your answer is just awesome. :)) But I wanna point out one thing-----
The number of rows in the pyramid = no. of cells in the bottom row = n (always true)
Now n can be in any of these three forms: 3m, (3m+1), (3m+2), where m is an integer.
When n= 3m or 3m+2, Max odd no.s in the pyramid= [⅓(n^2 + n)]
When n= 3m+1, Max odd no.s in the pyramid= [⅓(n^2 + n+ 1)]
You actually wrote the correct answer just the last statement was a bit wrong. :)
Log in to reply
@Guddu Banerjee – Are you saying that this statement is incorrect: "So in summary we have a sum of ⌊ 3 1 ( n 2 + n + 1 ) ⌋ for all values of n "? (Don't forget I added the floor function around it to adjust for the differences between 3 1 ( n 2 + n + 1 ) and 3 1 ( n 2 + n ) )
Rounded[2n/3] ? Up or down, both. Oh, this is only for the bottom row, took the question wrong.
The real thing that is surprising about this problem. This is my third problem and many people tried it in just 1 DAY!
Log in to reply
Thank you everyone for doing this problem!
Log in to reply
Not a problem! I have posted the follow-up problem , following that your problem became popular.
Here is another layout.
My thinking is bottom-up, always keeping symmetry about the midline.

I used the exact same line of thought :)
There are many solutions to this problem, but we only need to know one:
Lets start from the top and work our way down.
First, the top number can be odd or even, lets make it odd.
There is only one way for the second row, an odd and an even.
For the third row, on the even side, we can use two odds, and then use an even, because even plus odd equals odd.
For the fourth row, we can use three odds and an even like this:
And for the fifth and final row, we can use this configuration to get the max number of odds:
If we count up the total amount of odds, we get 1 0 odds.