Odd-Even elimination

Binary number approach

Subtract 1 from all numbers and positions, and write them in binary notation. (Thus, 000 is at position 0, 001 at position 1, and so on.)

After the first step, only the numbers ending in 1 survive, and their new position number is obtained by removing the 1. (Thus, 001 at position 0, 011 at position 1, etc.)

After the second step, only the positions ending in 0 survive, which are all numbers ending in 01, and their new position is obtained by removing 01. (Thus, 001 at position 0, 101 at position 1, 1001 at position 2, etc.) After the $n$ th step, the surviving number in position $a$ is $\overline{a \underbrace{\dots 010101}_{n\ \text{digits}}}$ .

Since $2^{13} < 12345 < 2^{14}$ , we can perform 14 steps before we end up with $01010101010101_2 = 5461_{10}$ at position 0. Adding back in the 1 we subtracted, the answer is therefore $\boxed{5462}$ .

By way of generalization, any binary number following the patter $x = 10101\dots101_2$ satisfies the equation $4x + 1 - x = 4^n\ \ \ \ \ \therefore\ \ \ \ \ \ x = \frac{4^n-1}3$ for some integer $n$ . Thus, with $n = 6$ we obtain $x = (4^6 - 1)/3 = 1365$ , and with $n = 7$ we find $x = 5461$ , etc.

Therefore the general solution to this problem is the largest available number that may be written in the form $\tfrac13(4^n - 1) + 1$ , or $\tfrac13(4^n + 2)$ .

Alternative approach

Divide the sequence into blocks of four numbers. Thus, block # $k$ consists of the numbers $4k-3, \dots, 4k$ .

Of each block, only the second number survives, i.e. $4k - 2$ .

After steps 1 and 2, the surviving number of the $k$ th original block is now the $k$ th number. Therefore, if a number has position $k_n$ after $n$ steps, its position after $n-1$ steps must satisfy $k_{n-1} = 4k_n - 2$ . Definition $x_a := k_{n-a}$ , this becomes $x_{a+1} = 4x_a - 2.$

At the end of the process ( $n$ repetitions) we have one number left, in the first position, i.e. $k_n = x_0 = 1$ . Work backward to find the original position $k_0 = x_n$ : $\begin{array}{ccccccccc} a & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline x_a & 1 & 2 & 6 & 22 & 86 & 342 & 1366 & 5462 & 21\:846 \end{array}$

Since we started with numbers up to $12\:345$ , the process must end after seven steps at $k_0 = k_{n - 7} = \boxed{5462}$ .

Or , to generalize further, we can find an explicit expression for $x_a$ . The recursion $x_{a+1} = 4x_a - 2$ clearly describes exponential growth, but we must account for the term $-2$ . The trick is to rewrite it as $x_{a+1} - \tfrac23 = 4(x_a - \tfrac23).$ The solution of this recursion is $x_a - \tfrac23 = (x_0 - \tfrac23)\cdot 4^a,$ or $x_a = \frac{4^a + 2}3.$ Substituting $a = 7$ gives indeed $x_7 = \frac{4^7 + 2}3 = \frac{16\:384 + 2}3 = \boxed{5462}.$

In general, if the original series contains the numbers $1, \dots, N$ , then the remaining number is $\frac{4^{\lfloor \log_4 (3N-2) \rfloor} + 2}3.$

$\begin{aligned} \text {The starting number (head) of the 1st list is 1, where the list} &= [ 1,2,3,4, ..., 12345] \\ \text {The starting number (head) of the 2nd list is 2, where the list} &= [ 2,4,6,8,..., 12344] \\ \text {The starting number (head) of the 3rd list is 6, where the list} &= [ 6,10,14,..., 12344] \\ \\ \end{aligned}$ $\text {or in genral the value of head of the list after K iterations will be } head(K) = \dfrac{(4^K + 2)}{3} ....... (1)$

A list with $head(n) \gt 12345$ will be empty this $\implies$ that the answer is max $(head(n))$ where $head(n) \le12345$

$\displaystyle \text {Let N be the value of n that satisfies equation,} \\ \text {Let S to be the upper bound of the range} s = 12345 \ \ \text{in this case}$

Solving equation (1) gives $N = {\lfloor log_4(3S - 2) \rfloor }$

the general answer is $head = \Large{\lfloor \frac {(4^N + 2)}{ 3 } \rfloor}$

In this problem $S = 12345 \implies N = 7$

$\begin{aligned} h(N) &= \dfrac{(4 ^N + 2) }{ 3 } = \dfrac{(4 ^ 7+ 2)} {3} = \dfrac{ ( 16384 + 2) }{3} = \dfrac{16386}{ 3}\\ \\ &= \Large 5462 \\ \end{aligned}$

Write the numbers in base 4. Initially: 1, 2, 3, 10, 11, 12, 13, 20,...

After removing the numbers in odd position: 2, 10, 12, 20, 22, 30, 32, 100,...

After removing the numbers now in even position: 2, 12, 22, 32, 102, 112, 122, 132,...

We have left the numbers ending with 2.

After removing the numbers now in odd position: 12, 32, 112, 132, 212, 232, 312, 332,...

After removing the numbers now in even position: 12, 112, 212, 312, 1012, 1112, 1212, 1312,...

All numbers ending with 12.

Continuing in this way, it's obvious that the smallest remaining number at each cycle follows the pattern 2, 12, 112, 1112,....

The answer is thus the largest number in this sequence not greater than 12345 decimal, namely $1111112_4 = \boxed{5462}_{10}$ .

A recursive Python solution (a bit simpler than the others), which uses Extended Slicing :

1
2

f = lambda l, i = 1: f(l[i :: 2], 0 ** i) if l[1:] else l[0]
print(f(list(range(1, 12346))))

Prints the correct result, 5462 . Test it online!

Each step the count of the numbers is halved (rounding down on odd turns and up on even turns.) On even turns, the lowest number remains the same (because it isn't removed.) On odd turns, the lowest number becomes the next number (the lowest number + the step.) On each turn the step between the consecutive values doubles.

If you don't want to do math, make a computer do it for you.

1
2
3
4
5
6
7

a = list(range(1, 12346)) # produces a list of integers between 1 and 12345

while len(a) > 1:
    del a[0::2] # deletes elements in steps of 2 starting from index 0
    del a[1::2] # deletes elements in steps of 2 starting from index 1

print(a) # output is [5462]

After the first 2 steps, the remaining numbers are:

2, 6, 10, 14, 18, 22, 26, 30, ... ( the difference between the numbers is 4)

After 2 more steps the numbers remaining are:

6, 22, 38, 50, ... ( the difference between these numbers is 4x4= 16)

After the next 2 steps, we get:

22, 86, 150,...( the difference is 16x4= 64)

After 2 more steps, we get:

86, 342, 598,... ( difference of 64x4=256)

342, 1366, 2390,... (difference is 256x4= 1024)

1366, 5462, 9558 (difference 1024x4=4096)

The number after 9558 exceeds 12345. ( 9558+4096=13654)

In the next step, the numbers in the odd positions have to be removed. Hence, the answer is 5462

I am not good in mathematics so this is my approach programmatically:

Array starts as [ i ] where i spans from 1 to 12345 First Value: F=1 Spacing: S=1 [1,2,3,......]

Removing odd index causes second value to get to index of first and spacing doubled

F=2, S=2, array=[2,4,6,8......]

Removing even numbers doesn't change First Value while doubling the spacing

F=2, S=4, array=[2,6,10,14......]

Combining the 2 operations above, we know that after each round of taking away odd then even indexes:

F=F+S as value from second index replaces the first

S=S*4 as each operation to remove odd and even index doubles the spaces between the numbers in the array

Starting from F=1,S=1:

F=1,S=1

F=2, S=4

F=6, S=16

F=22, S=64

F=86, S=256

F=342, S=1024

F=1366, S=4096

F=5462, S=8192 <--- Answer

F=13654,S=32768

A short Python3 program that executes the algorithm :

1
2
3
4
5

l = list(range(1, 12346))
while len(l) > 1:
    l = l[1::2]
    l = l[::2]
print(l)

• If $n \in \mathbb{N}$ , then the number of steps required to find the winning number is $m$ , where $2^{m-1} < n < 2^m$ .
• After Step i is performed, the remaining numbers are of the form $2^{i-1}x + \frac{4^{k_i} + 2}{3}$ , where $x \in \mathbb{N} \cup \{0\}$ and $k_i = \lfloor \log_4(3.2^i - 2) \rfloor$
• The winning number can be found when $i = m$ and $x = 0$ , and that number is $\frac{4^{k_m} + 2}{3}$
• Now if $n = 12345$ , note that $2^{13} < n < 2^{14}$ so that $m = 14$ and $k_m = 7$ . Therefore, the winning number is $\frac{4^7 + 2}{3} = 5462$

Here is my solution, with basic Python 3 functions. The following code could be written in a more pythonic way, but I will keep it simple for all the begginers out there.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

num = list(range(1, 12346))


def t(n):
    do = []
    de = []
    for k in range(0, len(n), 2):
        do.extend([k])
    for i in reversed(do):
        del(n[i])
    for l in range(1, len(n), 2):
        de.extend([l])
    for j in reversed(de):
        del(n[j])


while len(num)!=1:
    t(num)
print(num)

I cheated a little lol. I used c++. Try it here (https://www.onlinegdb.com/online c++ compiler), replace everything already in the box:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

\#include <stdio.h>

\#define MAX 12345

int main() {

    int myArr[MAX];

    for (int i = 1; i <= MAX; i++) {
        myArr[i-1] = i;
    }

    int lastNumFlipped = 1;
    bool workLeft = true;
    bool killOdd = true;
    while (workLeft) {
        workLeft = false;
        bool odd = true;

        for (int i = 0; i < MAX; i++) {

            if (myArr[i] != 0) {
                workLeft = true;

                if (odd && killOdd) {
                    lastNumFlipped = myArr[i];
                    myArr[i] = 0;
                }
                if (!odd && !killOdd) {
                    lastNumFlipped = myArr[i];
                    myArr[i] = 0;
                }

            odd = !odd;    
            }
        }
        killOdd = !killOdd;
    }

    printf("Last Num Left: %i\n", lastNumFlipped);
    return 0;
} 

after 2 turns (that is step1 and step2), a sort of compression is performed: $m(x)=x/4+1/2$ we can ignore the decimal results, for example after the first 2 turns $m$ maps 2+4q into q

compounding m, I can write $m^{(k)}(x) = m(...m(x))$ (k-times)

I found $m^{(k)}(x) = i/4^k + \frac{4^k-1}{3*2^{2k-1}}$

$log_{4}(12345)=6.7...$ so I expect after applying $m^6$ to find at most 3 integer remaining values, solution of $m^{(6)}(x) = 1, 2, 3$

because step 1 has to be performed the solution has to be the second (unless the second value is bigger than 12345)

$m^{(6)}(x)=2$

$x=(2-\frac{4^6-1}{3*2^{2*6-1}})*4^6=5462$ that is a valid solution being less then 12345

My python solution:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def main(n):
    l = list(range(1,n))
    while True:
        l = l[1::2] 
        l = l[0::2]
        if len(l)==1:
            break
    return l

if __name__ == '__main__':
    print(main(12345))

in Javascript (ES6)

let arr = new Array(12345).fill(0).map((d,i) => i+1 );
while (arr.length > 1) {
  arr = arr
    .filter((d,i) => (i+1) % 2 === 0)
    .filter((d,i) => (i+1) % 2 !== 0);
}
console.log(arr[0]);

At the beginning, it's clear that every number equals it's position.

After the first step, only even numbers remain, and it can easily be seen that now every number equals twice it's position, satisfying the equation $x = 2n$ , where x equals the number and n equals the new position.

After the second step, every number in an even position is eliminated. If we write a few of the numbers remaining: $2, 6, 10, 14, 18, 22, ...$ , we can see they produce an arithmetic sequence with difference(d) 4, and that $x \equiv 2 \equiv -2 \pmod{4}$ , such that now $x = 4n - 2$ , where n is the new position.

If we do the first step (so that this is the third step) again, we'll eliminate numbers in odd positions, and as odd positions occur every two number, and before d = 4, now d will become 8, and the sequence will look like these: $6, 14, 22, 30, 38, 46, 54, ...$ and we can see that now, $x = 8n - 2$ . We can continue doing this, and finding a formula for x after each step, and find a pattern in the formulas that will lead us to a generalization:

4^{th} step: $6, 22, 38, 54, 70, ...$ . Formula: $x = 16n - 10$ 5^{th} step: $22, 54, 86, 118, 150, ...$ . Formula: $x = 32n - 10$ 6^{th} step: $22, 86, 150, 214, 278, ...$ Formula: $x = 64n - 42$

Now, I hope it'll be easy to verify, that the general formula is (for $s \geq 2$ ): $x = 2^sn - \sum_{i=1}^{\left \lfloor{\frac{s}{2}}\right \rfloor} 2^{2i-1}$ , where s equals the step, and n the position.

If someone can find a better general formula, please write it in the comments.

Since the difference in an arithmetic sequence with the remaining numbers (in order) after step s equals $2^s$ , and $2^13 < 12345 < 2^14$ , we should check, with the general formula, n = 1 and s = 13 or s = 14. These give respectively 5462 and 5462, because in s = 14 we eliminate numbers in even positions, and 5462, at s = 13 , is in an odd position. If we plug in n = 2, for each of them, we get 13654 and 21846, both bigger than 12345, so we can be sure that the last "survivor" from 1 to 12345 is:

$\boxed{5462}$

Footnote: I know this is far from being a rigorous solution, but actually i'm not very good at writing solutions, so that if I were to try and prove this way of solving the problem, the solution would become large and difficult to read. I will appreciate if you could give me advice on how to write good and clean solutions down here in the comments.

Here is mathematical solution to the problem and an implementation in program code.

THOUGHTS ABOUT SOLUTION WITH CODE

There is such a thing as getting the answer without solving the problem. Emulating the described steps as a brute force "solution" in code is an example.

Applying the mathematical result and some programming technique produces code that uses minimal resources in both time and space (without arrays or recursion stack) that are fixed regardless of list length, and can be optimized by replacing floating point calculations with pure fixed point operations. This lends some depth to the programming side of the solution. The brute force step emulation examples regardless of number of lines of code used all negate the value of the problem both as a math exercise and a programming exercise. That is the objection to most if not all of the program code "solutions".

SOLUTION

There is a definite sequence of "last numbers". The solution is the greatest "last number" less than the greatest number on the list.

The last number for any list 1..n is given by:

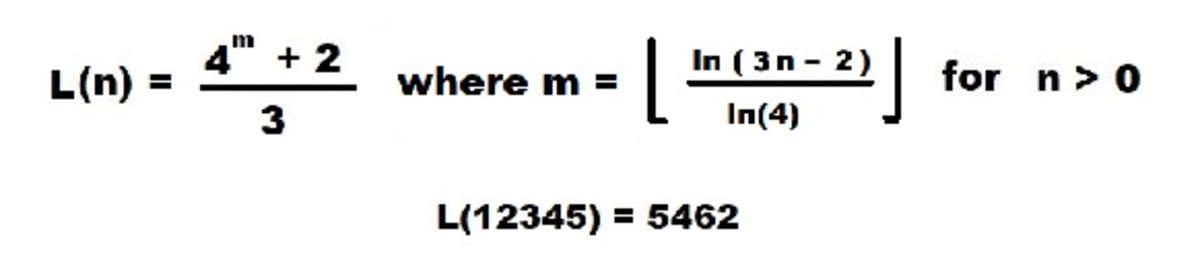
This can be established as follows:

The key fact is that next position from any given position, p, is $N(p) = \lceil { \frac{p}{2} \rceil }$ (least integer greater than p/2)

The function $N()$ is strictly decreasing until $N(p) = 1$ when $N(1) = 1$ . Thus every number not eliminated by parity will eventually reach position 1 when it will be either the last number or be eliminated on the next odd eliminating step. While it is true that $N(2k) = N(2k-1)$ it is not a problem because either $2k$ or $2k-1$ will have been eliminated on parity, to bring the surviving number uniquely to the new position.

What is of interest here is the inverse of $N()$ which is not a function. $N()$ . Any given position p can only come from one of two prior positions, 2p or 2p-1. The choice of precursor is entirely forced by the type of step, i.e. if the previous step eliminated odd positions, the precursor must be 2p, and if eliminating even positions must be 2p-1.

The last number will be in position 1, the only position remaining. If the current step is odd, then the previous position must have been 1 (not eliminated on an even eliminating step). If the current step is even, then the previous position must have been 2 (not eliminated on an odd eliminating step).

With that logic in hand, the full sequence of last numbers, ${ L_m }$ can be generated uniquely starting from 1 on an odd eliminating step.

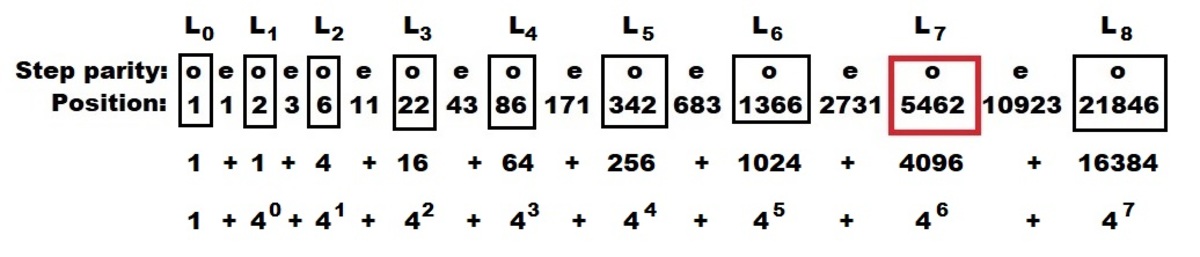
The difference between successive odd steps increases by a factor of 4 can be seen by examining the value of $N(p)$ across successive odd eliminating steps as follows:

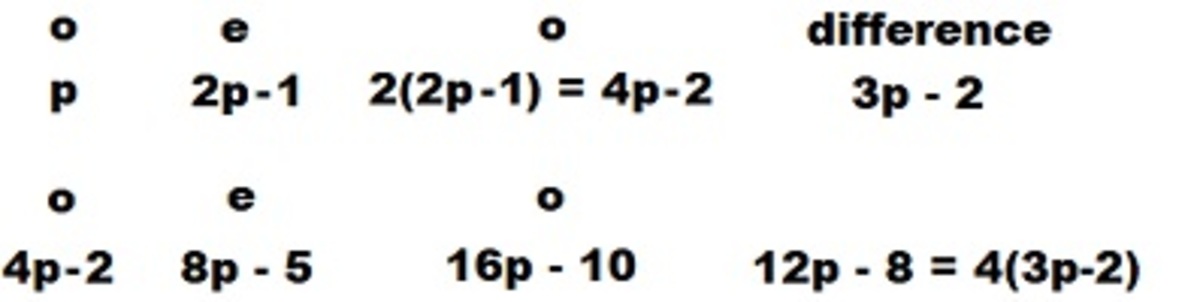
The solution to the problem is the greatest ${ L_m }$ that is less than the highest position in the initial list (since the last number must be on the list in the first place). We can disregard the intermediate odd numbers in the sequence above because they are all eliminated on the first step.

The sums of powers of 4, can be calculated directly using the formula for geometric sums.

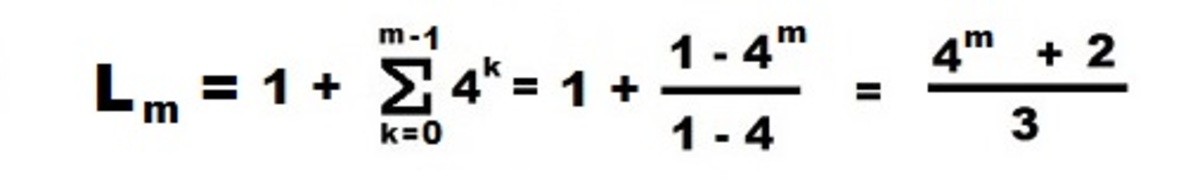
From that a general solution is expressed by

The value of m can be obtained directly as follows.

Taking the base 4 logarithm With the value of $log_4 ( \frac{3n - 2}{3 })$ between two consecutive integers, and a change of base, it follows that

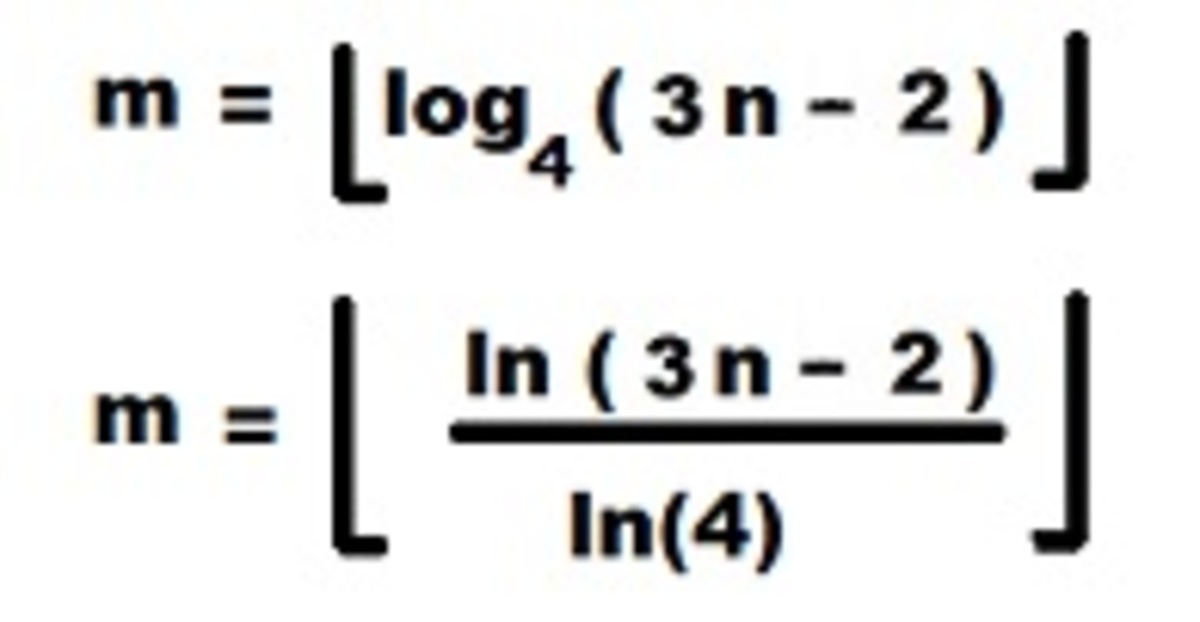
Which completes the derivation of the function $L(n)$ given at the top of the page.

The value marked in red 5462 is the value of $L(12345)$ and the solution to the given problem.

In the example given with the problem, we see that $L(8) = 6$ , since ${ L_{2} }$ = 6 < 8 and ${ L_{3} }$ = 22 > 8.

SOFTWARE IMPLEMENTATION

Using the math the resulting code uses fixed resources in both instructions executed and memory used (both minimal without any arrays nor recursion stack ) regardless of the length of the list This is an improvement over the brute force approach that literally performs the elimination step process, both as use of the problem as math exercise and as a programming exercise.

Below is the solution implemented as program code { In Excel VBA for convenience not preference ).

This subroutine implements the solution in the mathematical form derived above

These subroutines implement the solution optimized by the use of right shift pseudo-division to obtain the exponent of 4.

Using a User Form container with a command button.

The code above is executed

Another python code

a = list(range(1,12346))
b = []
c=[]

while len(a)>1:
    i=0
    j=0
    for n in a:
        if j%2==1:
            b.append(n)
        j+=1

    for n in b:
        if i%2==0:
            c.append(n)
        i+=1        
    a = c
    b=[]
    c=[]


print(a)