Four Touching Circles

You can form a square with the radii of the circles, using the centers as corners. If each radius is 8m, then each side of the square is equal to 16m.

Area of square = ${ 16 }^{ 2 }= 256$

Then, as we can tell from the newly created square, each blue section of the circle is $\frac{1}{4}$ of the original circle. Since there are four of these sections inside the square, we have a full circle inside that consists of all the non-shaded area.

Area of circle = $\pi { r }^{ 2 }= { 8 }^{ 2 }\pi = 64\pi$

So, the area of the red region is $256 - 64\pi.$

If you connect the centre of the circles you will have a square, which has area $16^2 = 256.$

Then, the blue area of each circle is 1/4 of the circle, or $\frac{1}{4} \cdot \pi \cdot 8^2 = 16\pi.$ So all of the circles combined have area $64\pi.$

Thus, the red area is $256-64\pi.$

just focus on one circle... make an imaginary square around it. By inspection, the Area outside the circle but inside the square is just equal to the shaded area you are looking for. to solve. first, we must find the area of the square(As) which is As= (8+8)^2 = 256. second, we must find the the area of the circle (Ac) which is Ac= 3.142 X 8^2 = 201.088 Lastly, subtract the area of the square to the area of the circle. As-Ac = 256- 201. 088 = 54. 912 .

– Consider a square through centers of 4 circles. Required area is Area of square – 4 quarter circles = (2 r)^2 – pi r^2 = r^2 (4 – pi) = 54.9 m^2

Join the centres of the circles to firm a square of side 16 units. Required area equals (area of square)-4*(area of one quadrant)

solve for the area of the sector of one blue circle... A(sec) = 1/2 radius^2 (pi/2) = 1/2 8^2 (pi/2) = 1/2 64 1.5708 = 50.2656 sq m

then solve for the area of the square... A(sq) = 8^2 = 64 sq m

then, A(red) = 4 (A(sq)-A(sec)) = 4 (64-50.2656) A(red) = 54.9376 sq m (ans)

can you pls post more questions like this?

If we join centres of all circles,we get a squarehaving each side 16 cm and 4 quadrant circle with red portion inside of quadrant.rea of square is 16 x 16 =256 and all 4 quadrant of circle of radius 8.Area of circles will be pi x r sqare that is 3.14 X 64 = 200.96 cm2. now ,subtracting yhis from 256 we get area of red square = 54.94 Ans K.K.GARg,India

To make it much more clear.. As someone earlier in the comments mentioned, a square can be formed by joining the centres of circles. Each side of square becomes 16,hence area of square formed will be 16x16=256! Out of which the blue portion inscribed in the square should be subtracted. Area of each circle will be πr² and for four circles and 1/4th part of it we get 4 (1/4) πr² Resulting in the Area of highlighted portion- 256-π(8)²=54.94 units.

256-64pie=54.94

Percebam que a área formada pelos 4 pontos forma um quadrado de aresta 16, portanto, uma área de 256. Se somarmos a área dos 4 um quarto da circunferência, obteremos área de uma delas usando Pi. R2. cujo raio é 8 metros. dessa forma, subtraindo a Área da circunf. do total do quadrado formado pelos pontos tem-se o valor de 54,94.

Required area = area of square whose half side is equal to the radius of circle- area of complete circle ( since 4 quarter part of circle makes up a cirle=16 (16)- 3.14 (8) (8)=54.94

the red part is simply the outside of single blue circle inscribed in a square

the area of the square = 16x16 = 256

the area outside the circle is the area of square - area of circle

or this can be in a simple proportion of

[(4 - 3.141592)/4] (area of square)

(0.858408/4) (256) = 54.938

actually it should be 54.93

First of all connect those 4 dots (which is origin of circles) in your mind making it a square.

It is given that radius of each circle is 8 meters. Hence each side of the square will be 8 + 8 = 16 meters.

Area of that square will be ${ 16 }^{ 2 }$ = 256.

Now we have to find area of sector of circle with 90 degree of angle. (We have to take 90 degree because we formed a square from the origins of all of the circles.)

Area of Sector

= ½ × (θ × π/180) × r^2   (where θ will be in degree)

= ½ × (90 × 3.142/180) × 8^2 = 50.27

Multiply it with 4 since we have 4 circles. = 50.27 × 4 = 201.088.

Now just deduct area of sectors from area of square. = 256 - 201.088 = 54.912 is correct answer.

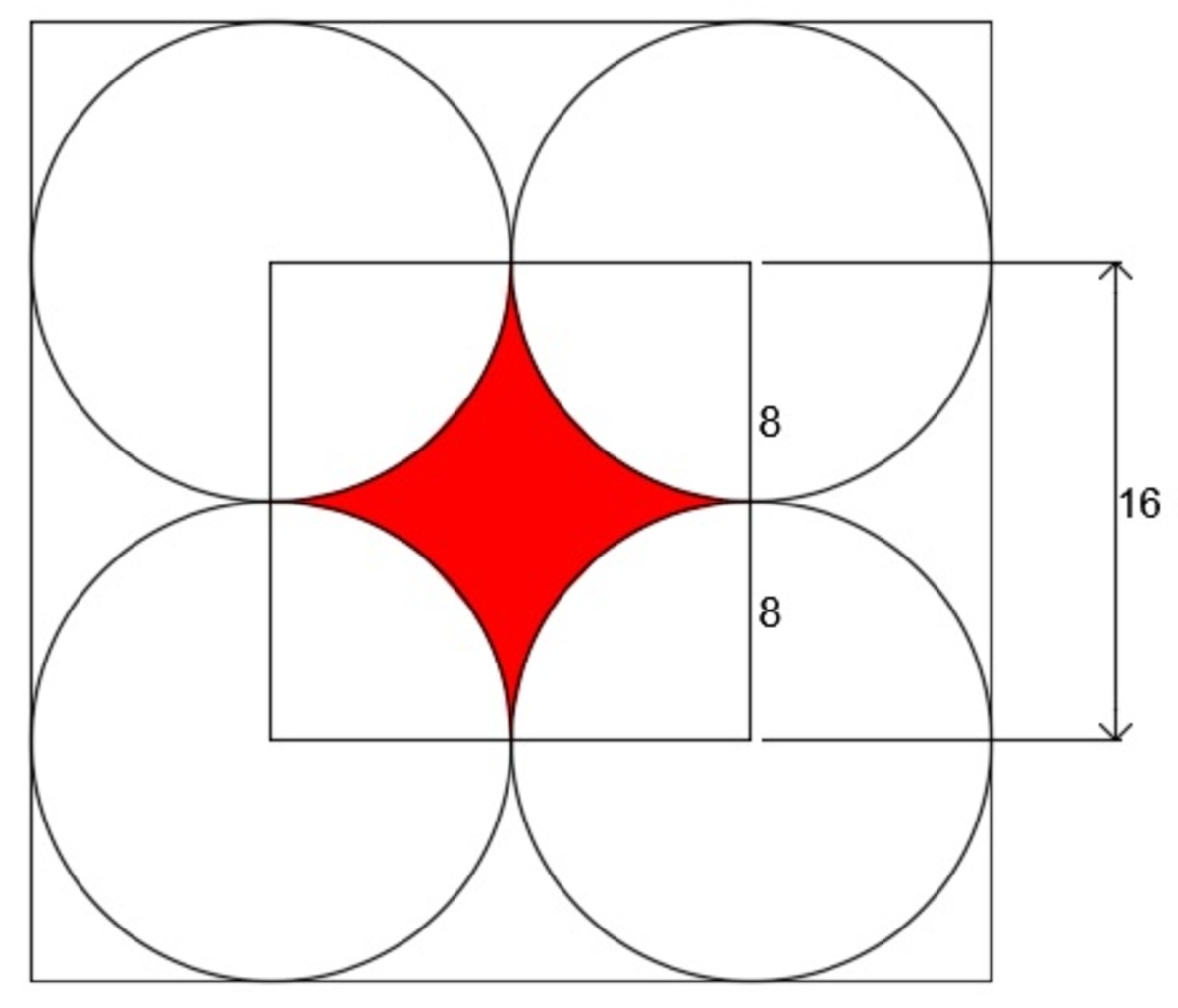Connect the centers of the circles to form a square with side length of 16. The area of the red region is equal to the area of the square minus the area of four quarter circles (which is also equivalent to one circle). So the desired area is

area of red region = area of square - area of circle

area of red region = 16² - pi * 8² = 256 - 64pi

Answer: 256 - 64 * pi

256-201.09 = 54.91

area of the highlighted part is equal to the area of the square minus the area of a single circle

square is the connection of the 4 centers of the circles

First take center of all 4 circles which will make square of area 16 16=256 Then minus the area of all circles one fourth make one circle .... 256-(π 16*16/4)= 54.91