Oddly defined triangle (2)

If we shift the coordinate system so that the circumcentre $\Gamma$ is at the origin, then $A$ has coordinates $(5,12)$ and the orthocentre $O$ has coordinates $(6,9)$ . If the position vectors of $A,B,C$ relative to the origin $\Gamma$ are $\mathbf{a},\mathbf{b},\mathbf{c}$ , then we have $\mathbf{a} \; = \; \left(\begin{array}{c} 5 \\ 12 \end{array}\right) \hspace{2cm} \mathbf{a}+\mathbf{b} + \mathbf{c} \; = \; \left(\begin{array}{c} 6 \\ 9 \end{array}\right)$ Note that the circumradius is $R = 13$ and that $\mathbf{b} + \mathbf{c} \; = \; \left(\begin{array}{c} 1 \\ -3 \end{array} \right)$ Moreover $\mathbf{c} - \mathbf{b}$ must be perpendicular to $\mathbf{b} + \mathbf{c}$ (since $\mathbf{b},\mathbf{c}$ both have length $13$ ), so must be parallel to $\binom{3}{1}$ . Thus we must have $\mathbf{b} \; = \; \left(\begin{array}{c}\tfrac12(1-3u) \\ -\tfrac12(3+u)\end{array}\right) \hspace{2cm} \mathbf{c} \; = \; \left(\begin{array}{c} \tfrac12(1+3u) \\ \tfrac12(u-3)\end{array} \right)$ for some $u$ . Since $\mathbf{b}$ has length $13$ , we deduce that $169 \; = \; \tfrac14(1-3u)^2 + \tfrac14(3+u)^2 \; = \; \tfrac{5}{2}(u^2 + 1)$ and so that $u = 3\sqrt{\tfrac{37}{5}}$ . Since $\mathbf{a} - \mathbf{b} \; = \; \left(\begin{array}{c}\tfrac12(9 + 3u) \\ \tfrac12(27 + u)\end{array}\right)$ we deduce that $AB^2 \; = \; \tfrac14(9 + 3u)^2 + \tfrac14(27 + u)^2 \; = \; \tfrac52(u^2 + 81) + 27u \; = \; 369 + 27u$ and similarly $AC^2 \; = \; 369 - 27u$ Also $\mathbf{c} - \mathbf{b} \; = \; \left(\begin{array}{c} 3u \\ u \end{array}\right)$ and hence $BC^2 \; = \; 10u^2$ Thus $P \; = \; \sqrt{369 + 27u} + \sqrt{369 - 27u} + u\sqrt{10} \; = \; 62.27584442$ making the answer $\lfloor P \rfloor = \boxed{62}$ .

With an orthocenter at $(3,3)$ and a circumcenter at $(-3,-6), \ \triangle ABC$ has a centroid at $(-1,-3)$ . The line that passes through $A$ and $O$ has equation $y = -3x + 12$ . Since this line is perpendicular to $\overline{BC}, \ \overline{BC}$ has a slope of $\dfrac{1}{3}$ .

Let the centroid of the triangle be denoted by $\Phi$ . The line containing $\overline{A\Phi}$ has equation $y = 3x$ . Since this line passes through vertex $A$ , it must also pass through the midpoint of $\overline{BC}$ ( $\overline{A\Phi}$ is a median).

Note that the circumcenter lies on the perpendicular bisector of $\overline{BC}$ so the line that passes through the circumcenter of $\triangle ABC$ and the midpoint of $\overline{BC}$ is also perpendicular to $\overline{BC}$ , giving it the same slope as $\overline{AO}$ . Hence, it has equation $y = -3x-15$ .

The perpendicular bisector of $\overline{BC}$ and the median through vertex $A$ meet at the midpoint of $\overline{BC}$ . Hence, $-3x-15 = 3x \implies x = -\dfrac{5}{2}$ . Therefore, the equation of the line containing $\overline{BC}$ is thus $y = \dfrac{1}{3} \left( x - 20 \right)$ . Checking the points where this line intersects the circumcircle yields: $\left( x+3 \right)^2 + \left( y+6 \right)^2 = 169 \implies \left( x+3 \right)^2 + \left( \dfrac{x-20}{3}+6 \right)^2 = 169.$ Expanding the equation above and completing the square yields

$x \in \left\{ -\dfrac{5+9\sqrt{\dfrac{37}{5}}}{2}, \dfrac{9\sqrt{\dfrac{37}{5}}-5}{2}\right\}$ which when used in equation $y = \dfrac{1}{3}\left( x-20 \right)$ shows that the coordinates of vertices $B$ and $C$ are

$\left(-\dfrac{5+9\sqrt{\dfrac{37}{5}}}{2}, -\dfrac{15+3\sqrt{\dfrac{37}{5}}}{2} \right) \ \text{ and } \ \left( \dfrac{9\sqrt{\dfrac{37}{5}}-5}{2}, \dfrac{3\sqrt{\dfrac{37}{5}}-15}{2} \right).$

Applying the distance formula to each pair of vertices gives the following approximate side lengths: $\left\{ 24.276, \ 25.807 , \ 12.192\right\}.$ Therefore, $P \approx 62.275$ , so $\left \lfloor P \right \rfloor = 62$ .

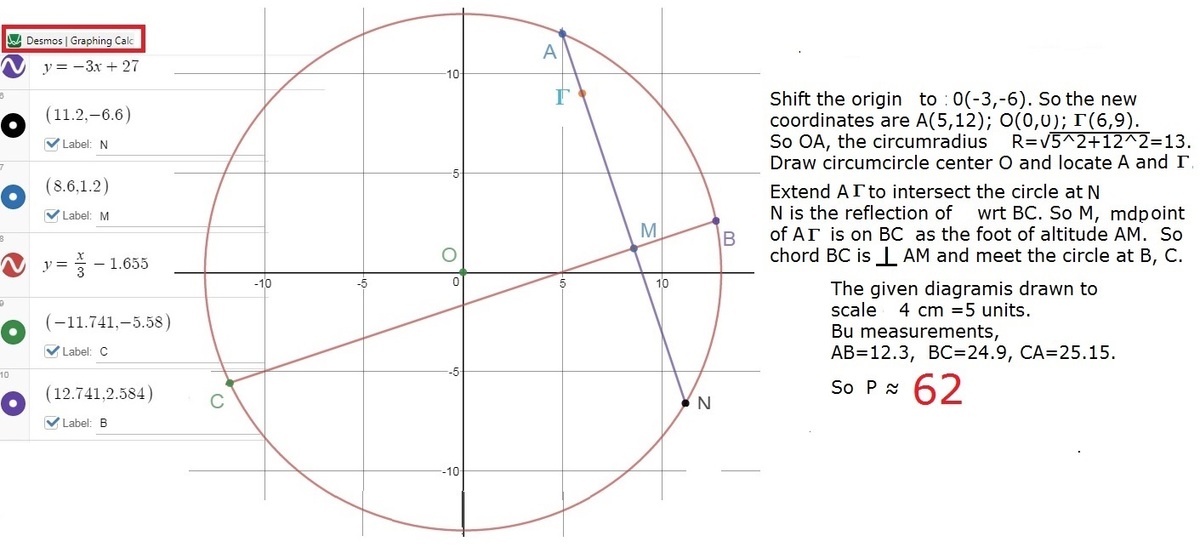
Above is the solution through geometric cunstraction to scale. Below is the analytical solution with the same logic.

$Change~ the~ x\!-\!y~ to~ X\!-\!Y~ with~ origin~ at~ O.~~ ~ So~ A(5,12),~~ O(0,0),~~ \Gamma(6,9).\\ Circumradius~R=\sqrt{5^2+12^2}~=13. ~~So ~circumcircle~is~~\color{#3D99F6}{X^2+Y^2=13^2}.\\ Altitude~AM~through~\Gamma,~~~~~Y=\dfrac{9-12}{6-5}*(X-6)+9. \implies~. ~\color{#3D99F6}{Y=-3X+27}.\\ Let~the~altitude~AM~intersect~the ~circle~at~N.\\ Then~Y_N=-3X_N+27~\cap~X^2+Y^2=13^2,~~~gives~N(11.2,-6.6).\\ Since~ N~ is~ the ~reflection~ of~ \Gamma ~about~ BC, \\ \therefore~ M,~ the~ midpoint~ of~ \Gamma N~ is~ the~ foot~ of~ altitude ~AM. \\ \therefore~chord~BC~is~one~side~of~\Delta~ABC.\\ BC ~\cap~ \bigcirc,~~ give~ C(-11.741, - 5-58),~B(12.741,~2.58).\\ Using~distance ~formula~P=62.275. ~\Large~~\color{#D61F06}{P\approx~62}.$