Oh my god!
Find the sum of the roots of the following equation.
x 8 0 6 1 + ( 2 1 − x ) 8 0 6 1 = 0
The answer is 2015.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I calculated the coefficient of x 8 0 6 1 and x 8 0 6 0 and x 8 0 5 9 in the expansion of ( 2 1 − x ) 8 0 6 1 and used Vieta to find the sum of the roots though I think your solution seems very elegant.
Hello,
Maybe I don't understand the question very well because I'm French, but this equation doesn't have any real root... x^8061=-(1/2-x)^8061 <=> x=-1/2+x <=> 0=-1/2 <=> S=0 => sum(x,xES)=sum(x,xE0)=0... isn't it?
Log in to reply
True, the roots will all be non-real!
But are we sure that the roots are simple roots?... because if not, if roots are roots of the derivative polynom, we don't have 8060 terms in the sum but less...................
Log in to reply
There are no multiple roots in this case... just take the derivative and solve the system f ( x ) = f ′ ( x ) = 0 .
When people ask for the sum of the roots of a polynomial, they usually mean the sum of the complex roots, counted with their multiplicities... maybe this should have been stated explicitly.
Log in to reply
OK... I didn't know for the multiplicitie count... Thanks.
Log in to reply
@Elden Knight – Well, there are no multiple roots, so, it's not really an issue here...
sir please elaborate
First, we can expand the given.
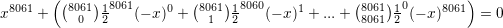
Then, simplify. (Note that
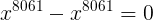 )
)
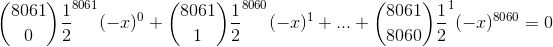
Using Vieta's Theorem, the sum of the roots is
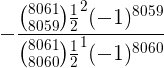
The sum of the roots of the original polynomial is
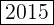 .
.
Did the same way.
Make a substitution x = y + 4 1 and write the equation as ( 4 1 + y ) 8 0 6 1 + ( 4 1 − y ) 8 0 6 1 = 0 . The sum of the roots of this even polynomial of degree 8060 is 0, so that the sum of the roots of the original polynomial is 4 8 0 6 0 = 2 0 1 5 .