Olympiad problem
( x + y + z ) 2 ( x 1 + y 1 + z 1 )
Given that 2 1 ≤ x , y , z ≤ 1 , find the sum of the minimum and maximum value of the expression above.
The answer is 40.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
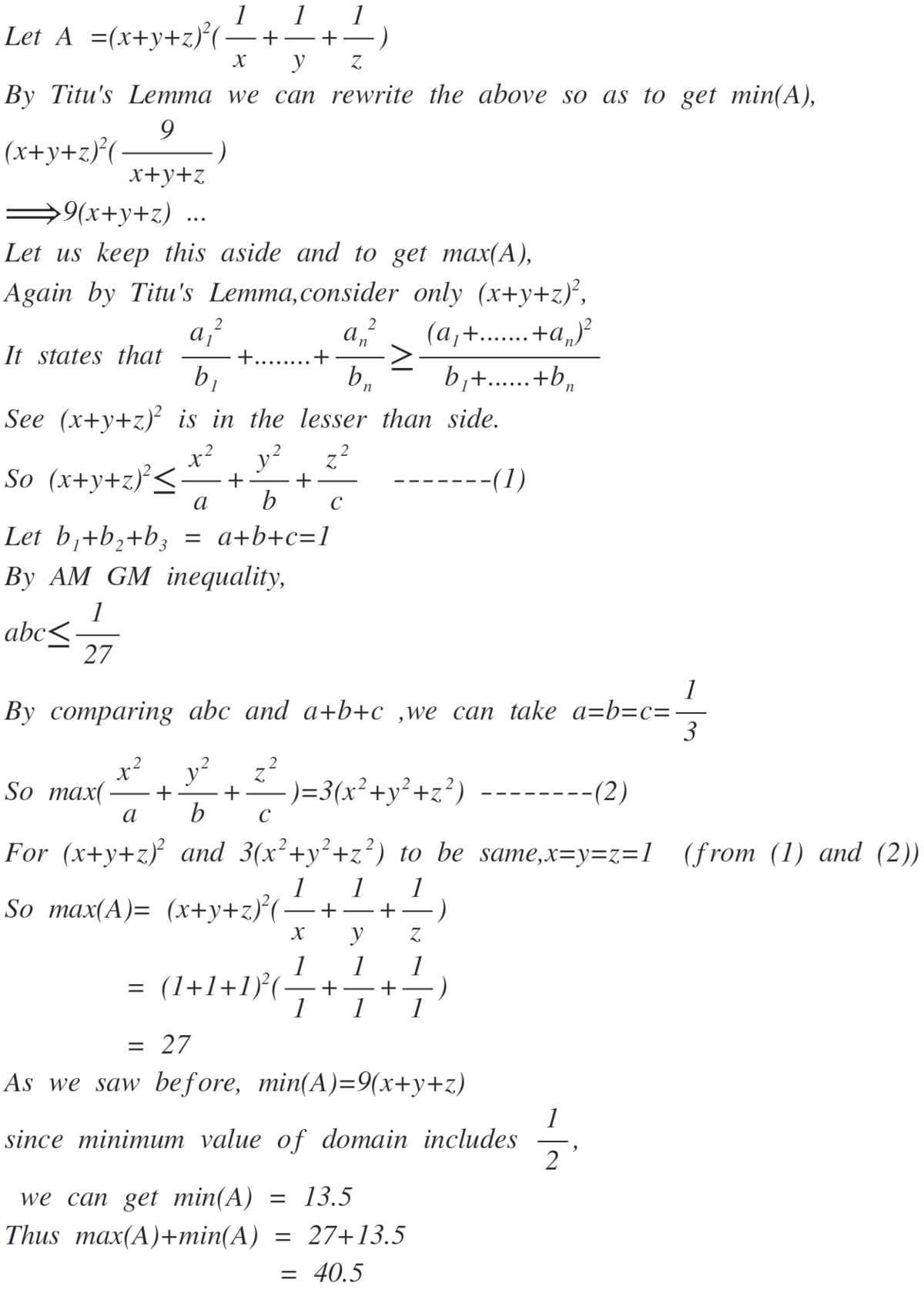 *
*
bold text
bold text
bold text
bold text
*
*
bold text
bold text
bold text
bold text
good solution...
Let the expression above be P .
By Cauchy-Schwarz inequality,
P = ( x + y + z ) ( x + y + z ) ( x 1 + y 1 + z 1 ) ≥ ( x + y + z ) ( 1 + 1 + 1 ) 2 = 9 ( x + y + z ) ≥ 2 2 7 .
We check that this minimum is attained when x = y = z = 2 1 .
Next, viewing the expression as a function in x (by writing C = y + z and D = y 1 + z 1 respectively) gives:
P = ( x + c ) 2 ( x 1 + D )
= D x 2 + ( 2 C D + 1 ) x + x C 2 + C 2 D + 2 C
Note that
P ′ ( x ) = 2 D x + 2 C D + 1 − x 2 C 2
P ′ ′ ( x ) = 2 D + x 3 2 C 2
Since all x , C and D are positive, P ′ ′ ( x ) > 0 , therefore P ( x ) is a convex function.
Viewing the expression as functions of y and z , we arrive at the similar conclusion that the expression is convex in terms of x , y and z . Since the maximum of a positive convex function is attained when all its variables are at the extremum of their respective domains. Checking the value of P when x , y , z ∈ { 2 1 , 1 } , we find that maximum is attained when x = y = z = 1 .
Upon some computation, the minimum is 2 2 7 while the maximum is 2 7 . Adding them up yields 4 0 . 5 , hence the answer.
Moderator note:
Can you spot your mistake? The following statement is not true.
Since the maximum of a positive convex function is attained when all its variables are at the extremum of their respective domains, we conclude that the maximum for P must either occur when x = y = z = 1 or x = y = z = 2 1 .
Nice solution ! By the way, which Olympiad is it from ?
Log in to reply
yeah,it is .but i'm not happy with the question
Log in to reply
Why ? What's wrong ?
Log in to reply
@Rohit Kumar – it's easier than I expect from a level 5 question
Log in to reply
@Sarith Imaduwage – Yeah , some problems are overrated. Ratings fluctuate.
Can you spot your mistake? The following statement is not true.
Since the maximum of a positive convex function is attained when all its variables are at the extremum of their respective domains, we conclude that the maximum for P must either occur when x = y = z = 1 or x = y = z = 2 1 .
Log in to reply
I think:
The maximum of a positive convex function is attained when all its variables are at the extremum of their respective domains
is correct.
However, I should check all cases for ( x , y , z ) = { 2 1 , 1 } . I am jumping too early to conclusion.
Log in to reply
Correct. There are 2 3 cases to check, not just 2.
Note that the equation should be x , y , z ∈ { 2 1 , 1 } , which means that "The variables x, y, z belong to the set 0.5, 1". Your equation currently does not make sense.