On the power of divisors

Number Theory Level 3

Let $N$ be a positive integer having at least 4 positive divisors.

Denote $d_1, d_2, d_3, d_4$ as the smallest positive divisors of $N$ .

Also, let $k\geq2$ be a positive integer such that $N=d_1 ^k + d_2 ^k + d_3 ^k + d_4 ^k$ .

If $q = 2^k + 1$ is a prime, what is $\mathcal v_q (N-q)$ ?

Note: $\mathcal v_p (n)$ denotes the largest power of $p$ dividing $n$ .

k-2

k-1

k

k + 1

k + 2

This is impossible, no such

N

exist

2 solutions

Srijan Bhowmick
Feb 21, 2021

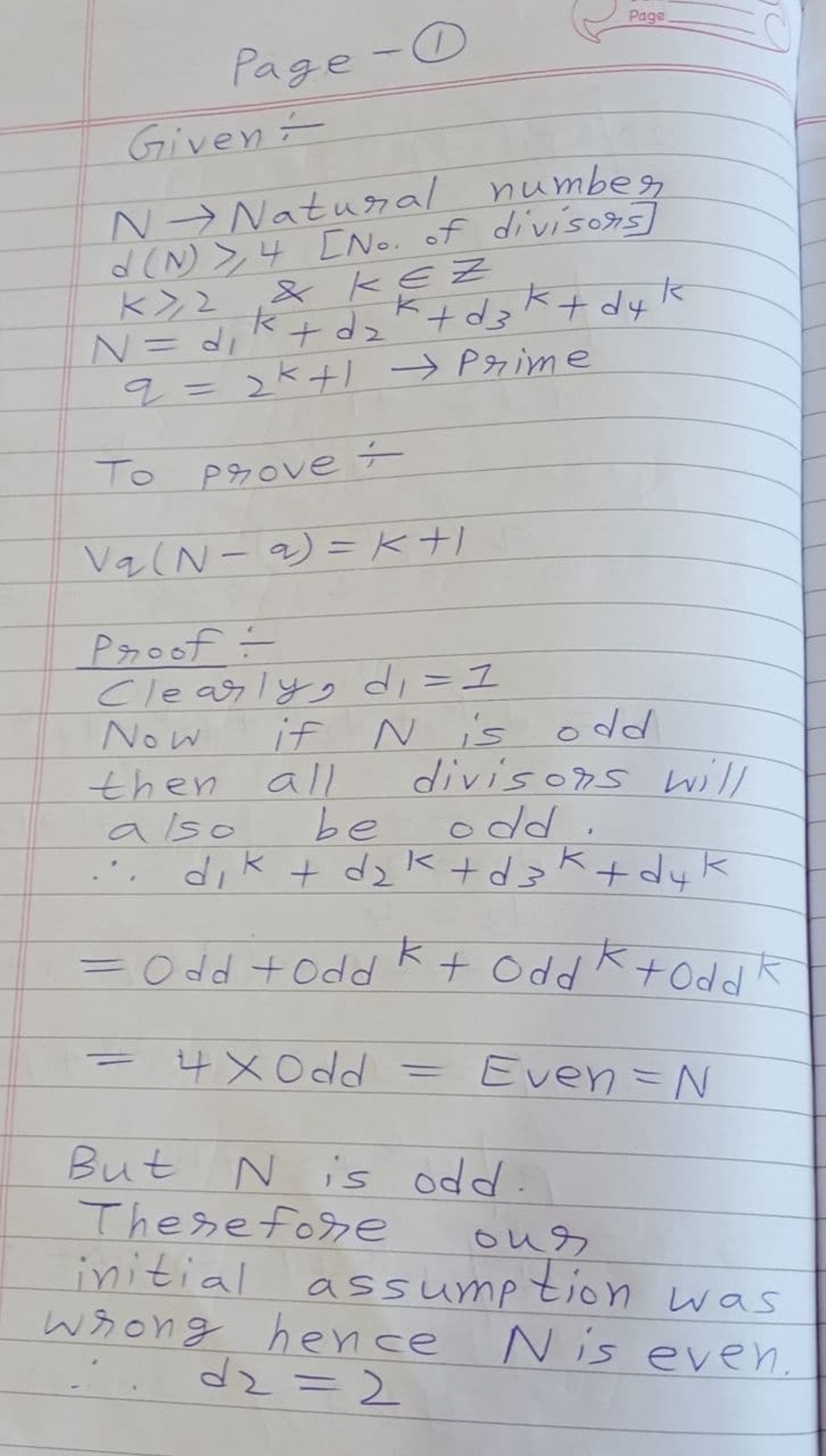
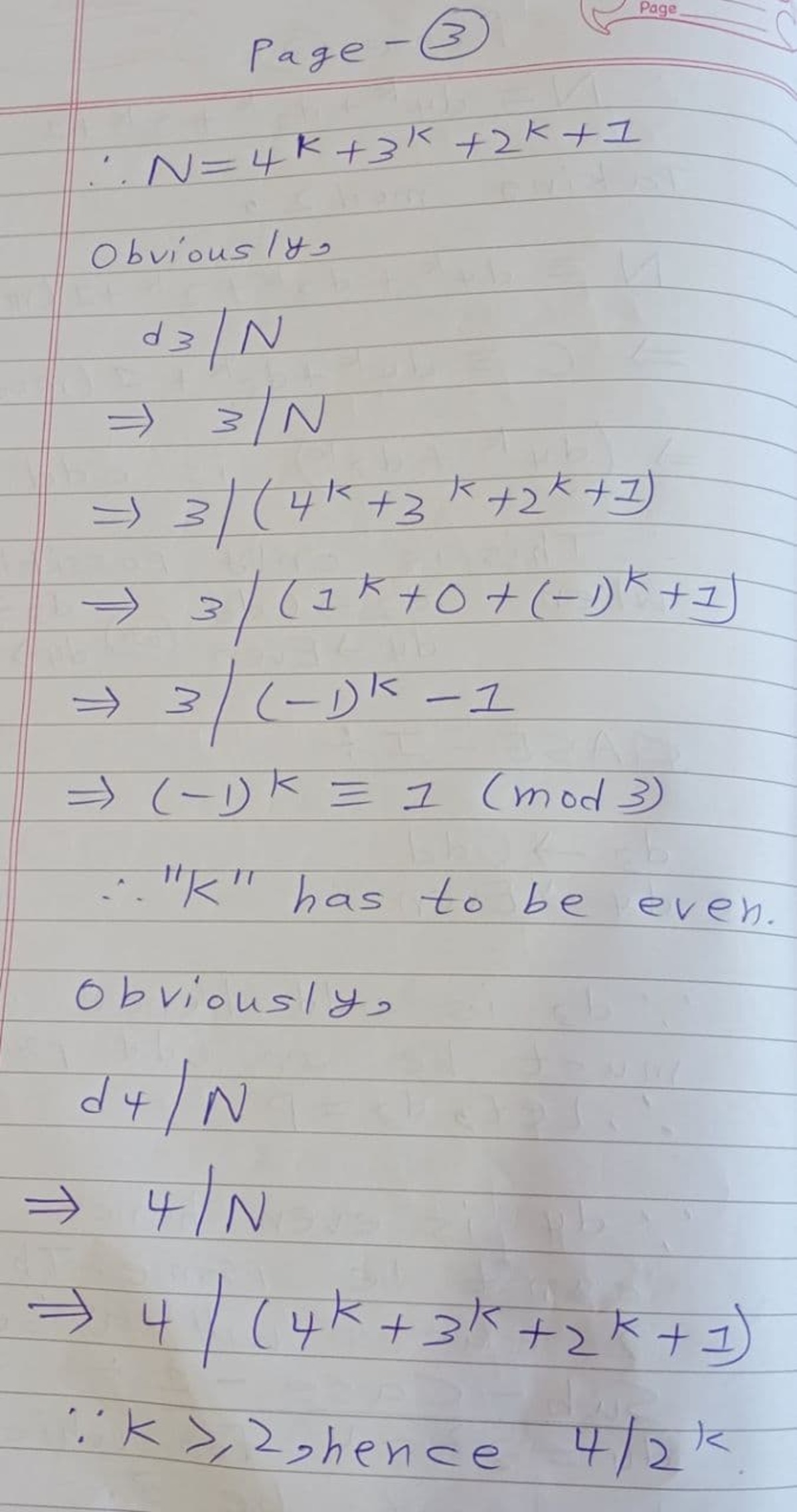
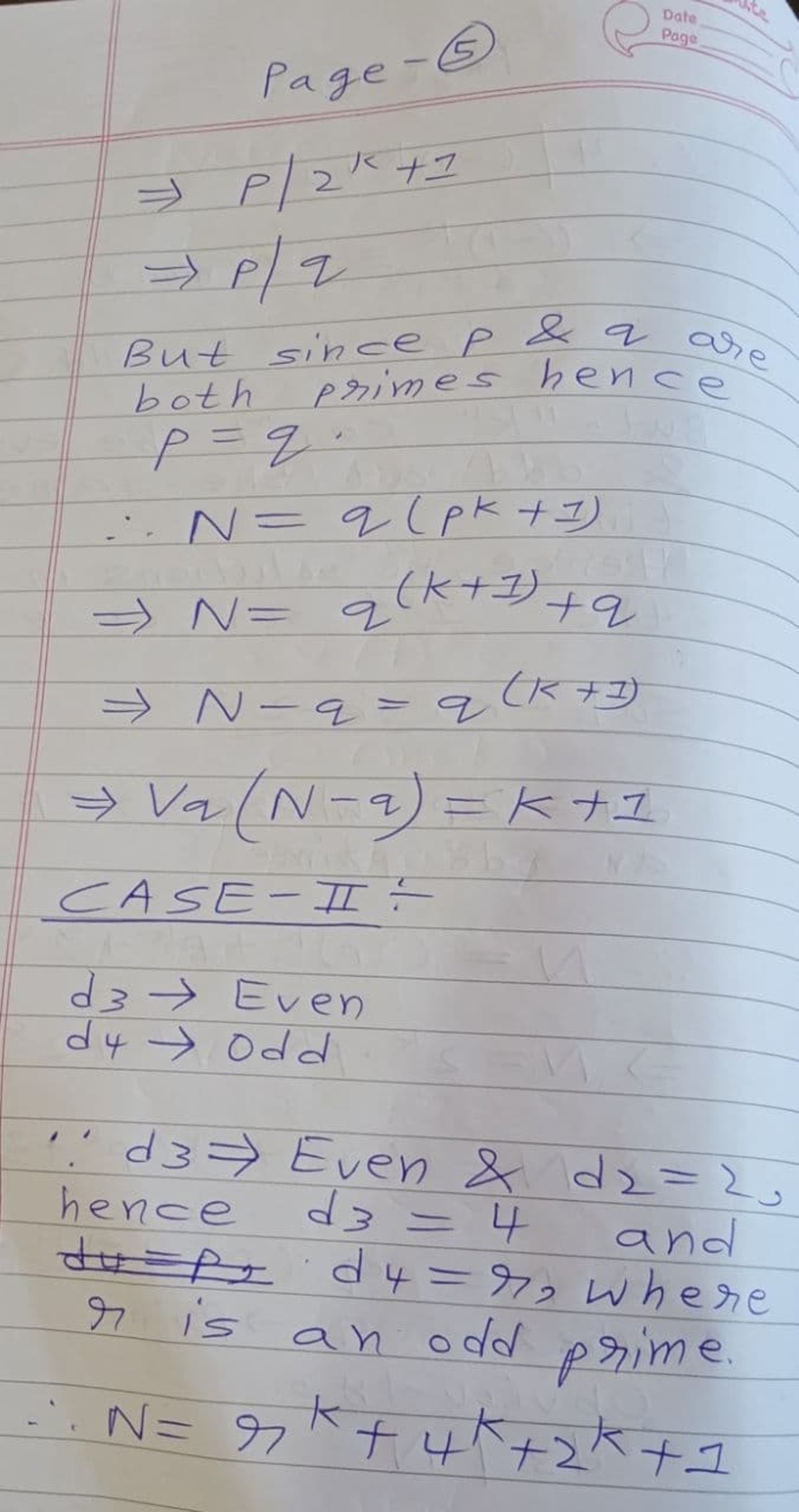
Fantastic work! Interesting problem and a really good write-up.

One thing that would make your final casework (Case II) a little shorter is to observe that if $k\ge 2$ and $q=2^k+1$ is prime, $k$ must be even (in fact, $k$ must be a power of $2$ ); for if not, then $k$ has an odd prime factor, say $P$ , and $q=2^{aP}+1=\left(2^a\right)^P+1$ which is divisible by $2^a+1$ (these are Fermat primes.)

As soon as you reach (in your solution) $r^k \equiv 3 \pmod4$ , you can stop, because this is impossible for even $k$ .

One other point is that solutions do exist - the smallest is $N=130$ ; the next, corresponding to $k=4$ , is $N=1419874$ .

Chris Lewis - 3 months, 2 weeks ago

Thank you for the compliment ! And I really liked your approach for Case - 2 And thanks for making me aware about Fermat primes 😀 And another thing , can you find an upper bound for the number of divisors of N ?

Srijan Bhowmick - 3 months, 2 weeks ago

That's an interesting followup. The lazy answer is "yes, sort of"; there are only four known Fermat primes, so there are only four known such $N$ , of which one will have the most divisors.

Interestingly, $k=8$ , $q=257$ doesn't work; the $N$ generated has another odd prime factor less than $257$ .

The other possibilities do all work; we have

$k$	$q$	$N$	Prime factorisation	# divisors
$2$	$5$	$130$	$2\cdot 5 \cdot 13$	$8$
$4$	$17$	$1419874$	$2\cdot 17 \cdot 41761$	$8$
$16$	$65537$	$\approx 7.6 \times 10^{81}$	$2\cdot65537\cdots$ ( $7$ prime factors)	$128$

So the largest number of divisors of the $N$ we know about is $128$ .

It's thought that $65537$ is the largest Fermat prime; but not yet proven, so there may be ridiculously big $N$ that work with perhaps more divisors.

Chris Lewis - 3 months, 2 weeks ago

@Chris Lewis – Interesting 🙃

Srijan Bhowmick - 3 months, 2 weeks ago

Mark Hennings
Feb 22, 2021

Suppose that $d_1 < d_2 < d_3 < d_4$ . We must have $d_1=1$ . If $d_1,d_2,d_3,d_4$ were all odd, $N = d_1^k + d_2^k + d_3^k + d_4^k$ would be even, which make $d_2=2$ , which is a contradiction. Thus at least one of $d_1,d_2,d_3,d_4$ is even, so $N$ is even, and hence $d_2=2$ . One of $d_3,d_4$ must be even, and the other must be odd.

If $d_3$ is even, we must have $d_3=4$ and $d_4=p>4$ an odd prime. But then $4q$ divides $N = 1 + 2^k + 4^k + p^k$ , and hence $p^k \equiv -1 \pmod{4}$ . Since $q=2^k+1$ is prime, $k$ is a power of $2$ , and hence is even. Since $n^2 \equiv 1 \pmod{4}$ for any odd number $n$ , it follows that $p^k \equiv 1 \pmod{4}$ . Hence this case is impossible.

Thus $d_3=p$ is odd, so we must have $p$ prime and $d_4=2p$ . But then $N = (1 + 2^k)(1+p^k) = q(1+p^k)$ is a multiple of $2p$ , and hence $p$ divides $(1+p^k)q$ . Thus $p$ divides $q$ , and hence $N=q^{k+1}+q$ , so that $N - q = q^{k+1}$ , and hence $q$ has index $\boxed{k+1}$ in $N-q$ .

On the power of divisors

2 solutions

0 pending reports