One single step, and U win..
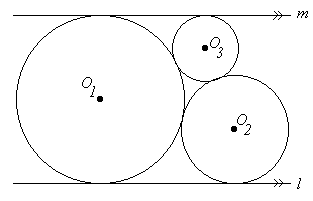 The circle centered
O
1
has radius
a
.
The circle centered
O
1
has radius
a
.
The circle centered
O
2
has radius
b
.
The circle centered
O
3
has radius
c
.
If
l
∥
m
and
a
>
b
>
c
, then find
b c a 2
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
What program did you make the diagram with
Log in to reply
I use Geogebra
Log in to reply
It looks like your links are down. Can you replace it with the formulas? Alternatively, use "Upload an image".
Not sure if this is a fair way of solving but here goes -
The configuration for a given pair of parallel lines (thus a given 'a') still has one degree of freedom. Thus the desired ratio must be invariant for all (b,c).
The relation should hold good even for a > b = c
Which gives a = 2b = 2c
Thus b c a 2 = 4
Is this approach rigorous? Any flaws?
Hi, Ujjwal. Your solution is fine as it is assumed without proof that b c a 2 is invariant. I suppose, though, that the more interesting question is to actually prove that this fraction is indeed invariant and equal to 4 , which Rudresh has done in his solution. The invariance is a surprising result, which is why I reshared the problem.
Log in to reply
Yes Brian, that is indeed a remarkable result. Wonder whether its discovery was accidental or there is something intuitive and physical/mechanical at its root. I solved it the same was as Rudresh, But not having much learning/skill in formal math, wanted to know in general if solving via a special case is acceptable, once the invariance is given.
By the way, talking of special cases, had an amaturish question: can the two lines be considered as arcs of infinite radii and obtain something more general for five circles?
Log in to reply
Yes, if the invariance is assumed then the question becomes that of finding what the invariant value is, in which case an examination of any "convenient" special case will do just fine.
I suspect that this invariance has some hidden significance, and your follow-up question may offer some clues. I'm thinking that Descartes' Theorem may be the best route to go here, but this will have to wait for tomorrow. :)
P.S.. I'm surprised when you say that you don't have much learning in "formal" math. Based on the excellent solutions of yours that I've seen, particularly in geometry, I had assumed that you were a teacher/professor.
Log in to reply
@Brian Charlesworth – You guessed right Brian! I do consider myself a teacher at heart and teach at the first opportunity. (Also do that via a YouTube channel). But that is mostly engineering/science and intuitive/visual bits of math/math solutions (to which geometry comes close). However that approach hardly works in algebra and even the geometry is often dismissed by the rigorous eyes as nothing more than 'hand waving' :-)
Lastly, thank you for mentioning Descarte's theorem! I just looked it up on Wikipedia and one figure there actually has a circle flattened to a straight line! This is one more addition to the gems i picked here. Others being Stewart's theorem and Pick's theorem and countless other fascinating results.
Log in to reply
@Ujjwal Rane – I value intuition over rigor, as it is a rarer ability. :) And thanks for mentioning Stewart's theorem; I often use Apollonius' theorem but now I see that it is just a special case of Stewart's theorem. Good to know.
Considering the centers of three circles as given, join the three centers to make a triangle named [O1 O2 O3].then draw the perpendicular projection of line O1 O3 on line 'm'.similarly draw projection of line O1 O2 on line 'l'.then apply the Pythagoras theorem.
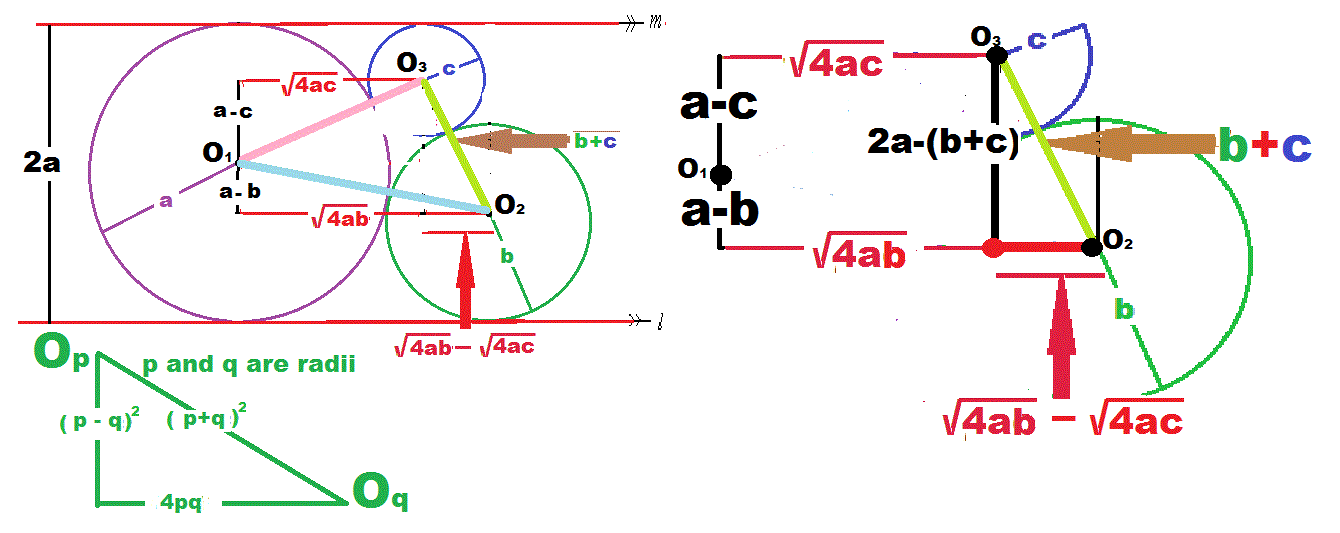
Noting how Pythagoras Theorem is applied to two tangential circles as shown in the green sketch, we get the red horizontal and black vertical components of O 3 O 2 = C + B and from the enlarged sketch applying Pythagoras Theorem we get { 2 a − ( b + c ) } 2 + { 4 a b − 4 a b } 2 = ( b + c ) 2 . S i m p l y f y i n g 4 a 2 = 2 b ∗ c ⟹ b c a 2 = 4
As I open discussion I saw Rudresh Tomar's same solution. Since his sketch is not very clear, I retained my solution.
∴ b c a 2 = 4