Only looks like the Archery aim!
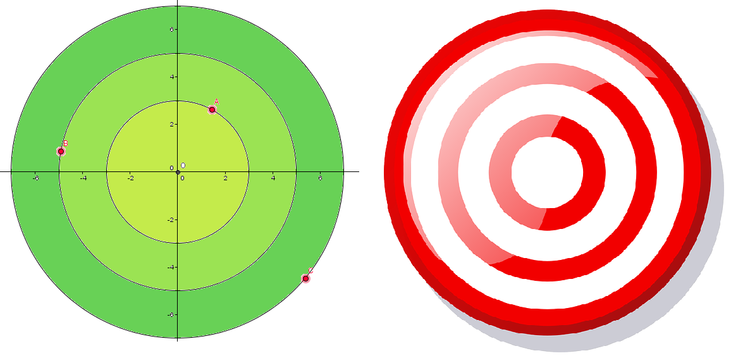 There are three concentric circles with center
O
and radii
3
,
5
,
7
units.
There are three concentric circles with center
O
and radii
3
,
5
,
7
units.
Points A , B , C are on these circles, one on each circle.
Find the smallest integer greater than maximum possible area of △ A B C .
Also see
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice Method ! Thanks , for Posting Solution . I'am not able to solve it.
Thank you very much Deepanshu bro! I was actually unable to find exact maximum area, but I made this question using GeoGebra. Actually the question came to my mind while solving problems of Complex Numbers, and yeah, your solution is same as the one using Complex Numbers...
Is it possible to use homothety?
Log in to reply
Sorry , I hear it first time , can you please explain what you mean ?
Log in to reply
Homothety is quite a useful tool, I've been using it in many olympiad problems, but I really don't see how homothety can give the area in this problem...
Very nyc solution to an excellent problem :)
How to solve the cubic equation after setting the derivative equal to zero?
 Imgur
Imgur
Suppose we have two of the points (B & C) of the optimum triangle. The third point A lies on a circle. If we were to move A keeping the area ABC constant, A must move along a line parallel to BC (Shown dotted). Moving to right of the dotted line gives more area, on the left we get less. Since area is maximized, the path of A must wholly lie on the left of the dotted line.
So the dotted line must be a tangent to the path of A - the circle, since the radius OA is perpendicular to it, it must be so to the base BC as well! Hence line AOm must be perpendicular to the base BC - an altitude.
For the same reason, Bn, Cp must also be altitudes that meet at O. Hence O is the Orthocenter of triangle ABC.
Taking OA as the x axis and Om = x; equate slope of CO to negative reciprocal of slope AB gives -
9 − x 2 2 5 − x 2 = − x ( 7 − x )
Solved this numerically to get x = 1.47 and the area 31.31
Could you check your equation? I think the correct RHS is − x ( 7 − x ) or x ( 7 + x )
Log in to reply
Thanks for letting me know @Cleres Cupertino ! I have corrected it now.
Very nice solution
As it is normal with you an elegant simple solution.
the question proposed is incomplete!! add the point that one can use a calc to find the roots of a cubic polynomial. well a pure geometric solution-> show that triangle ABC will be such that 0 (centre) is the orthocentre of ABC.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the “dot dot dot” menu in the lower right corner. This will notify the problem creator who can fix the issues.

Do you know how to prove that the center must be contained within the circle and be the orthocenter of ABC, in order for the area to be maximized? It's based on a very simple observation.
Log in to reply
So, what's that observation?
Log in to reply
See Ujjwal Rane's solution.
Log in to reply
@Anupam Nayak – Okay I'll do that, but that doesn't answer my question!
Log in to reply
@Saurabh Chaturvedi – He explains why with the observation.
After pages and pages of calculations, I found that if the radii have values r 1 , r 2 and r 3 , and if we name s = r 1 2 + r 2 2 + r 3 2 and p = r 1 r 2 r 3 , then the square of the circumradius x = R 2 is a solution of 1 6 x 3 − 8 s x 2 + s 2 x − p = 0 .
More over, as c i 2 + r i 2 = 4 R 2 for each side c i opposite of point lying on circle with radius r i and as area = 4 R c 1 c 2 c 3 , we have A = 1 2 3 ( 1 2 x − s ) 2 + 2 s 2 − 6 ( r 1 4 + r 2 4 + r 3 4 ) .
Good Problem!, the key is If we fix any one vertex keeping other two vertex as variable then maximum area won't affect . Since It is independent of reference frame. So Let us Fixed Vertex A ( 3 , 0 ) and also let parametric Points as B ( 5 cos α , 5 sin α ) & C ( 7 cos β , 7 sin β ) .
So area of Triangle ABC in determinant form is given by: Δ = 2 1 ∣ ∣ ∣ ∣ ∣ ∣ 5 cos α 7 cos β 3 5 sin α 7 sin β 0 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ Using Operation: C 1 → C 1 − 3 C 3 and then expanding about 3rd row we get :
Δ = 2 1 ∣ 3 5 cos α sin β − 3 5 sin α cos β − 2 1 sin β + 1 5 sin α ∣
Now Remind , Maximum value of a sin x + b cos x is nothing but a 2 + b 2 So let's rearrange above expression of area in this form:
Δ = 2 1 ∣ ( 3 5 cos α − 2 1 ) sin β − ( 3 5 sin α ) cos β + 1 5 sin α ∣ Δ m = 2 1 ∣ ∣ ∣ ∣ ( 3 5 cos α − 2 1 ) 2 + ( 3 5 sin α ) 2 + 1 5 sin α ∣ ∣ ∣ ∣ Δ m = 2 1 ∣ ∣ 7 3 4 − 3 0 cos α + 1 5 sin α ∣ ∣
Now simple differentiating it and equate to zero d α d ( Δ m ) = 0 , we find It's Maximum value as:
Δ m a x = 3 1 . 3 1 4 ⌈ Δ m a x ⌉ = 3 2