Only Two Lengths
This arrangement requires three different colors of string.
The diagram shows four black pins put on a board. Six colored strings connect each pair of pins, and the same-colored strings have the same length.
We would like to rearrange the four pins in such a way that we need exactly two different colors for the six connecting strings.
How many ways are there to rearrange the pins in this manner?
Note : The four pins must make a distinct shape for each solution. Rotations, reflections, and dilations are not considered new solutions.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I found these, but how do we know this is all of them?
Log in to reply
yes, how do we know this list is exhaustive?
find all the other shapes constructed with four pins (there are finitely many) and proof they have more than two distinct lengths. I didn't find all six shapes in this solution but I have managed to disprove some shapes. For example, a shape constructed with an equilateral triangle and an isosceles triangle that shares it's distinct side with the equilateral triangle.
I approached it from a counting perspective. Let m and n be the number of sides of each color/length, so m + n = 6. Assume m <= n. Consider each possible value for n:
-
n = 6: All four pins are equidistant, which is impossible in the plane (they would have to be the corners of a tetrahedron).
-
n = 5: The five equal edges must form two equilateral triangles with a common edge, which combined makes a rhombus with one diagonal the same length as the sides. The odd edge must be the other diagonal. This is solution 1.
*n = 4: The four equal sides must form either a quadrilateral (which by necessity is a rhombus) or an equilateral triangle with a "spur", another line segment of equal length extending from one of the vertices. In the first case, the two diagonals must be equal, forcing the rhombus to become a square, which is solution 2. In the case of the triangle and spur, let ABC be the triangle and AD be the spur. then BD = CD, so D must lie on the perpendicular bisector of BC. The only two possibilities where AD = AB = AC are solutions 4 and 6.
*n = 3: The three edges of one color must either form an equilateral triangle or a chain of 3 line segments joined end-to-end. In the first case, the fourth vertex is equidistant from the first three, i.e. it lies at the circumcenter of the triangle, which is solution 3. The second case is the most difficult to describe. Suppose the vertices are joined in the order ABCD by 3 blue edges, and the remaining 3 edges are red. Then ABC and BCD are each "blue-blue-red" isosceles triangles, meaning that angle ABC and angle BCD are congruent. If these angles are oriented in opposite directions (e.g. traveling from A to D involves one clockwise and one counter-clockwise turn), a parallelogram is formed with two red and two blue edges, which cannot meet the two-color condition (in fact, this is the situation in the counter-example from the puzzle description). In order to satisfy the two-color condition, then, both "bends" must be in the same direction, forming a trapezoid with three blue edges and one red edge. The only question that remains is, does such a trapezoid exist where the diagonals are also red? An appeal to intuition shows there is. Let b be the length of the blue sides, r the length of the red side, and d the length of the diagonals. We have 0 <= r <= 3b, and d is a continuous, increasing function of b. When b = 0, we have an equilateral triangle with "diagonals" overlapping the edges, so d = b. When r = 3b, the trapezoid degenerates into a straight line, and the "diagonals" have length 2b. Thus we go from r < d to r > d as b increases from 0 to 3b, so by the intermediate value theorem (applied to r - d) there must be a value of r where r = d. Furthermore, since d is an increasing function of r, this value must be unique, so solution 5 does exist, and it exists in only one form.
Excluding degenerate cases with edges of length 0, this exhausts all possible values of m and n, so these 6 solutions must, in fact, be all there are.
(EDIT: accidentally reversed the colors in the final paragraph, fixed now.)
Log in to reply
An easier way to describe your last trapezoid (solution 5) is: Take four vertices of a regular pentagon. The blue edges connect adjacent vertices, and the red ones connect the rest (vertices with another vertex "in-between" the ones connected).
Log in to reply
@Black Mephistopheles – Agreed, this is much simpler in terms of establishing existence. To establish uniqueness, unfortunately, it might still be necessary to use the argument above.
Take a look at my solution, I think my method can yield a proof.
I know even another way
then another variation of solution 4, another and another.......
Log in to reply
I don't see how you get variations of solution 4 while preserving a) one outlier edge has the same length as the three sides of the triangle, and b) the other two edges are the same length.
Where is 4th pin in 3rd solution?
Log in to reply
it is suppossed to be in the center, but following that logic we could attach an extra pin to the intersection between two lines of shapes 1,2,5 and 6 making them have 5 pins instead of 4.
Log in to reply
although I guess that would make the shapes have 8 line segments instead of 6.
The problem statement doesnt seem to exclude strings of zero length, so wouldn't any straight line with two pins at each end count as a valid solution?
Log in to reply
That wouldn't require two colors.
Log in to reply
But then wouldn't you be able to just make something like an isosceles triangle with one vertex having 2 pins on it, thus only requiring two colors?
I just guessed.
I put six. Did not work
Why 3 and 4 are not the dilations that are not considered new solutions?
Solution 3 only has 3 pins
very funny!! thank you.
Could you explain no 5?
Four pins form
(
3
4
)
=
4
triangles (assuming that no triple of pins is collinear). Since we are constrained to exactly two different lengths, each triangle will be at least isosceles, which means that at least two its sides will be equal. Consider isosceles triangle with base
A
B
and base angle
α
. Vertex at the top is defined by the intersection of the triangle legs and denote it with
C
. Next, construct two circles with each vertex as a center with radii
A
B
and
A
C
, respectively. When three of these circles meet, we get a set of 4 pins which satisfy our conditions. Check out the animation:
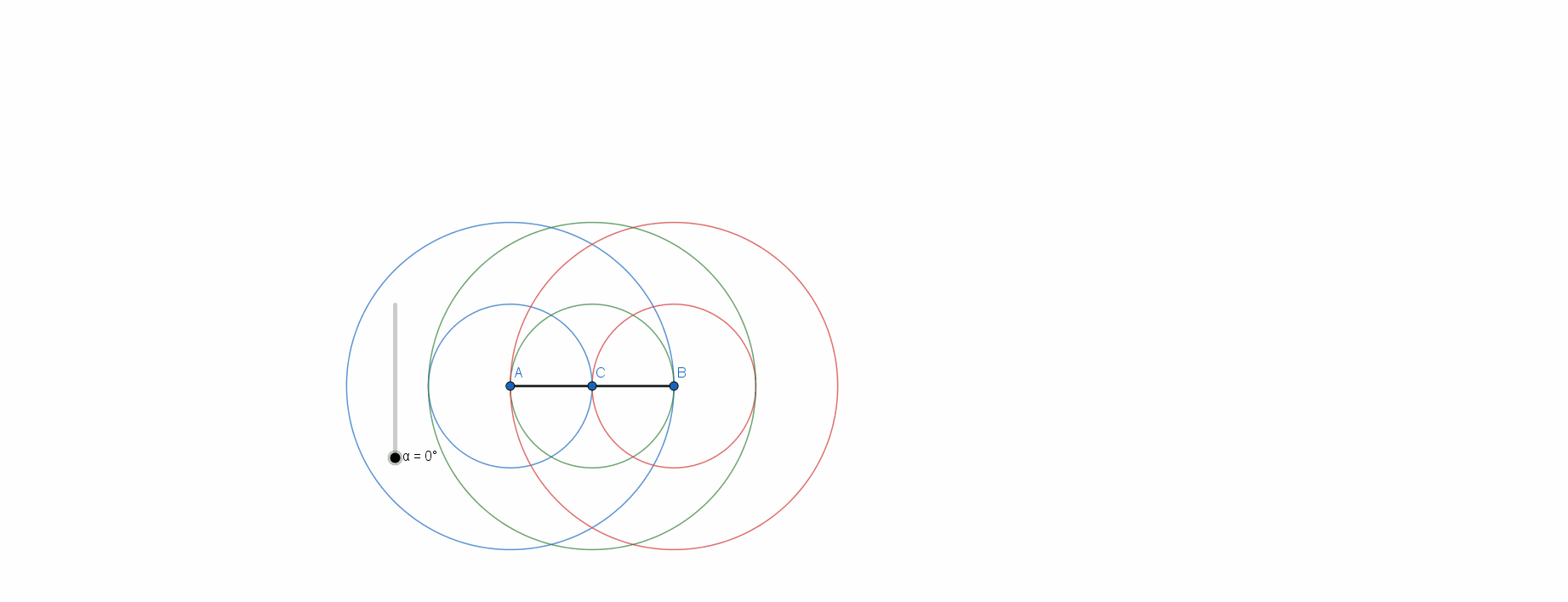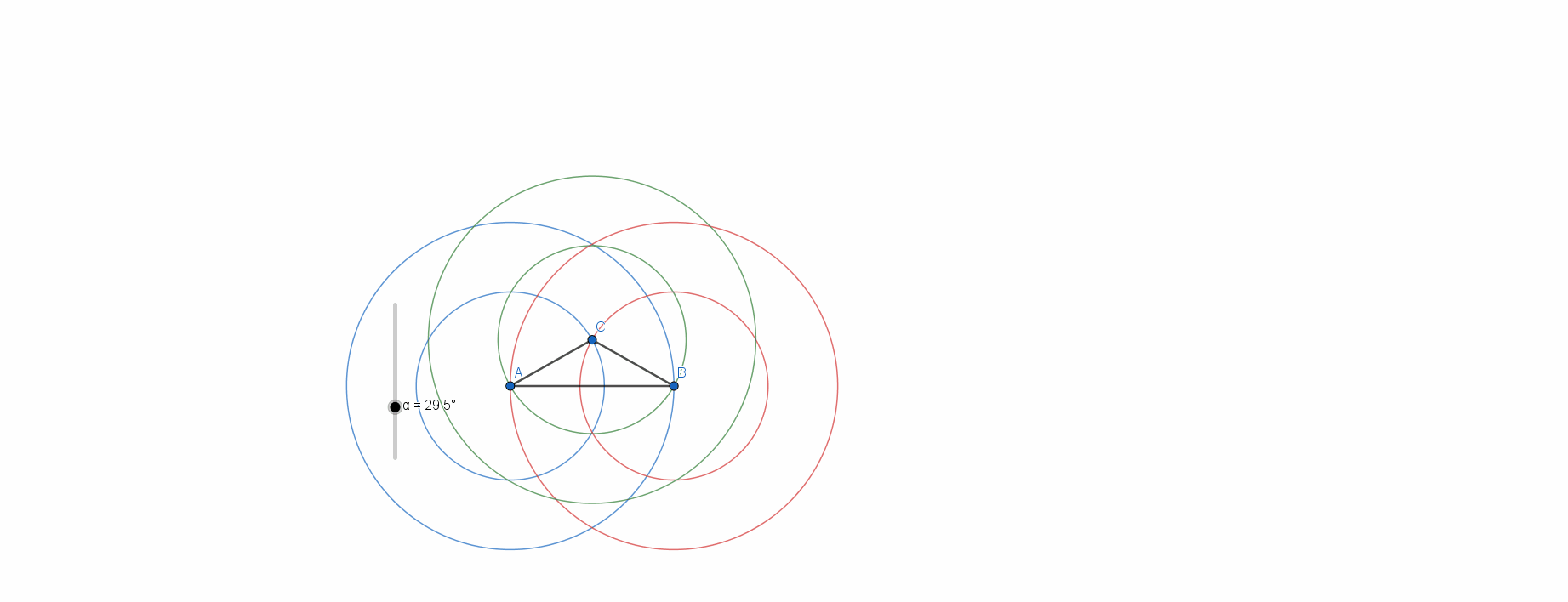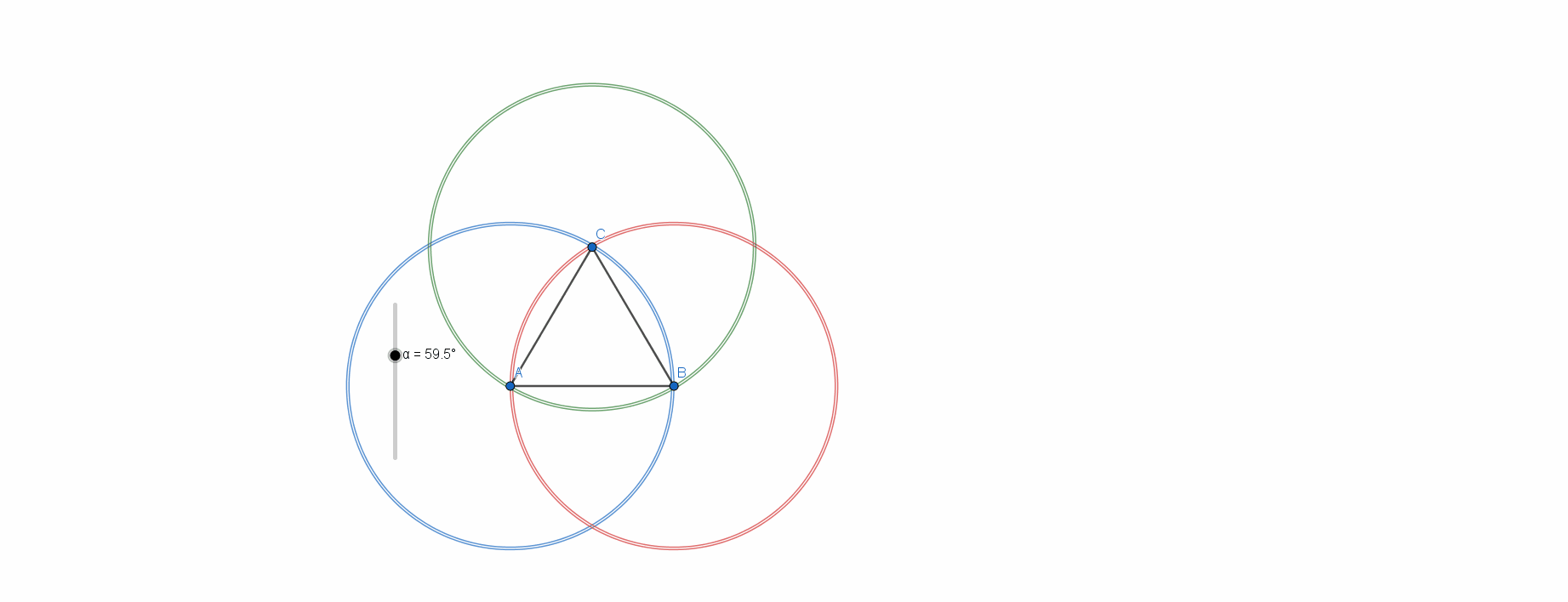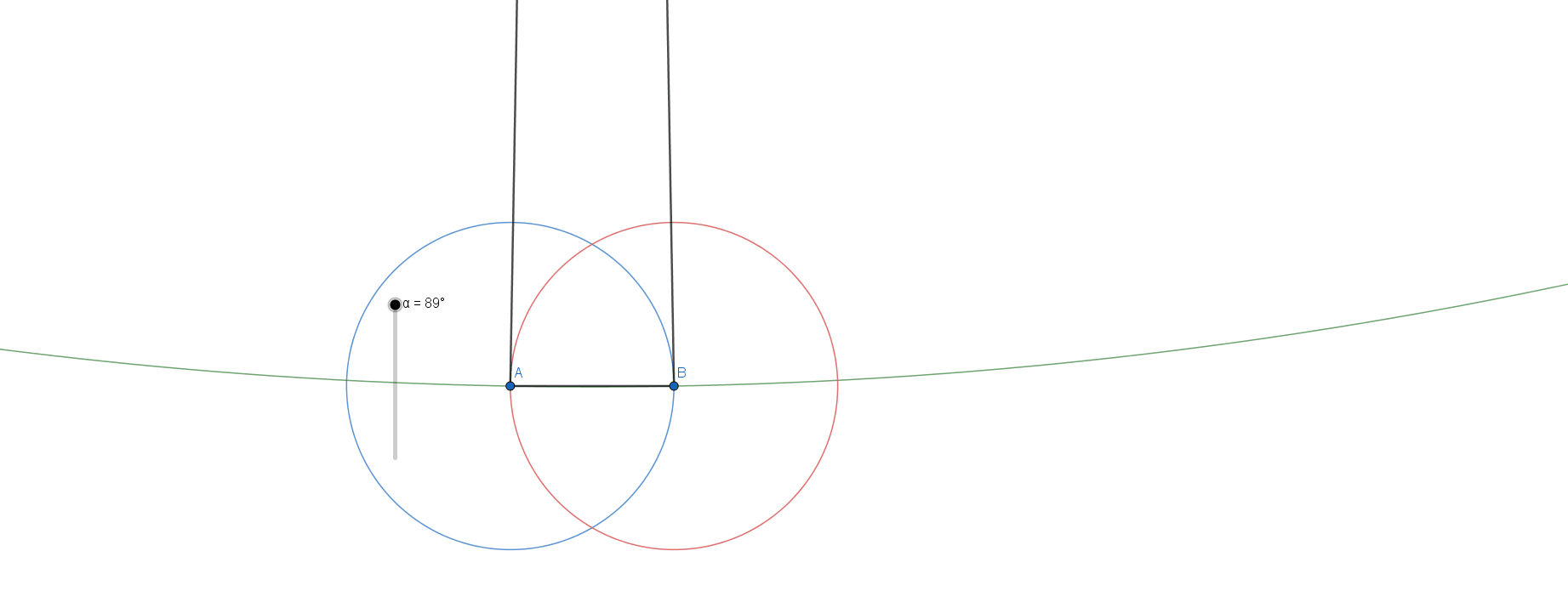
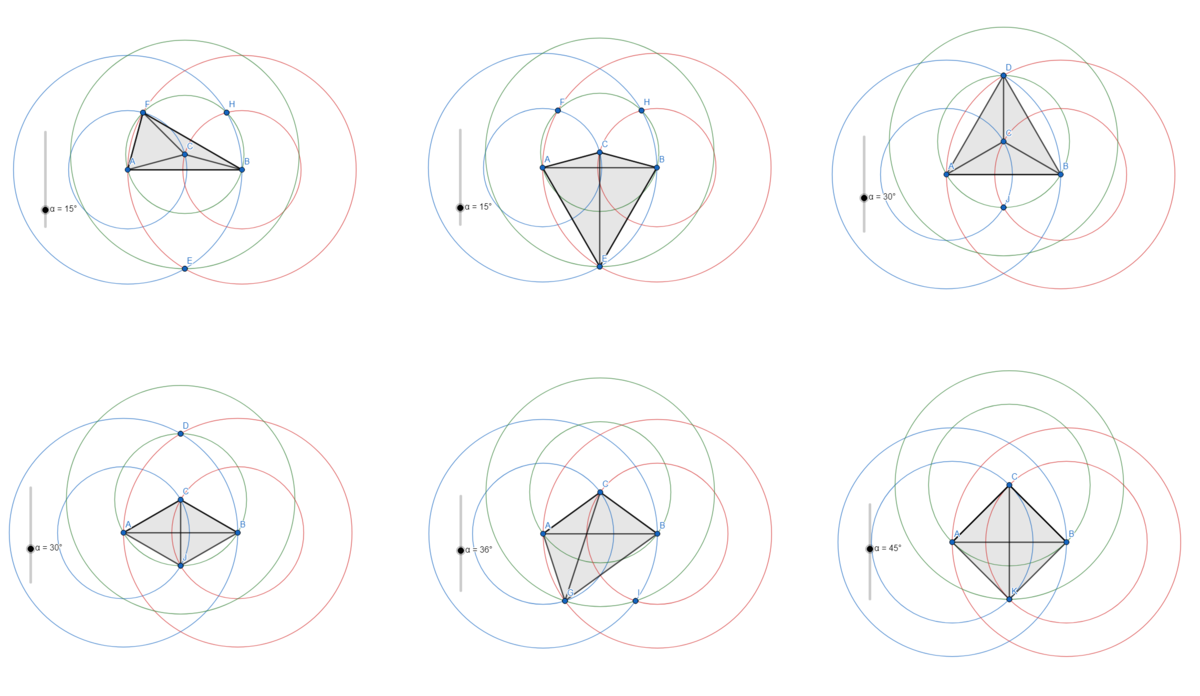
If we set up the equations of each of these circles, we can algebraically prove that the above configurations are the only possible solutions.
Solution seems to miss the degenerate cases where pins overlap, which gives us 1 more solution with 1 off-colour string (equilateral triangle with a doubled point), 1 more with 2 off-colour strings (line segment with both ends doubled), and 1 more with 3 off-colour strings (line segment with one end tripled), with the off-colour strings for each of those having length 0, for a total of 9 solutions. Please fix either the problem description or the answer.
Two pins together requires no string.
Log in to reply
But per the problem description, we still attach a piece of string between them, with length 0. In the real world, that would be the same as no string, but whether you allow 0-length strings in mathematical problems is a choice. If it's not specified, the convention is that they are allowed. This isn't just a whim either: many mathematical theorems become a lot more complicated to express if 0 isn't considered a valid distance between two points.
In this case, I suspect there to be a pattern in the amounts of possible string lengths if we start looking at n points separated by k discrete distances for arbitrary natural n , k , and that pattern will likely have a simpler formula when counting 0-length strings than when excluding them.
improve more
That was my concern as well. I would argue though, that a total of 8 is achievable, since it is specified that the shapes should be unique, so the line segment with both ends doubled and the segment with one end tripled are just one and the same (shape-wise).
Clockwise from top left:
※ Little mistake in the drawing: the last pin should be at the triangle's center for solution 3!