Opening a parachute
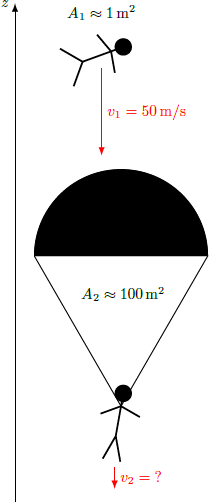
Without opening his parachute, a skydiver reaches a fall velocity of v 1 = 5 0 m/s . When he does open the parachute, he's braked by additional air resistance. After a while, he finally arrives at the ground.
At what fall velocity v 2 does he reach the ground?
Details and Assumptions:
- The air frictional force F f = F f ( ρ , A , v ) depends only on the density of the air ρ , the cross-sectional area of the skydiver A , and the velocity v . Neglect the effect that the shape of the falling object has on the air frictional force.
- The cross-sectional area without the parachute is A 1 ≈ 1 m 2 and that with the parachute is A 2 ≈ 1 0 0 m 2 .
- The density of the air is constant.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Markus, what orientation is the person free falling for the drag coefficient you quoted. Orientation does effect projected area but feet first should be different than spread eagle or tumbling. I recall Fluid Dynamic Drag by Hoerner had a lot of data including the drag of a pilot and seat when ejecting from a plane.
Log in to reply
That's a very good question. I found these numerical values for the resistance coefficient on the german Wikipedia page and they may not be absolutely reliable. From its numerical values, the coefficient of resistance of man corresponds to that of a full hemisphere (~ 0.8) and the parachute is practically a hollow hemisphere (~ 1.3 - 1.4). It was stated that man stood by the experiment. However, one can also find completely different numerical values. For example, Usain Bolt has a drag coefficient of 1.2 in the sprint.
I can not help you with too much practical background knowledge on aerodynamics. Years ago I attended a single aerodynamics lecture and read a single textbook, that was very theoretical.
The formula you explained by dimentional analysis can be explained in a non very rigorous way like this: You push air molecules below you at your own velocity v, they then return their own mentum by Newton (II) to you so that the force F you recive is F=dp/dt=dmv/dt (the velocity of all the air moleculas is constant)=vdm/dt=vdAρh/dt=vAρdh/dt=v^2Aρ. But in fact the shape of the object also matters so we introduce a constant c having as you said F=cρAv^2. I hope this can help, in fact you can see better explanation on the classical mechanics, momentum, Brilliant Premium quiz.
Log in to reply
You are absolutely right. The air resistance can be explained by the fact that there are particles in the air, which bounce off the moving object. If the object moves faster, more often collisions occur and each collision is more intense. The number of collisions is also proportional to the air density and the cross-sectional area of the object. That's basically the whole physics behind it.
This physics is also called kinetic gas theory. Originally, I wanted to post a problem where air friction force should be derived explicitly from this kinetic gas theory alone. But since my thermodynamics problem were not so popular, I rejected this idea.
Why does the value for gravitational force in your equation negative?
Log in to reply
The forces point in opposite directions. The gravity is directed to the ground (negative direction) and the air resistance points upwards (positive direction).
Yeah. Dimensional analysis is the way to go on this one.
Yes we should apply dimensional analysis when we don't know formula
For air, where the viscosity is relatively low, the drag force varies as F = c A v 2 , where c depends on the shape of the object, A is the cross section facing the air stream, and v is the velocity. Without the parachute the steady state (limiting) velocity obeys F 1 = m g = c 1 A 1 v 1 2 . With the parachute we have F 2 = m g = c 2 A 2 v 2 2 . For the estimation we assume c 1 = c 2 . Dividing the two equations yields
1 = A 2 v 2 2 A 1 v 1 2
or
v 2 = v 1 A 2 A 1 = 5 0 1 0 0 1 = 5 m / s
Why they did not give explicitly the formula for the drag force? What a shame. Good job, Laszlo.
Log in to reply
This kind of drag force is used to explain why keeping the speed limit helps in fuel consumption. Double the speed -> quadruple the losses.
Log in to reply
keeping the speed limit helps in fuel consumption' how? can you explain please
Log in to reply
@Ridoy K – A significant part of the engine's power is used to overcome air resistance. As the drag force increases with the square of the velocity, we can save fuel by keeping the velocity down. For example, in the USA in many places the speed limit is 55 miles per hour (about 90 km/h). If someone drives at 80 miles per hour (that is about 130km/h, the speed limit in Italy), the drag force will be about ( 8 0 / 5 5 ) 2 ≈ 2 times larger and the fuel consumption will also increase by approximately the same factor.
If, on the other hand, the drag force would be proportional to the speed (Stokes's law), the increase of the force would be only by a factor of 8 0 / 5 5 ≈ 1 . 5 . The rolling drag force at the wheels and the sliding friction at the axles is approximately independent of the velocity. If that dominates the energy losses (e.g. driving in perfect vacuum) the fuel consumption would be independent of velocity.
The formula is not given explicitly because you are expected to do a dimensional analysis yourself, given the information that F only relies on ρ, A and v, which is actually the main task of this problem. The rest is simple.
Log in to reply
Well there can be constant which has dimensions itself, just like in the stoke's law
Log in to reply
@Pranav Rao – Indeed! You are right. For this problem, an additional assumption is needed to exclude this situation. In the problem description it is stated:
…the air frictional force F depends only on the density of the air ρ, the cross-sectional area of the skydiver A, and the velocity v…
or, as a formula, F = F(ρ, A, v).
Maybe it means that, if there were any dimensional constants, then they would count as relevent factors and appear in the formula. So here is none. Anyway the problem is not given clearly enough.
I will consider your remark next time. I did not know that so the drag force as a function did not open any proper ideas ahead. I do not see that dimensional analysis is appropriate. Because you can still have something like F = const * A^3 * ρ * v^(3/2) and say that const has an appropriate dimension. At the end of the day, googling the formula is a trick of the task, isn't it? Never mind, never mind. I am upset.
Log in to reply
@Nazariy Boychuk – Convincing…I now agree that googling is the better way.
Isn't it F=cρAv^2? You missed the drpendence on the air density, (although it is here always the same).
Log in to reply
the density can be incorporated to the constant c.
Log in to reply
I thought that but then you say "c depends on the shape of the object" true but you could also add "and is proportional to the air density" or something.
Log in to reply
@Pau Cantos – As you said the density is the same for the two situations in this problem. It becomes important only if you want to derive the equation by dimensional analysis, as in Markus Michelmann's solution. .
I can't understand why you work in steady state isn't v= 0 in the steady ?
Log in to reply
It is a question of convention. Generally, "steady state" is used when the important parameters of the problem are independent of time. Here v=const is "steady" in that sense.
When v=0, the system is "at rest".
Yeah Walter Lewin must have taught you this
Log in to reply
No, it was actually Miklos Vermes, back in Hungary many years ago.
from where did you get this formula (F=cAv2)?
Log in to reply
One can Google "air drag" or "air friction". One can go to Wikipedia, and search for the same. Or derive the equation with dimensional analysis, as Marcus did in his solution.
U can also find this relation by dimensional analysis, F =cAv²
The equation for the air resistance acting on an object is given by 2 p C A v 2 , where p is the air density, C is the drag coefficient and v is the velocity. It says in the assumptions to ignore the effect shape has on air resistantance, and since this is basically what the drag coefficient is, we leave it out of the formula. At first we substitute our given values for the skydiver with out a parachute:
F a i r = 2 p × 1 × 5 0 2 = 1 2 5 0 p
We are not given the air density, but this is ok. We then substitute the values for the skydiver with his parachute in use:
F a i r = 2 p × 1 0 0 × v 2 = 5 0 p v 2
Now because the total air resistance, in a way, does not change (instead others parameters do, like surface area), we can set these two answers equal to each other:
1250p = 5 0 p v 2 , which yields v = 5.
You did the same thing as done by Laszlo
I just multiplied velocity proposed by 3.6 tout obtain the corresponding velocity in km/h. The results were aller strange: 5km/h is too slow and 57 is too fast so 18 km/h seemed the only remaining possibility (it corresponds to 5 m/s)
When initial speed of fall was 180 km/h, then even 57 km/h can not be ruled out just intuitively.
To establish an equation for the frictional force, we use the dimensional analysis. The relevant quantities each have the units [ F ] [ ρ ] [ A ] [ v ] = N = kg ⋅ m ⋅ s − 2 = kg ⋅ m − 3 = m 2 = m ⋅ s − 1 Now we try to create a force from the quantities ρ , A and v : ⇒ ⇒ ⇒ [ F ] kg ⋅ m ⋅ s − 2 ( α , β , γ ) F f = ! [ ρ ] α ⋅ [ A ] β ⋅ [ v ] γ = kg α ⋅ m − 3 α + 2 β + γ ⋅ s − γ = ( 1 , 1 , 2 ) = c ⋅ ρ ⋅ A ⋅ v 2 , [ c ] = 1 The constant c is dimensionless. This is the only possible form that the friction force equation can have, because only in this way can we get a quantity with a unit of force. However, this does not apply if the viscosity of the air also plays a role, because then an additional parameter has to be considered, especially in the limit of high viscosity, so that in this case applies F f ∝ v .
After a long fall the parachutist reaches a final velocity v ∞ = lim t → ∞ v ( t ) , so that the sum of gravitational force and friction force is zero: ⇒ ⇒ F g + F f − m g + c ρ A v ∞ 2 v ∞ = ! 0 = 0 = c ρ A m g ∝ A 1 When opening the parachute, only the cross-sectional area A changes, so that will be able to write ⇒ v 1 A 1 v 2 = v 2 A 2 = A 2 A 1 v 1 ≈ 1 0 0 1 ⋅ 5 0 s m = 5 s m In fact, the frictional force depends on the shape of the object. The equation for the drag is according to the textbook: F f = 2 1 c w ρ A v 2 with the dimensionless parameter c w , which is for a parachute c w 2 ≈ 1 . 3 3 and for a human c w 1 ≈ 0 . 7 8 . Taking the c w -value into consideration, we therefore obtain the final velocity v 2 = c w 2 A 2 c w 1 A 1 v 1 ≈ 3 . 8 s m which is a bit smaller as our previous value.