Optical illusion

Draw one more diagonal that connects the two remaining endpoints (the one on the left side of the cube). We now have a triangle. All of its sides are equal in length (all of them are face diagonals of a cube), so it's an equilateral triangle and the angle formed between any pair of the lines is $\boxed{60^\circ}$ .

The red lines can make, with another line, an equilateral triangle, because they are diagonals, so, this angle is: $\boxed{60^{o}}$

Well, I thought it was 90, 90 was the bottom answer in the email I got about this problem, logged in, clicked the bottom answer on the site, after which I saw it was actually 60 that I clicked on, how's that for a Zen calculation!

Equilateral triangle formed

Turn it around in your head and think: it is cutting from vertex to vertex to vertex, so all three sides of the resulting triangle are equal, hence forming an equilateral triangle. equilateral triangle: 180/3=60 and theres your answer!

Let the origin of a coordinate system be at the intersection of the two red lines. Let the "x" direction be to the right, the "y" direction be into the diagram, and the "z" direction be up. Let's also assume for convenience (without loss of generality) that the cube has side lengths of 1.

One of the red lines can be described as the vector $\vec{a} = (-1, 0, -1)$ . The other can be described as the vector $\vec{b} = (-1, 1, 0)$ .

$\vec{a} \cdot \vec{b} = (-1)(-1) + (0)(1) + (-1)(0) = |\vec{a}||\vec{b}|\cos(\theta)$

$1 = \sqrt{2} \cdot \sqrt{2} cos(\theta)$

$1 = 2 cos(\theta)$

$\theta = 60°$

if we consider triangular prism based on red lines connecting triangular surface, then it's very easy to understand that base is equilateral triangle. And hence answer is 60 degree....:)

If you connect the two points by drawing a line between them, you can see you have just made an equilateral triangle, where each side is simple a diagonal of one side of the cube. (Since it is a cube, all of these lengths are equal). Equilateral triangles are also equangular, so 180/3=60 degrees.

If you draw the other diagonal of the triangle, passing through the two points, you will realise that the triangle so formed has all its sides equal, and hence it is an equilateral triangle. Thus the angle is 60º

Prior knowledge. The cube is the complimentary solid (platonic) to the octahedron - eight equilateral triangles. The eight faces of the octahedron correspond to the eight vertices of the cube, so 60°.

Imagine tilting the cube such that both the diagonals are on xy plane. Now the diagonal at the third face ie the non connecting end points will form an equilateral triangle, and all angles in equilateral triangle are 60

The two lines given are diagonals of a cube. They have the same length. If you connect their end points together, that's another diagonal. You have an equilateral triangle and therefore the angle between the two initially given lines is a 60 degree angle.

It is simple.. as you can see the two diagonals, can be proven as equal to each other due to the fact that they are diagonals of the intersecting faces of the cube... and if you draw a line from the endpoints of the two diagonals, you will form another diagonal of a face... considering that the three faces are congruent to each other, the diagonals have the same measurements that makes the formed triangle an EQUILATERAL AND AN EQUIANGULAR TRIANGLE where all angles are equal to 60°...

Red lines are drawn diagonally across 2 of the faces. Because the object is a cube, if a 3rd line was drawn on the left face, an equilateral triangle would have been created. Therefore, the angle shown is one of an equilateral triangle, hence 60 degrees

A cube has congruent diagonals, and both diagonals form two sides of a triangle, with the remaining side as another diagonal of the square. You find yourself with an equilateral triangle, thus arriving at the conclusion that the angle formed by the two diagonals/sides is 60 degrees.

Forget all the math work. Imagine drawing a third diagonal to complete a triangle between the ends of the two red diagonals. Since the cube is ...well... A cube, all the diagonal lengths would be the same, thus we would have an equilateral triangle. And every angle in an equilateral triangle is 60 degress. 👍👍👍

If you draw another line to complete the triangle, you will see that all 3 angles are the same. They are all diagonals at the vertices. Therefore, 180/3 =60

The solution is simple, all the faces of a cube are the same, so the diagonals are all the same. If you imagine the third side of the triangle and realize it's the same length as the other two sides then it must be an equilateral triangle meaning every angle is 60.

Damn easy question you just need to imagine an eqillateral triangle made by the face diagonals

I saw a triangle drawn by the diagonals, then, knowing that every triangle has 180 degrees, and that every diagonal is a cube measures the same, is an equilateral triangle, so, every single angle is the same, 180/3=60

Clearly every side of the triangle will have same length i.e. 1.414 times the side of square. Thus, this is an equilateral triangle which has angle of 60 degree.

Diagonals of every face of a cube are of same length, here we have two sides and so with the third diagonal, triangle is complete! So angle is 60 degree

it is clearly an equilateral triagle

1ºWe can make a triangle with that 2 red lines 2ºwe can conclude that all the lines have the same length, because all of them are diagonals of the squares. 3ºso 3 angles of the triangle are equal, so:

180=3x

x=60

answer: all the angles of the triangle have 60 degrees, including the one from the question.

for me this is the easiest way to resolve this problem what do you think? hope this was helpful

There is no need of computation or any calculation here. If the other diagonal is connected, it forms an equilateral triangle and we know that an equilateral has an angle of $60^\circ$ on each vertex.

It's a cube so the diagonals are congruent, so all three sides are congruent, thus it's a equilateral and equiangular triangle and the angles are 60 degrees

Let's go with some vector calculation: When you flip the screen upside down, then you can imagine the corner where both edges come together as the origin of a coordinate system. Then edge1 can be described as $e_1 = (1|1|0)^{T}$ and edge2 as $e_2 = (0|1|1)^{T}$ (T means transformed, so we can write those vectors in one line). For the angle $\theta$ it is: $\cos \theta = \frac{|e_1 \cdot e_2|}{|e_1|*|e_2|}$ which leads us to $\cos \theta = \frac{|1*0+1*1+0*1|}{\sqrt{1^2+1^2+0^2}*\sqrt{0^2+1^2+1^2}}$ , which is $\cos \theta = \frac{1}{2}$ , which leads us to $\theta = 60^\circ$

I do not rely on intuition, so I computed :p.

$(-1,0,1).(-1,-1,0) = 1 = \sqrt{2}\times\sqrt{2}\times cos(\theta)$

So $cos(\theta)=\frac{1}{2}$ which means that $\theta=60°$ :)

The easiest solution is to draw an imaginary line between the 2 unconnected points, creating an equilateral triangle. If you don't understand this, I invite you to think in depth about the spatial relations involved. It's best to use a visual aid, such as a physical cube and diagrams of your own making. From there, it's easy from many directions to prove that each angle in an equilateral triangle is 60 degrees. That is the geometric method I used to get the answer.

The more robust and general method is rooted in vector algebra. This is somewhat loftier, but should be comprehensible in the context of a complete high school education.

There are several way to go about it, but the simplest is to look at it as a 3 dimension system in Cartesian coordinates, taking the top, closest, right-hand corner (the vertex of the angles) as the origin. Consider the cube to be a translated unit cube (each side length=1).

Therefore the top line can be represented as the vector <-1,1,0> and the bottom line as <-1,0,-1>. Use vector identities concerned with the angle between two vectors to find the angle between these.

I used the fact that the dot product of two vectors equals the product of both magnitudes and the cosine of the angle. This is well described in this link: example link with good formatting/pictures/examples. Simple algebraic rearrangement of the equation gives: arccos( dotproduct / productofmagnitudes ) = angle. Again, visit the link for a visual and formatted equations.

Don't know if anyone posted this method, but if a line is imagined on the left side connecting the ends of the red lines, those three form a plane which is an equilateral triangle. Each angle is 60 degrees. Most basic way I could see. Though probably by the most robust.

All the sides of cube are same so all angles of triangle will same .. means equilateral triangle. So the andle will be 180/3=60.

Purely geometric solution: Let's call the angle ABC so we know what we're talking about. B is the vertex and A and B are the end points of the two line segments forming the angle.

Line segments (LS) AB and BC lie on the diagonals of two squares that are the faces of a cube (Given)

LS AC, which completes triangle ABC, lies on the diagonal of a third face of the cube (also given in the diagram)

All sides of a cube are the same length (property of cubes), let's call this X.

LS AB=√(2X^2) (Pythagorean Theorem) LS BC=√(2X^2) (Pythagorean Theorem) LS AC=√(2X^2) (Pythagorean Theorem)

Therefore, LS AB=LS BC=LS AC

Since all three sides are congruent, triangle ABC is an equilateral triangle (definition of equilateral triangles)

All three interior angles of Triangle ABC=60° (property of equilateral triangles) (in euclidian geometry)

Therefore, angle ABC=60°

the two diagonals are in different plane surface. so, we have to think of another surface in which these two diagonal lie.

'm pretty bad with latex, so I did my on word documents, using the Cambria Math font.

We shall define the bottom left corner towards us (which I shall call A) as (0,0,0) in the spatial coordinate system of (x,y,z) (x is left to right, y from us away and z from bottom to top). Thus top right corner on our side (which I shall call B) is (1,0,1) and the top left corner away from us (which I shall call C) is (0,1,1).

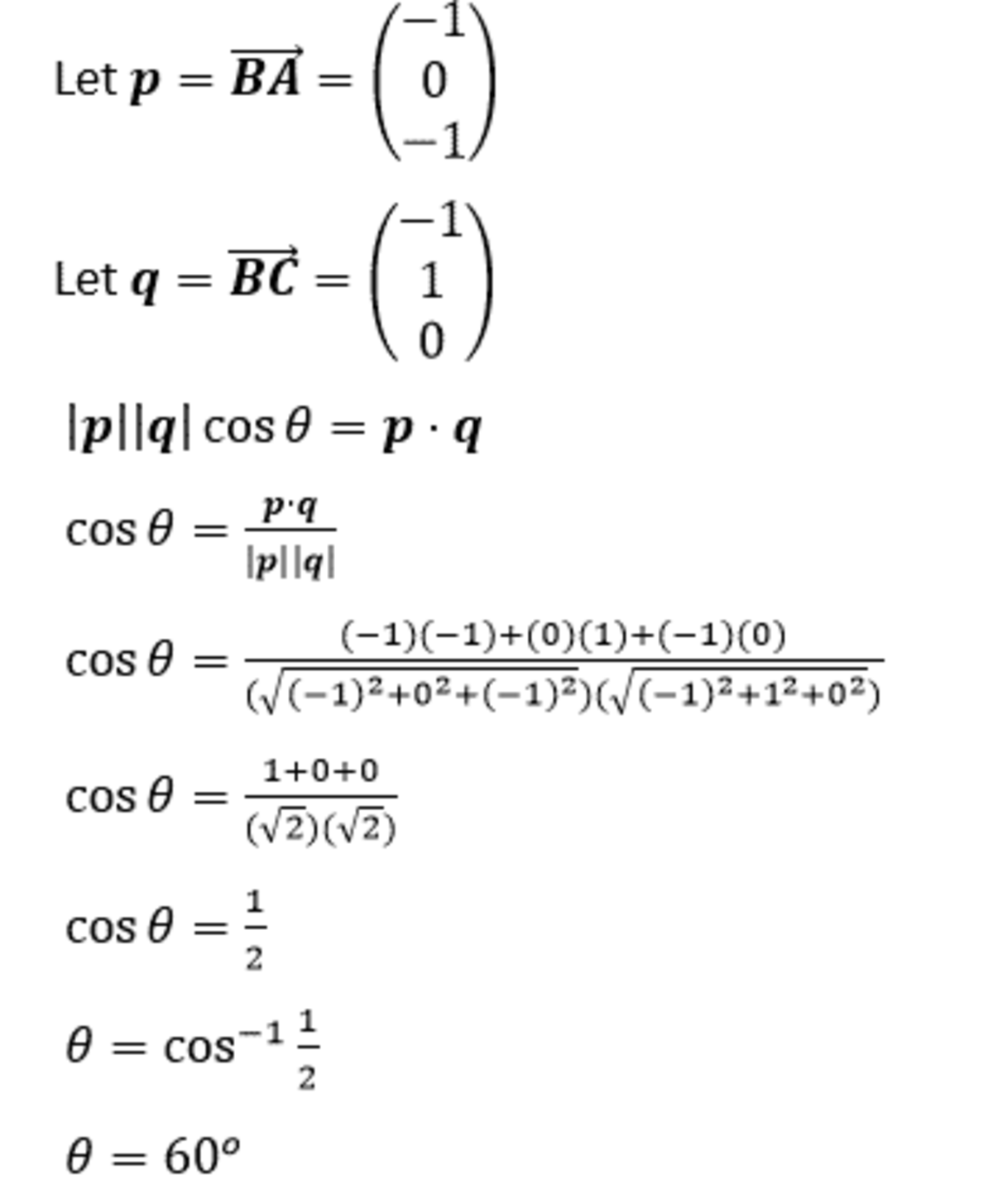
In the cube all the triangle dimensions are same...so all the angles in triangle are same...so angle is 180/3=60°

Since the three sides of the triangle are the diagonals of squares of same dimension, which makes it an equilateral triangle. Angles of an equilateral triangle are 60..

cube = 3d so 60

I used a vector method which has given me the right answer, but I'm not sure how valid my solution is, haha.

Let the cube have side length a, and let the vertex of the cube where the two red lines meet be the origin.

Let the x-axis be the right hand edge of the front face. Let the y-axis be the top edge of the front face Let the z-axis be the right hand edge of the top face.

Let's model the two red lines as vectors pointing away from the origin.

In that case, the red line on the front face can be described by the vector (a, a, 0). The red line on the top face can be described by the vector (0, a, a)

To find the angle between the two vectors, we use the scalar product.

formula: u. v = |u||v| cos X

The length of each vector is sqrt(2a^2)

Taking the dot product of the vectors in component form, we have the dot product = a^2

Hence, we have a^2 = sqrt(2a^2) * sqrt(2a^2) cos X

a^2 = (a*sqrt(2))^2 cos X

a^2 = 2*a^2 cos X

1/2 = cos X

X = 60 degrees.

To all the people who are still confused on this, draw an imaginary third line to complete a triangle. Since it's a cube, that triangle is equilateral. Since all sides are the same length, all angles are the same as well. 180/3=60

As there is a cube, when all the diagonals are joined it forms an equilateral tringle... sum of all the angles in trigle is equal to 180 degree. so the ans is 60 degree

This is the maths one needs to solve it via vectors.

A(vector) = (0,0,0) --> (1,1,0) = (1,1,0) B(vector)= (1,1,0) --> (0,1,1) = (1,0,-1)

A•B= 1 + 0 + 0 = 1

|A| = √2

|B| = √2

cosθ = (A•B) / (|A| x |B|) = 1/2

arccos(1/2) = 60°

a.b=|a||b|cosx

Assuming each side of the cube was 2 units long...

4=8cosx Cosx=0.5

There for x (the angle) is 60°

Think of it as simply forming an equilateral triangle, which has an internal angle of 90 degrees. Simple 😄

For those struggling to see why the answer is 60 degrees, remember than we need a plane or 2D triangle to define the angle. The only way we can find such a triangle that contains the required angle is by joining the two ends of the red diagonals already drawn on the diagram. This creates a triangle (in 2D) that has three equal sides (diagonals of the cube's faces). Each angle in an equilateral triangle is 60 degrees. Abhay's diagram shows this.

Right on the first try. Could tell just looking at the picture that it was 60°. Only 18% get it right though? o.O

find vectorial form of three orthogonal sides and find out the vectorial form of the mentioned diagonals.

Then take dot product which turns out to be 1/2.

So, cos inverse 0.5 is 60 degrees.

Yep you can draw in another diagonal on the left face of the square, and it makes an equilateral triangle (since all sides of a cube are equivalent, each of the diagonals are also equal) that lies on the plane that intersects the square diagonally, in which all three angle measures are 60! (Pretty much what Abhay said. )

60 degress Equilateral triangle as all the sides are same

It forms an equilateral triangle. Thus, the angle is 60°

To make it easier to solve,join the two red lines by another,it forms an equilateral triangle,hence equiangular triangle. Since all the angles in equiangular triangle are 60 degrees ,required angle is also 60 degrees