Orange Shaded Area

Let $O$ be the center of the circle and line $AC$ cuts the circle at $D$ . Since $\triangle ADO$ is an isosceles triangle, $\angle ADO = \angle DAO = \theta$ . Then $\angle DOB = 2 \theta$ . The area of the orange region is given by:

$\begin{aligned} A_{\color{#EC7300}\text{orange}} & = \text{Area of sector }DOB + \text{Area of }\triangle ADO \\ & = \theta r^2 + \frac 12 r^2 \sin \angle AOD \\ & = \theta r^2 + \frac 12 r^2 \color{#3D99F6} \sin (\pi - 2 \theta) \\ & = \theta r^2 + \frac 12 r^2 \color{#3D99F6} \sin (2\theta) \\ & = \boxed{\dfrac 12 \big(2\theta + \sin (2\theta)\big) r^2} \end{aligned}$

A "Beating the Test" solution:
For $\theta \rightarrow \frac{\pi}{2}$ , half of the circle will be filled and $A \rightarrow \frac{\pi r^2}{2}$ . Plug $\theta = \frac{\pi}{2}$ for each of the choices:

$\frac{\pi r^2}{2}$

$(\frac{\pi}{2}+1)r^2$

$2(\frac{\pi}{2}+1)r^2$

$\frac{\pi r^2}{8}$

So the first choice must be correct.

The question is the same as asking, "What is the area delimited by the polar curve $r = 2a cos\theta$ , the half line $\theta = t$ and the pole?"

To prevent confusion, I replaced $r$ in the diagram with $a$ , and $\theta$ in the diagram with $t$ , so that I can use the $r$ and $\theta$ as variables in the conventional polar way.

$r=2a cos\theta$ , by the way, will appear like this on a polar graph:

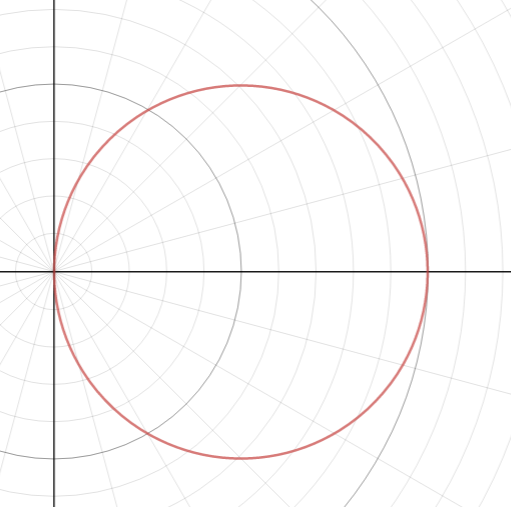
To calculate the area, I will use the formula: $Area = \int_{a}^{b} \frac{1}{2} r^2 d\theta$ ,

And $\frac{1}{2}r^2 = (2acos\theta)^2 = \frac{1}{2}4a^2 cos^2 \theta = 2a^2(\frac{1+cos(2\theta)}{2}) = a^2(1+cos(2\theta))$

Therefore the area is: $Area = a^2 \int_{0}^{t} 1+cos(2\theta) d\theta = a^2[\theta + \frac{sin(2\theta)}{2}]_{0}^{t} = \frac{1}{2}(a^2)(2t + sin(2t))$ ,

Since t and a are just dummy variables, using the given variables in the problem: $\frac{1}{2}(2\theta + sin(2\theta))r^2$

I will use the following diagram: 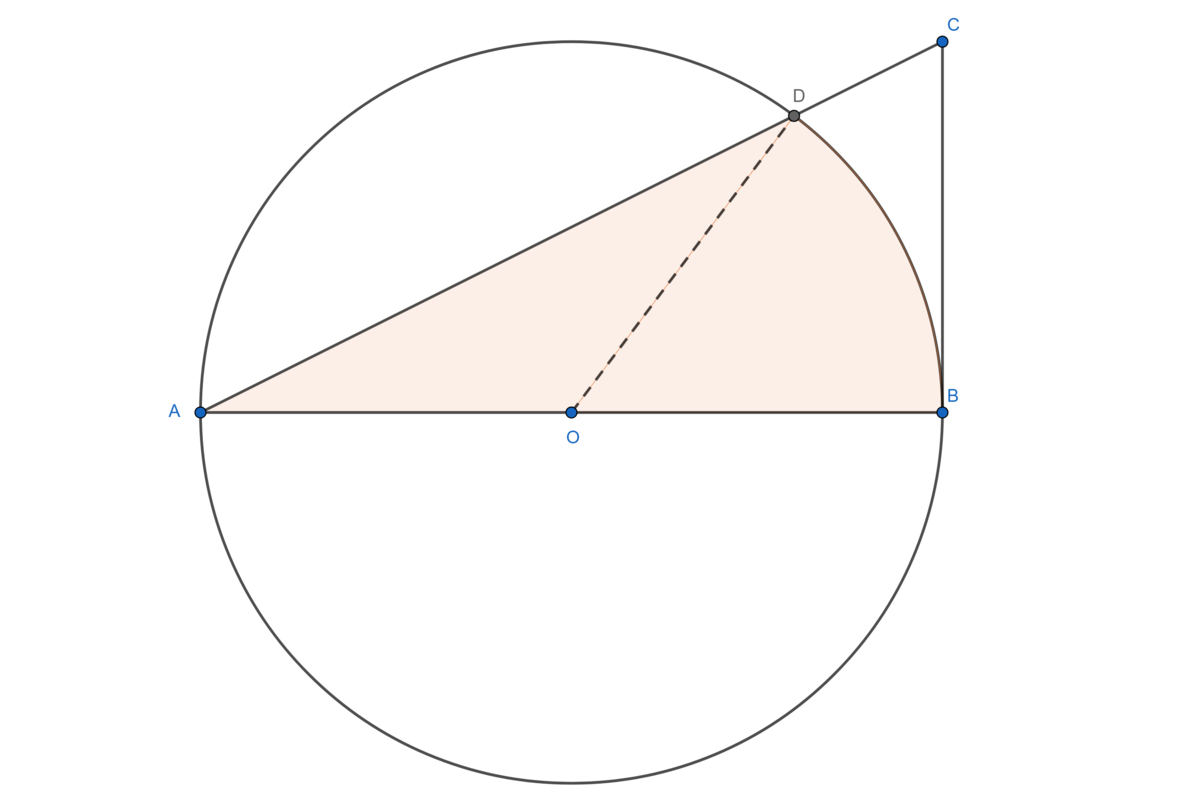Let $O$ be the center of the circle and let $D$ be the intersection of the circle and $\overline{AC}$ . Construct radius $\overline{OD}$ . The area of the shaded region is thus $\mathrm{Area}(\triangle AOD) + \mathrm{Area}(\widehat{BOD})$ where $\widehat{BOD}$ represents the circular sector bounded by $\overline{OB}$ and $\overline{OD}$ .

Simple trigonometry tells us that $\angle BAC = \tan^{-1}\left(\frac{1}{2}\right)$ . Thus $\angle BOC = 2\tan^{-1}\left(\frac{1}{2}\right) = \theta$ . Thus $\mathrm{Area}(\widehat{BOD}) = \frac{\theta}{2\pi}\pi r^2 = \frac{\theta}{2} r^2$ Now, $\angle AOD = \pi - \theta$ . Thus, $\mathrm{Area}(\triangle AOD) = \frac{1}{2} r^2 \sin(\pi - \theta) = \frac{1}{2} r^2 \sin \theta$ Finally, we compute the area of the whole region: $\begin{aligned} A &= \mathrm{Area}(\triangle AOD) + \mathrm{Area}(\widehat{BOD}) \\ &= \frac{1}{2} r^2 \sin \theta + \frac{\theta}{2} r^2 \\ &= \left[\frac{1}{2} (\theta + \sin \theta)\right]r^2 \end{aligned}$ Thus $C=\boxed{\frac{1}{2} (\theta + \sin \theta)}$ .

I did it in the most noob way possible. If $\theta = 45 ^ \circ$ then the resulting area is $\frac {1}{4} {\pi } \ r ^ 2 + \frac {1}{2} \ r ^ 2$ because the area in question is the sum of a half square and a quarter of the circle, just picture it mentally and you ' ll know what I mean. Further, $\frac {1}{4} {\pi } \ r ^ 2 + \frac {1}{2} \ r ^ 2$ = $\frac {1}{2} r ^ 2 ( \frac {1}{2} \pi + 1 )$ = $\frac {1}{2} r ^ 2 ( 2 \theta + \sin (2 \theta))$

The area equals the area of a semi circle reduced by the area of the circular segment between A and D with central angle $\alpha=\pi-2\theta$ :

$A=\frac{r^2\pi}{2} - \frac{r^2}{2}(\alpha-sin\alpha) = \frac{r^2\pi}{2} - \frac{r^2}{2}(\pi-2\theta - sin(2\theta)) = \frac{r^2}{2}(2\theta + sin(2\theta))$

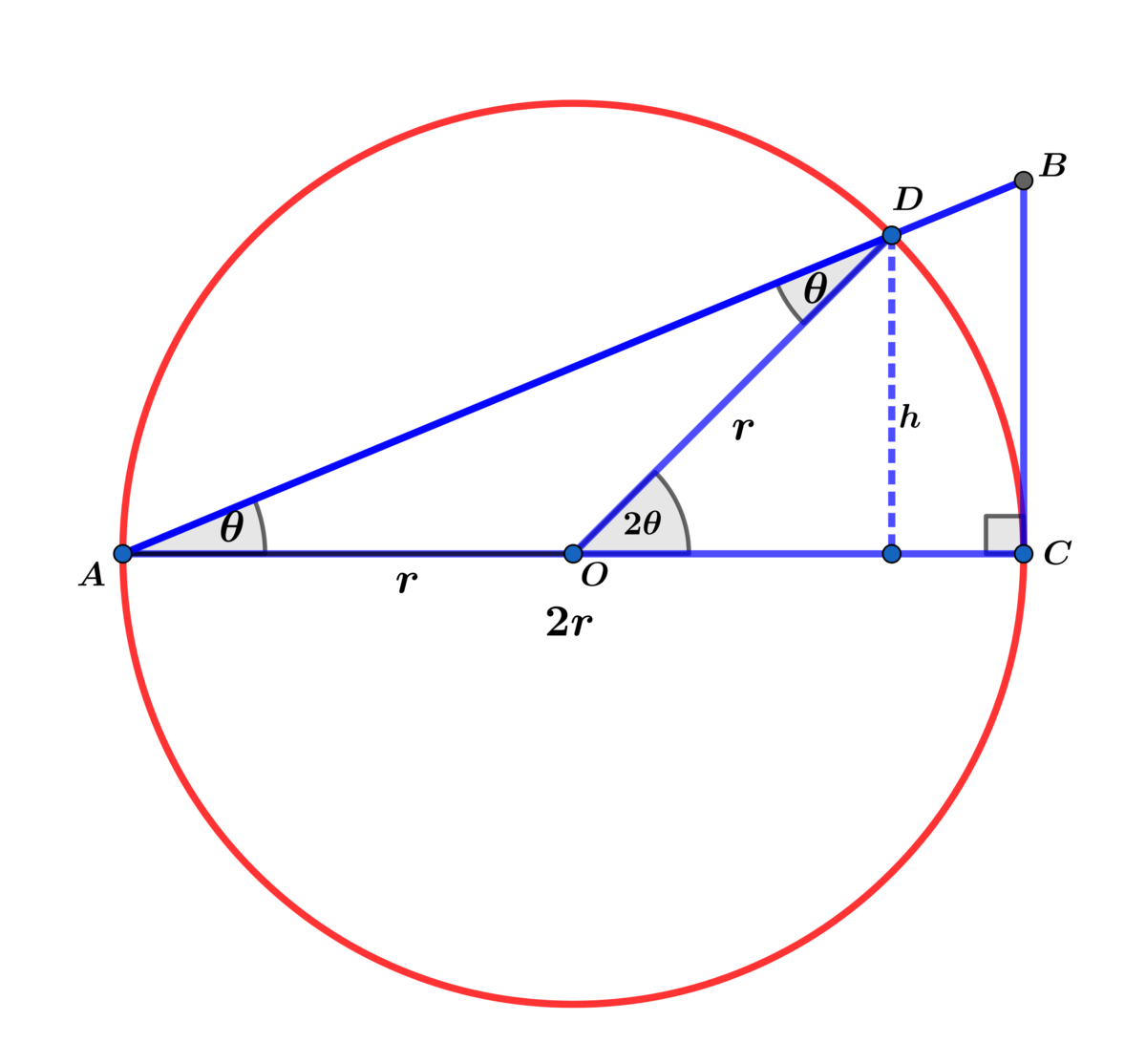
The area of arc $ODC = \dfrac{1}{2}(2\theta)r^2 = \theta r^2$

In $\triangle{AOD}, \:\ h = AD\sin(\theta)$ and $(AD)^2 = 2r^2(1 + \cos(2\theta)) = 4r^2\cos^2(\theta) \implies AD = 2r\cos(\theta) \implies A_{\triangle{AOD}} = \dfrac{1}{2}r^2\sin(2\theta)$

$\implies$ The desired area $A_{T} = r^2(\theta + \dfrac{1}{2}\sin(2\theta)) = \boxed{\dfrac{r^2}{2}(2\theta + \sin(2\theta))}$ .

When angle is pi/2,area should be pi(r) ^2/2

Now... Just pi/2 in the options.... And u will get the correct option.